Transformer模型详解

Transformer

上一节中我们详细介绍了Seq2Seq模型和Attention机制的应用，首先来看即便是带有Attention机制的Seq2Seq模型仍存在的问题。由于不管是Encoder还是Decoder，我们都使用了RNN系列模型，因此梯度问题还是无法避免。在2017年，一篇名为Attention is you need的论文一经发表，就从此掀起了研究Transformer的热潮。在本节，我们就详细的来剖析一下最Vanilla版本的Transformer。

模型总体结构

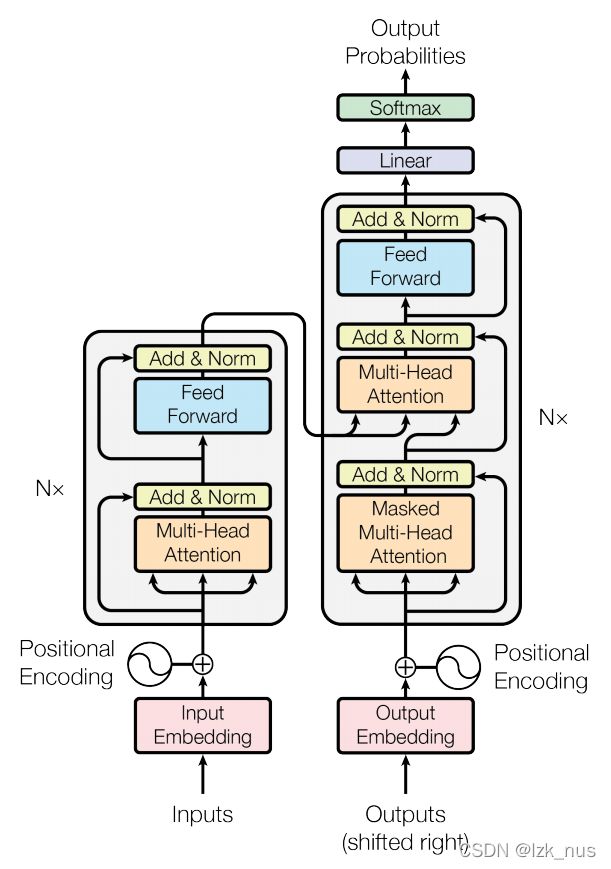
Transformer模型仍然是一个Encoder-Decoder模型，一个Transformer是由多个Encoder Block和多个Decoder Block组成的。

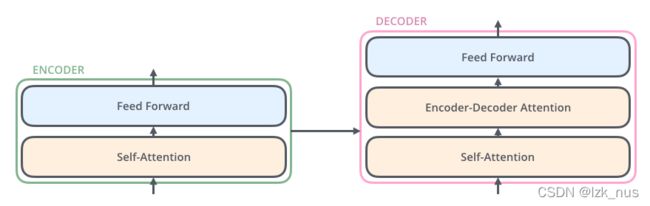
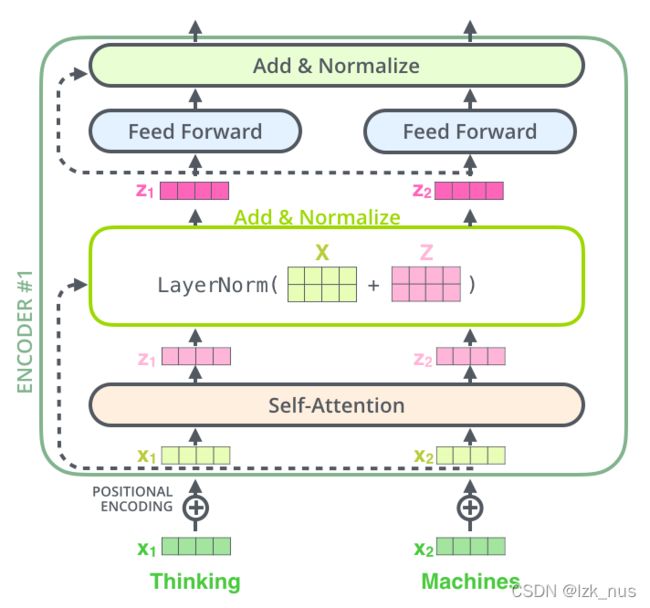
每一个Encoder和Decoder的内部大体结构如下图所示

接下来，我们就分别对这两部分进行剖析。

Encoder

首先来看Encoder的结构

根据这幅简化后的图，我们不难得到Encoder的运行过程：输入原始embedding $x$​，经过一个Self-Attention层得到一个新的表示$z$​，然后再经过一个FFNN得到当前Block的输出。很显然，Encoder中最核心的部分就是Self-Attention的部分了，我们重点来看。

Self-Attention

在Self-Attention模块中，我们引入了这样的三个向量：$(Q,K,V)$。$Q$叫做query，$K$叫做key，$V$叫做value。这三个量是通过以下方式得到的：
$$Q_i=W_q^T{x}_i$$

$$K_i=W_k^T{x}_i$$

$$V_i=W_v^T{x}_i$$

接下来，我们得到了一个句子中每一个token的$(Q,K,V)$。下图以两个单词为例

假如当前时刻为$i$​，我们要计算得到单词$x_i$的输出$z_i$​，那么计算的过程如下：

1. 用$x_i$的query向量$q_i$与句子中每一个单词的key向量$k_j(1\le j\le n)$​进行内积得到一个score向量$[scor{e}_1,scor{e}_2\dots scor{e}_n]$
2. 用得到的score向量除以$\sqrt{d_k}$得到处理后的score向量​，其中$d_k$​是$(q,k,v)$​向量的维度
3. 对处理后的score向量做归一化操作，使用$softmax$函数，得到权重向量${\alpha }_i$​，也就是我们的attention。
4. 用向量${\alpha }_i$和$v_i$得到当前单词$x_i$的新representation，即$z_i={\sum }_{j=1}^n{\alpha }_{ij}{v}_i$

以上就是计算一个单词最终状态$z$的过程，对每个单词都执行上述操作就得到了状态矩阵$Z$​，然后传入FFNN得到当前Block的输出

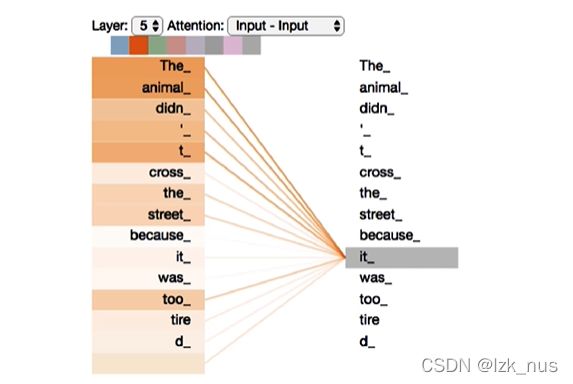
Attention可视化结果

Multi-Head Self-Attention

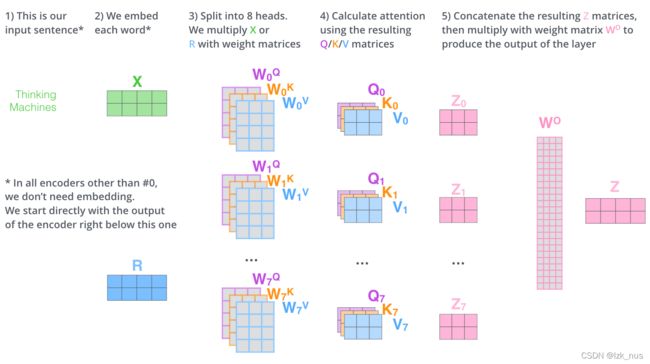
在实际模型中，我们往往使用的是多头Self-Attention，也就是有多组$(Q,K,V)$。

根据上图所示，每一组$(Q,K,V)$​都能得到一个单词的状态，我们把所有单词的所有状态concatenate然后乘一个transpose矩阵得到最终的满足我们需要的shape的状态矩阵。可以结合卷积神经网络来理解一下，每一组$(Q,K,V)$就像是一个卷积核，提取了不同的特征。

Multi-Head Attention可视化结果

Positional Encoding

接下来我们来看一下Transformer模型是怎么考虑单词之间的位置信息，也就是时序信息的。因为我们从Self-Attention的计算方式可以看出，Transformer不是一个时间序列模型，因此对时序特征需要进行特殊处理。原论文中提出的方法叫做位置编码(Positional Encoding)。位置编码采用的是三角函数进行计算，具体公式如下：
$$P{E}_{(pos,2i)}=sin(pos/10000^{2i/d_{model}})$$

$$P{E}_{(pos,2i+1)}=cos(pos/10000^{2i/d_{model}})$$

使用这种公式计算 PE 有以下的好处：

1. 使 PE 能够适应比训练集里面所有句子更长的句子，假设训练集里面最长的句子是有 20 个单词，突然来了一个长度为 21 的句子，则使用公式计算的方法可以计算出第 21 位的 Embedding。
2. 可以让模型容易地计算出相对位置，对于固定长度的间距 $k$，$PE(pos+k)$ 可以用 $PE(pos)$ 计算得到。因为 $\sin (A+B)=\sin (A)\cos (B)+\cos (A)\sin (B)$, $\cos (A+B)=\cos (A)\cos (B)-\sin (A)\sin (B)$。

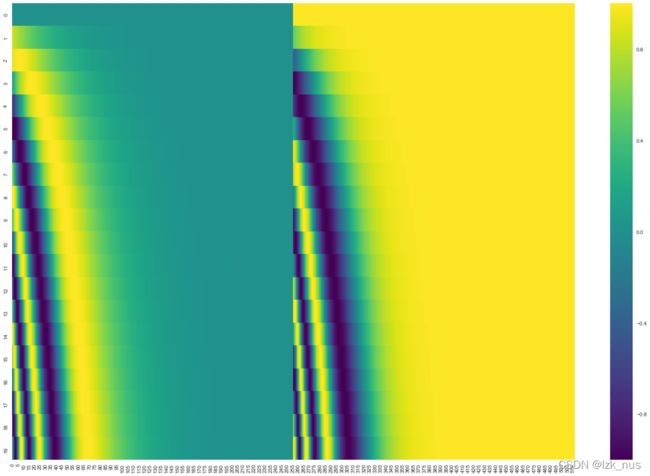
位置编码的效果图如下，每一行是一个词向量的位置编码。

得到每一个词的位置编码向量后，我们将它与原始单词$embedding$相加作为Self-Attention的输入，即
$$x_t=embe{d}_t+po{s}_t$$

Encoder总览

下面给出Encoder准确的模型结构图，我们发现作者在Encoder Block中引入了残差结构，并且在Self-Attention后使用了Layer-Normalization。LayerNorm也是一种标准化方式，与BatchNorm类似，只不过BN是对batch维度求均值和方差(对每一行)，而LN是对样本维度求均值和方差(对每一列)，具体公式如下
$$LayerNorm(x_i)=\alpha \frac{x_i-{\mu }_L}{\sqrt{{\sigma }_L^2+\delta }}+\beta$$

Decoder

介绍完Encoder，接下来说一说Decoder。不说废话先上图

右边便是我们的Decoder。Decoder Block中的内容其实也是一些Self-Attention+Add&Norm+FFNN，唯一的一点小变化是，Decoder中用到了Masked Multi-Head Attention和Encoder-Decoder Attention。

Masked Multi-Head Attention

这里的mask分两种，我们分别来介绍。

Padding Mask

输入的序列长度一般是不一致的，因此我们需要padding。而对于$max\_len$太大的情况，我们一般采取截断，因此我们的attention不应放在截断点右侧多余的信息上。具体的做法是把右边单词的attention设置为负无穷，这样$softmax$后的权重就接近于0.

Sequence Mask

在Decoder解码过程中，我们是不能看到当前时刻$t$之后的信息的，因此在计算attention时需要把$t+1$~$n$时刻的输入给mask掉，也就是使用Sequence Mask。具体做法时是用一个下三角矩阵。

Encoder-Decoder Attention

这个模块是求Decoder经过Masked Multi-Head Attention后的状态和Encoder最终的输出之间的attention，也就是相当于我们Seq2Seq模型中的attention，考虑的是我们翻译当前单词的时候应该去关注源文本哪部分信息。

至此，Transformer的基础理论就介绍完了。Transformer完美的解决了我们文章开头所提到的Seq2Seq模型中的梯度问题，因为我们可以看到，整个Transformer模型在计算的时候没有梯度的积累，Self-Attention只是简单的两两计算，没有什么复杂的梯度计算。Transformer模型在NLP领域的效果非常好，现在也已经被引入到了CV领域。

Summary

Transformer模型的优点如下：

1. 由于attention只涉及矩阵运算，因此可以很好的进行并行运算，充分利用GPU资源
2. 缓解了RNN模型存在的梯度弥散或梯度爆炸等问题
3. Self-Attention可以让模型更好的学习到全局信息

Talk is cheap. Show me the code!