数据结构——红黑树
AVL树可以将查找的效率提升到logN,但是AVL树的插入节点和删除节点,为了维持高度的平衡
需要大量的旋转,而这大量的的旋转,导致非常浪费资源,于是就有人提出了新的一种树——
红黑树,红黑树在牺牲了logN查找效率的的情况下,换做不需要那么多的旋转,转而用“颜色”
来管理二叉树,,也得到了不错的效果,它的查找效率是log2N,也是logN级别的。但是少了
很多旋转
接下来也是只介绍红黑树的插入。
文章目录
- 1.红黑树
-
- 1). 初步认识红黑树
- 2). 红黑树的节点
- 3). 红黑树节点的插入
- 4). 红黑树的变色与旋转
-
- a. 叔叔节点存在且为红
- b. 叔叔节点不存在或者存在为黑
-
- I.叔叔节点不存在
- II.叔叔节点存在且为黑
- 5). 红黑树的验证
1.红黑树
1). 初步认识红黑树
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或
Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路
径会比其他路径长出两倍,因而是接近平衡的。让我们先来看看红黑树:

上面这两颗树都是红黑树。而红黑树主要是以下几种性质,也算规则:
性质1. 结点是红色或黑色。
性质2. 根结点是黑色。
性质3. 所有叶子都是黑色。(叶子是NIL结点)
性质4. 每个红色结点的两个子结点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色结点)
性质5. 从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点。
这其中的NIL节点也可以理解为空指针。
以上五个性质,主要是性质4和性质5导致了 “红黑树确保没有一条路径会比其他路径长出两倍”。为什么呢?其实也很好验证。但在此之前我们需要再次认识“路径”这个问题,现在问你一个问题上图中的第一个红黑树的路径有多少个?不乏有人脱口而出三种,那这种认识就是错误的,正确答案是7种。这里的路径应该是根节点到每个空指针的总和,所以我会在上图画出空指针。为了方便数清路径。
那我们再次回到原来那个问题,为什么红黑树确保没有一条路径会比其他路径长出两倍呢?
性质四说明了父子的颜色关系中只有:黑红、黑黑、红黑、而没有红红
性质五保证了每条路径上的黑色节点数量一样,那么在一种极端情况下,相同黑色节点的路径下最短的路径一定是只有黑色,而最长路径一定是黑红黑红黑红…:
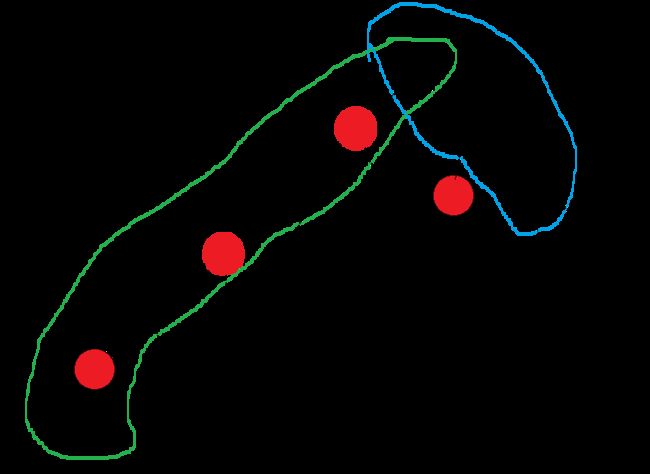
可以看到最左边路径无法再增加节点,为最长路径,最右路径为最短路径,也无法再减少节点。
2). 红黑树的节点
红黑树的节点中有着“颜色”来控制,并且也有指向父亲节点的指针:
enum COLOR{
RED,
BLACK
};
template<class K, class V>
struct RBTreeNode
{
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
pair<K, V> _kv;
COLOR _col;
RBTreeNode(const pair<K, V>& pa)
:_left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _kv(pa)
, _col(RED)
{}
};
3). 红黑树节点的插入
依旧和AVL树一样开始按照二叉搜索树一样的插入:
bool Insert(const pair<K, V>& pa)
{
//插入节点
if (_root == nullptr)
{
_root = new Node(pa);
_root->_col = BLACK;
return true;
}
else
{
Node* cur = _root;
Node* parent = _root;
while (cur)
{
if (cur->_kv.first > pa.first) parent = cur, cur = cur->_left;
else if (cur->_kv.first < pa.first) parent = cur, cur = cur->_right;
else return false;
}
cur = new Node(pa);
if (parent->_kv.first > cur->_kv.first) parent->_left = cur;
else if (parent->_kv.first < cur->_kv.first) parent->_right = cur;
cur->_parent = parent;
cur->_col = RED;
//调整颜色...
return true;
}
}
在上面的代码中我们需要设置新增节点的初始颜色,初始颜色是红色最好,黑色会麻烦很多:
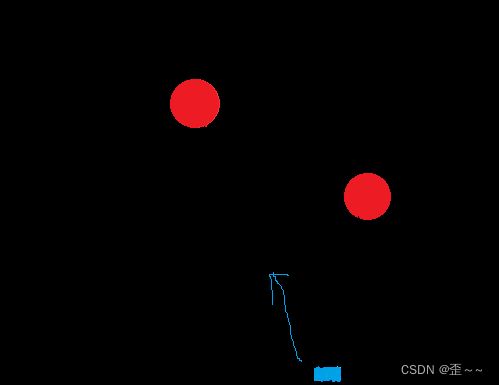
假如我们要在这里新增一个节点,如果我们增加一个红色节点,它没有破坏每条路径的黑色节点数相同,对旁支影响不大。如果是黑色节点,导致其他路径的黑色节点数都要变成三个,影响不小,需要调整整棵树。不止这个节点,任意一个空指针处插入都是如此。因此我们在设置新增节点的需要将新增节点设置为红色。
4). 红黑树的变色与旋转
我们在插入一个新增红色节点的时候,父亲节点只有两种情况,非黑即红,如果父亲节点是黑色的情况,意味着这条路径肯定没有达到最长,而且黑红的父子颜色关系也符合,没有破坏任何规则所以:
新增节红色节点的父亲节点是黑色的情况下不用处理。
那如果父亲节点是红色的话,因为在插入前这棵树一定是一个红黑树,所以此时父亲节点肯定不是根节点,并且父亲节点的父亲也就是新增节点的爷爷节点一定是黑色。而在这种情况下,前人也已经帮我们总结出规律来了,我们只需要跟着演算一下就可以,而这种情况也只需要关注父亲节点的兄弟节点(我们叫它叔叔节点)。
a. 叔叔节点存在且为红
处理方式就是把parent和uncle节点变黑,grandfather变红,cur变成grandfather继续向上调整颜色
因为当把grandfather变红之后你不知道grandfather是不是根节点,也不能确保grandfather的父亲节
点是黑色所以需要迭代调整,知道cur的父亲节点不是红色,而在最后迭代到根节点把根节点变红的
时候,需要将根节点再次变黑。
b. 叔叔节点不存在或者存在为黑
I.叔叔节点不存在
我们先来看叔叔不存在:

一目了然,需要旋转:

然后将parent变黑,grandfather变红,而且也可以看到旋转变色之后不需要继续向上调整,因为新增节点前,跟旋转变色后没有本质的区别。
那么这种呢:

需要一个双旋 + 变色:

同样,这样调整之后也不需要继续向上调整了。
II.叔叔节点存在且为黑
我们再来看叔叔节点存在且为黑的情况:
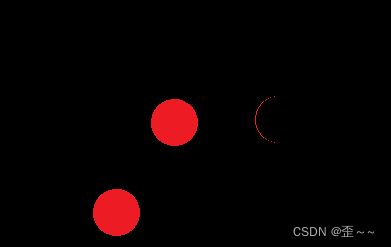
我们发现如果cur它一定是从下面调整上来的,不是新增节点,如果是新增节点的话,parent这颗子树开始是没有新增节点的,也就说明grandfather原来就不是一颗红黑树,这是不合理的。所以我们需要再把这个图画精细一些:

这其中a、b、c是三个节点的子树是一种粗略的,不是具体的某一种树。
而我们将其中一个最简单的情况举例:

而这也只需要一个右单旋 + 变色:
先对grandfather右单旋:

然后就需要变色了,这时我们将那个粗略一点的图也右单旋了:

我们分析这张图,我们可以看到a、b中至少有一个黑色节点,在有多余的黑色节点,则c中也要增加对应的黑色节点数,在上面讨论新增节点的初始颜色时也说到,尽量不要有多余的黑色节点,所以要变化,尽量在变化的过程中不要让路径上的黑色节点多出来。假设cur这颗子树有每条路径有k个黑色节点,那么b中也是同样的情况,而c中每条路径有k-1个黑色节点:

在这种情况下调整颜色的方案就有两种了
1.把cur变黑导致parent每颗子树的的黑色节点数量变成k+1个,但是parent是红色
无法保证parent的父亲节点是黑色,所以需要向上调整。
2.把parent变成黑色,grandfather变成红色,使parent每颗子树上的黑色节点变成k个。
且由于parent是黑色,所以不需要向上调整了。
那么由此观之第二种方法显然更稳定。所以我们选择第二种方式:
把parent变成黑色,grandfather变成红色:

那如果是这种情况呢?

跟上面叔叔节点不存在一样先左旋parent再右旋grandfather,然后再变色

我们再次假设a1中每条路径有k个黑色节点:

那么根据上面的变色规律我们可以得出这里的变色是cur变黑,grandfather变红。也不需要向上调整。
至此所有叔叔在右边的情况就已经说完了,剩下的就是叔叔在左边,与上述对称,不再赘述,直接上代码:
bool Insert(const pair<K, V>& pa)
{
if (_root == nullptr)
{
_root = new Node(pa);
_root->_col = BLACK;
return true;
}
else
{
Node* cur = _root;
Node* parent = _root;
while (cur)
{
if (cur->_kv.first > pa.first) parent = cur, cur = cur->_left;
else if (cur->_kv.first < pa.first) parent = cur, cur = cur->_right;
else return false;
}
cur = new Node(pa);
if (parent->_kv.first > cur->_kv.first) parent->_left = cur;
else if (parent->_kv.first < cur->_kv.first) parent->_right = cur;
cur->_parent = parent;
cur->_col = RED;
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
//右树是叔叔
if (grandfather->_left == parent)
{
Node* uncle = parent->_right;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = grandfather->_parent;
}
else
{
if (parent->_left == cur)
{
RotateR(grandfather);
grandfather->_col = RED;
parent->_col = BLACK;
}
else
{
RotateL(parent);
RotateR(grandfather);
grandfather->_col = RED;
cur->_col = BLACK;
}
break;
}
}
//左树是叔叔
else
{
Node* uncle = parent->_left;
if (uncle && uncle->_col == RED)
{
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = grandfather->_parent;
}
else
{
if (parent->_right == cur)
{
RotateL(grandfather);
grandfather->_col = RED;
parent->_col = BLACK;
}
else
{
RotateR(parent);
RotateL(grandfather);
grandfather->_col = RED;
cur->_col = BLACK;
}
break;
}
}
}
_root->_col = BLACK;
return true;
}
}
5). 红黑树的验证
bool Check(Node* root, int blacknum, const int refVal)
{
if (root == nullptr)
{
if (blacknum != refVal)
{
return false;
}
return true;
}
if (root->_col == RED && root->_parent->_col == RED)
{
return false;
}
if (root->_col == BLACK)
{
++blacknum;
}
return Check(root->_left, blacknum, refVal)
&& Check(root->_right, blacknum, refVal);
}
bool IsBalance()
{
if (_root == nullptr)
return true;
if (_root->_col == RED)
return false;
int refVal = 0;
Node* cur = _root;
while (cur)
{
if (cur->_col == BLACK)
{
++refVal;
}
cur = cur->_left;
}
int blacknum = 0;
return Check(_root, blacknum, refVal);
}
int Height()
{
return _Height(_root);
}
int _Height(Node* root)
{
if (root == nullptr)
return 0;
int leftHeight = _Height(root->_left);
int rightHeight = _Height(root->_right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
size_t Size()
{
return _Size(_root);
}
size_t _Size(Node* root)
{
if (root == NULL)
return 0;
return _Size(root->_left)
+ _Size(root->_right) + 1;
}

