数据结构-树

part7 树

0-前言

之前我们一直在谈的是一对一的数据结构。可现实中，还有很多一对多的情况需要处理，所以我们需要研究这种一对多的数据结构——“树”，考虑它的各种特性，来解决我们在编程中碰到的相关问题。

在操作系统中，用树来表示文件目录的组织结构。

在 编译系统中，用树来表示源程序的语法结构。

重点：二叉树的存储结构和各种操作。

 

1-定义

1.1 定义

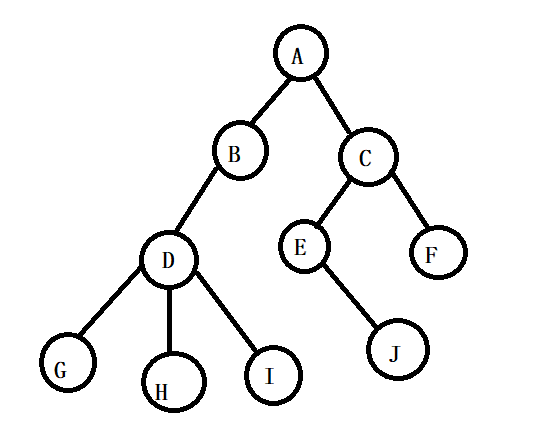
树（tree）是n（n>=0）个结点的有限集。

n=0时：称为空树。

n>=0时：在任意一颗非空树中：

 （1）有且仅有一个特定的称为根的结点。
 （2）当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1、T2、······、Tm,其中每个集合本身又是一棵树，并且称为根的子树（sub_tree）

子树T1和子树T2就是根节点A的子树

当然D、G、H、I组成的树又是B为根节点的子树，E,J组成的树是以C为根结点的子树。

对于树的定义还需要强调：

 n=0时: 空树，没有根节点
 n>0时: 根节点是唯一的，不可能存在多个根节点。
 m>0:子树的个数没有限制，但它们一定是互不相交的。

如下图，该结构不符合树的定义，因为它们有相交的子树。

 

1.2 表示

1.2.1 集合表示法

1.2.2 广义表的形式

 A((B(E(K,L),F),C(H(M),J,I),D(G)));
 根作为子树森林组成的表的名字在表的左边。

1.2.3 凹入表示法

1.3 基本术语

结点：树中的一个独立单元，包含一个数据元素及若干指向其子树的分支。

度： 结点拥有的子树数

叶子： 度为0的结点（又称终端结点）

分支结点：度不为0的结点（又称非终端结点）。除根节点之外，分支结点也称为内部结点。

树的度:是树内各结点的度的最大值。

 这棵树结点的度最大值是结点D的度，为3，所以树的度也为3.

1.4 结点关系

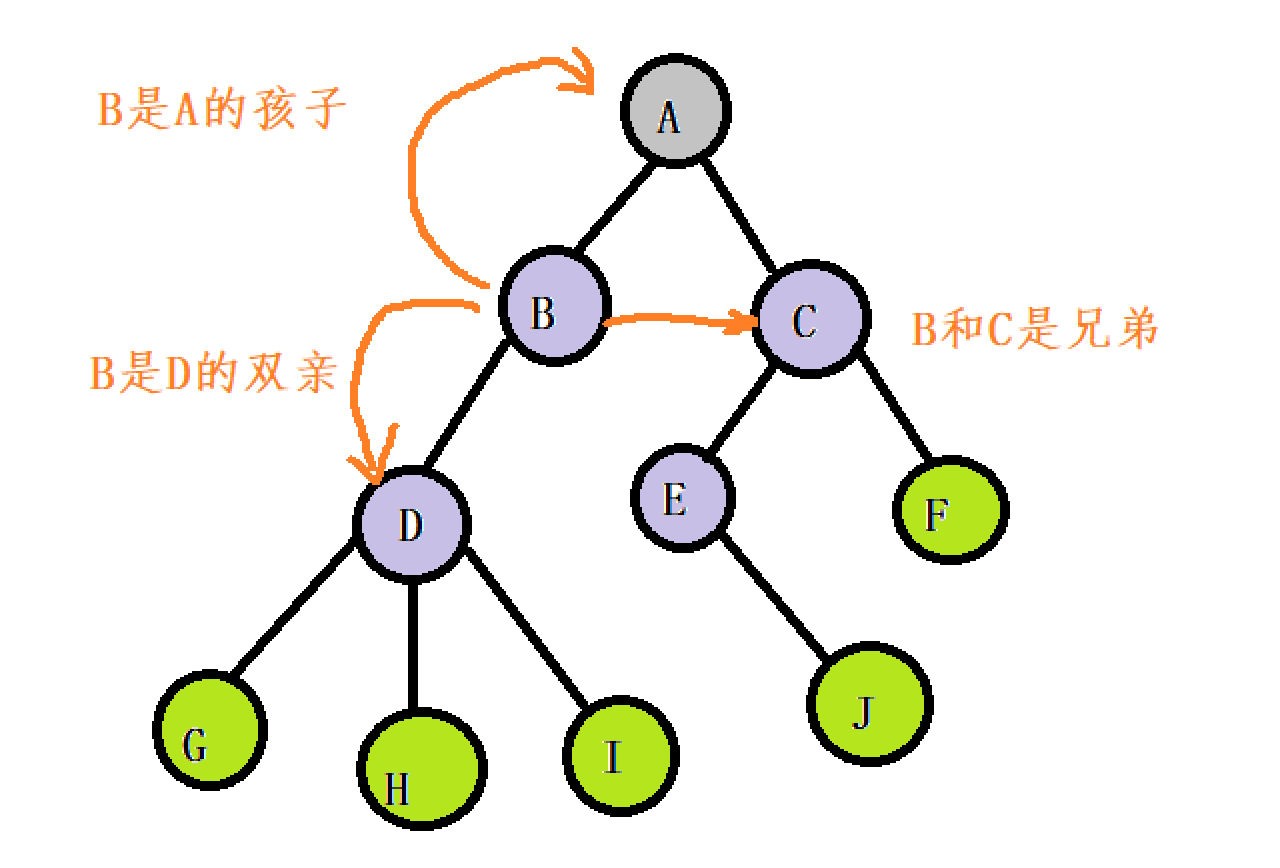
结点的子树的根称为该结点的孩子

相应的，该结点称为孩子的双亲。

同一个双亲的孩子之间互称兄弟。

结点的祖先：是从根到该结点所经分支上的所有结点

子孙：以某 结点为根的子树中，任一结点都称为该 结点的子孙。如

 对于H来说，D、B、A都是它的祖先
 对C来说，E,F,J都是它的子孙

1.5 树的层次

结点的层次从根开始定义起，根为第一层。根的孩子在第二层。

树中任一结点 的层次等于其双亲结点的层次加一。

双亲在同一层的结点互为堂兄弟。（I,J互为堂兄弟）

树中结点的最大层次称为树的深度或高度，当前树的深度为4

如果将树中结点的各子树看成从左至右是有次序的，不能互换的，则称该树是有序树，否则称为无序树。

森林是m棵互不相交的树的集合。对于树中每个结点而言，其子树的集合即为森林。如下图：

 

对比线性表和树

线性结构	树结构
第一个元素：无前驱	根结点：无双亲，唯一
最后一个元素：无后继	叶节点：无孩子，可以多个
中间元素：一个前驱一个后继	中间结点：一个双亲多个孩子

2 二叉树

2.1 定义

二叉树是n（n>=0）个结点所构成的集合。它或为空树（n=0）;或为非空树。

对于非空树T：

 （1）有且仅有一个称之为根的结点
 （2）除根节点外，其余结点分为两个互不相交的子集T1和T2，分别称为T的左子树和右子树，且 T1和T2本身又都是二叉树。

2.2 区别

二叉树和 树一样具有递归性质,二叉树与树的区别 主要有 一下两点：

（1）二叉树每个结点至多只有两棵子树（即二叉树不存在度大于2的结点）；

（2）二叉树的子树有左右之分，其次序不能任意颠倒。

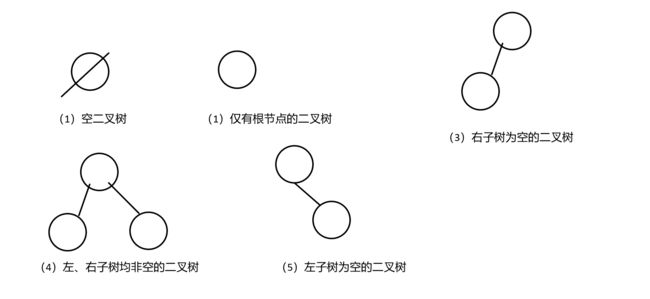
2.3 基本形态

5种基本形态，如下图所示

 

3 表达式(略)

 

（1）若表达式 为数或者简单变量，则相应二叉树中仅有一个根节点，其数据域存放该表达式 信息 。

（2）若表达式为第一操作数， 运算符 第二操作数 的形式，则相应二叉树中，以左子树表示第一操作数，右子树表示 第二操作数，根结点的 数据域存放运算符。

若为单目运算符，则 左子树为空，其中操作数本身又为表达式

如下图所示 a+b*(c-d)-e/f

 

4 二叉树的性质

4.1 性质1：

在二叉树的第i层上最多 有​ 个结点（i>=1）

归纳法可得;

 i=1时，只有一个根节点  2^(i-1) =1
 i>1时  第i-1层上最多有2^(i-2)个结点  每个结点最多有2个孩子结点，
     则第i层上最多有 2^(i-1)*2个结点，即2^(i-1)个。

4.2 性质2：

深度为k的二叉树 至多有​个结点（k>=1）

由性质1得总结点数为

第层最大结点数​

类比二进制表示法：每一位都是1,有k位 其值为​

4.3 性质3

对任何一颗二叉树T，如果其终端结点数为​, 度为2的结点数为​,则​

证明：

步骤1：

设​为二叉树中度为1的结点数 。因为二叉树中所有结点的度均小于或等于 2，所以其结点总数为

步骤2：二叉树中每个结点都有唯一的双亲结点，除了根节点外。设分支数为B

这些分支都是由度为1或者2的结点射出

由式（3）和式（1）相减得

即

5 二叉树的形态

5.1 满二叉树

深度为k,且含有​个结点的二叉树。

5.2 特点

每一层上的结点数都是最大结点数，即每一层（i）的结点数都是​

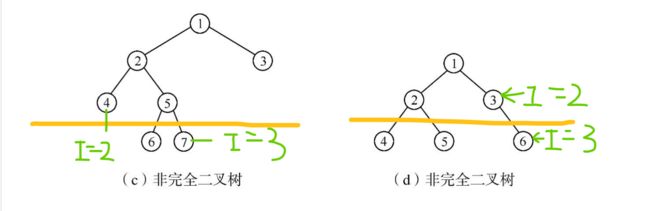
6 完全二叉树

对满二叉树进行连续编号，约定编号从根节点起，自上而下，自左向右。

6.1 特点

（1）叶子结点只可能在最下两层上出现

（2）最下层的叶子一定集中在 左部连续位置

（3）倒数第二层，若有叶子结点，一定都在右部连续位置

（4）如果结点度为1，则该结点只有左孩子，即不存在只有右子树的情况。

（5）同样结点树的二叉树，完全二叉树的深度最小。

如下图所示：

6.2 完全二叉树

6.3 非完全二叉树

如图：(c) 和 （d）

小妙招：按照满二叉树的结构逐层编号，如果编号出现空档，就说明不是完全二叉树 。

7 二叉树的存储

7.1 顺序存储结构

 #define MAXSIZE  100//二叉树的最大结点数
 ​
 typedef int  elem_type;
 typedef elem_type  sq_bi_tree[MAXSIZE];// 0号单元 存储根节点
 sq_bi_tree   bt;

顺序存储结构使用一组地址连续的存储单元来存储数据元素，为了能够在存储结构中反应结点之间的逻辑关系，必须将二叉树中的结点按照一定的规律安排在这组单元中。

7.2 完全二叉树

只要从根起，按层序存储即可，按照自上而下，自左向右存储结点元素。

即将完全二叉树上编号为i的结点存储在如上定义的一维数组中下标为i-1的元素中。

对于一般二叉树，则将其每个结点与完全二叉树上的结点相对照，存储在一维数组的对应元素中，

考虑最坏情况，一个深度为k且只有k个结点的单支树（斜树），需要长度为​的一维数组

（二叉树的性质1）

故而，顺序存储结构仅适用于完全二叉树。

7.3 链式存储

对于一般二叉树，更适合采用链式存储结构。

由二叉树的定义得知，二叉树的结点由数据元素+指向左子树的分支+指向右子树的分支

7.3.1 结点示意图

 

结构（b）称为二叉链表

结构（c）称为三叉链表

7.3.2 逻辑示意图

规律：含有n个结点 的 二叉链表中有n+1个空链域

8 二叉树的遍历

8.1 结点定义

typedef   int  elem_type;
typedef   struct bi_node
{
	elem_type  data;//结点数据域
	struct bi_node *lchild,*rchild;//左右孩子指针。
}bi_node,*bi_tree;

8.2 遍历算法

8.2.1 概念

按照某种次序访问树的每个结点，使得每个结点均被访问一次。而且仅被访问一次。

访问：输出结点信息 ，对结点进行运算，对结点信息进行修改等

8.2.2 实质

遍历的实质是对二叉树进行线性化的过程。

即遍历的结果是将非线性结构的树中结点排成一个线性序列。

根据二叉树的递归特性可得：

二叉树有三个基本单元：根节点（D），左子树(L)和右子树(D)

若依次遍历 这三个部分，便遍历了整个二叉树。则有DLR,DRL,LDR,LRD,RDL,RLD这6种遍历方案。

若限定先左后右，则仅有DLR, LDR, LRD三种情况，分别称为 先（根）序遍历，中（根）序遍历，后（根）序遍历。

8.3 先序遍历

8.3.1 算法描述

若二叉树为空，则空操作
若非空：DLR
（1）访问根节点
（2）先序遍历左子树
（3）先序遍历右子树

表达式（a+b*(c-d)-e/f）

8.3.2 示意图

 

8.3.3 表达式的前缀表示：（波兰式）

8.3.4 递归算法---DLR

void  pre_order_traverse(bi_tree t)//根节点
{
	if(t==null)
	  return ;
	  printf("%c",t->data);//显示结点信息
	  pre_order_traverse(t->lchild);//先序遍历左子树
	  pre_order_traverse(t->rchild);//先序遍历右子树
}

8.4 中序遍历

8.4 1 算法步骤

（1）中序遍历左子树
（2）访问根节点
（3）中序遍历右子树

8.4.2 遍历流程示意图

 

 

8.4.3 表达式中缀表示

8.4.4 递归算法---LDR

中序遍历

void   in_order_traverse(bi_tree t)
{
	if(T==NULL)
		return;
	in_order_traverse(t->lchild);//中序遍历左子树
	//压栈到左叶子结点，逐一出栈（后进先出）
	printf("%c",t->data);//
	in_order_traverse(t->rchild);//中序遍历右子树
}

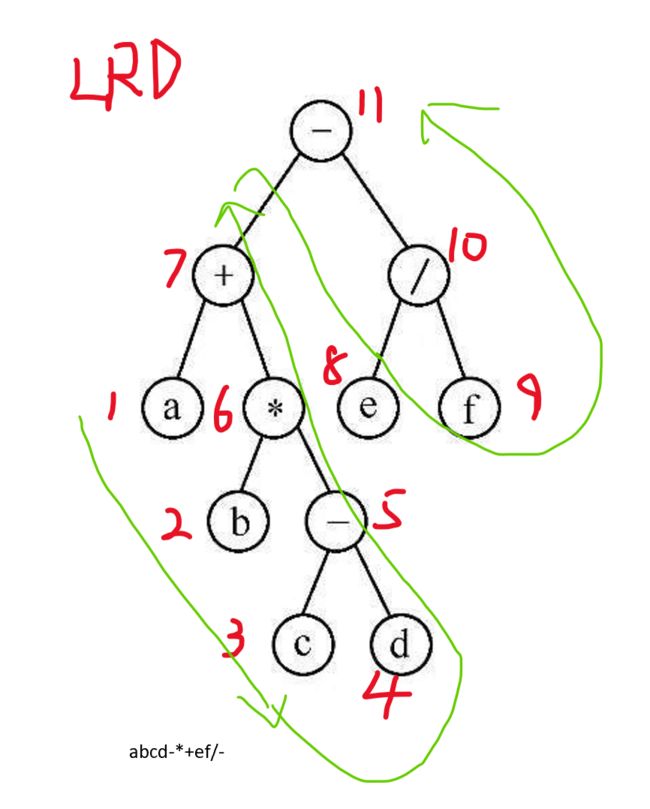
8.5 后序遍历LRD

8.5.1 后序遍历算法

（1）后序遍历左子树
（2）后序遍历右子树
（3）访问根节点

8.5.2 访问流程示意图

 

8.5.3 逆波兰式

8.5.4 递归算法---LRD

void  post_order_traverse(bi_tree t)
{
	if(t==NULL)
	     return ;
	post_order_traverse(t->lchild);//后序遍历左子树 
	post_order_traverse(t->rchild);//后续遍历右子树
	printf("%c",t->data);//显示结点数据
}

 

 

8.6 非递归算法

8.6.1 算法步骤

中序遍历示例：

（1）初始化一个空栈s，指针p指向 根节点
（2）申请一个结点空间 q,用来存放栈顶弹出的元素
（3）当p非空或者栈 s非空时，循环执行下列操作
  		·如果p非空，则将p进栈，p指向该结点的左孩子
  		·如果p为空，则弹出栈顶元素并访问，将 p指向该结点的右孩子

 

8.6.2 算法实现

void in_order_traverse(bi_tree t)
{
	init_stack( &s );
	bi_tree p=t;
	while(p||!stack_empty(s))
	{
		if(p)//非空
		{
			push(s,p);//压栈
			p=p->lchild;
		}
		else
		{
			pop(s,q);//出栈
			p=p->rchild;
		}
	}
}

 

8.7 非层次遍历

按照从上到下，从左到右的顺序遍历二叉树。层次遍历不是递归过程，可以 借助队列实现

 

8.8 推导遍历结果

 

9 二叉树的建立

9.1 扩展二叉树

假设我们要建立如下左图的二叉树。采用先序遍历得到ABDC

为了确定每个结点的左右结点，可以对其进行拓展，则先序遍历得到AB#D##C##

9.2 算法步骤

（1）扫描字符序列，读入字符ch
（2）如果ch是一个'#'字符，则表明该二叉树 为空树，则t为NULL,否则执行 一下操作
	·申请一个结点空间t;
	·将ch赋给t->data;
	·递归创建t的左子树
	`递归创建t的右子树

9.3 算法实现

 

 

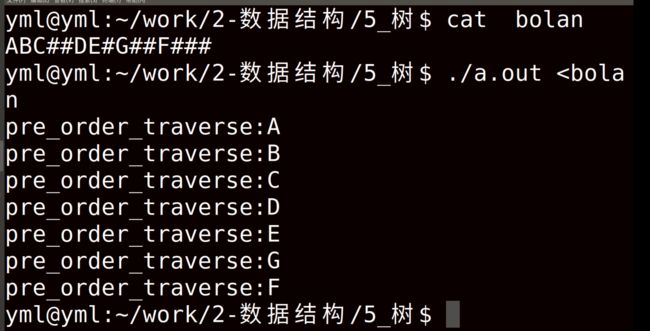
（a）ABCD#####
（b）ABC##DE#G##F###(最后一个#是A的右节点)

输出结果️

输出结果️

 

10 统计结点个数

10.1 算法分析

空树：结点为0；
非空树:
结点总数=左子树的结点个数+右子树的结点个数+根节点数

 

类比：
楼梯有n阶台阶，上楼可以一步上1阶，也可以一步上2阶，编程序计算n阶台阶共有多少种不同的走法
提示：n阶台阶走法可以分成两种情况：
	n-1阶走法+1阶
	n-2阶走法+2阶

10.2 代码实现

int  node_num(bi_tree t)
{
	if(t==NULL)
		return 0;
	else
		return node_num(t->lchild)+node_num(t->rchild);
}

 

11树的应用---最优树

 

哈夫曼树又称最优树

11.1 成绩评价系统

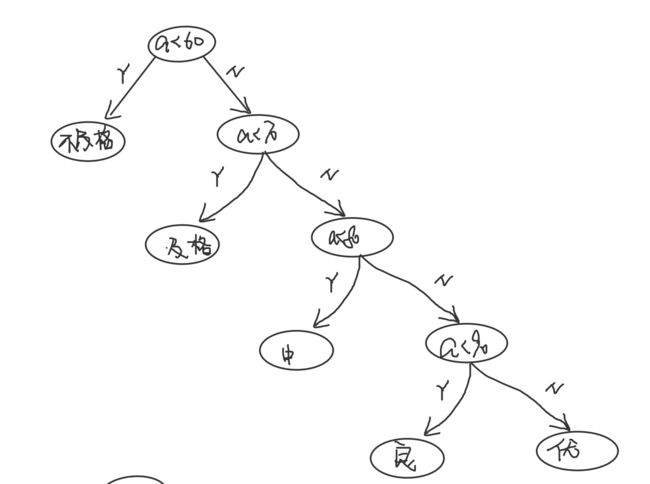
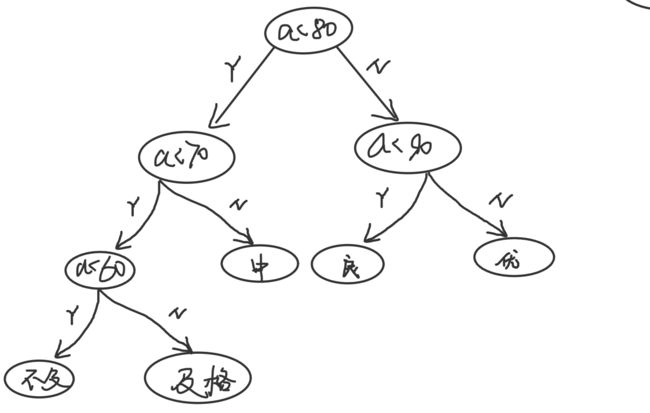
11.1.1 示例

获取学生的成绩，进行等级评价

char score;
score=getchar();
if(s<60)
	printf("F\n");
else if(a<70)
	printf("D\n");
else if(a<80)
	printf("C\n");
else if(a<90)
	printf("B\n");
else if(a<=100)
	printf("A\n");

11.1.2 流程图

 

11.1.3 概率问题

学生成绩近似符合正态分布

分数	0-59	60-69	70-79	80-89	90-100
比例	5%	15%	40%	30%	10%

由此：70分以上占比80%，70分以上的成绩需要经过至少 3次以上的判断才能得到结果。程序效率不高。

11.2 算法优化

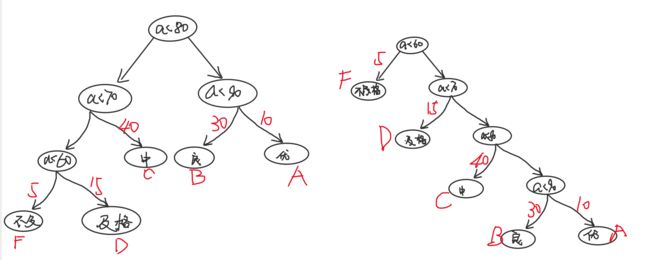
仔细观察发现，中等成绩（70-79）比例最高，其次是良好成绩，不及格比例最低

，将该二叉树重新分配

从图中感觉，效率应该高了一些，到底高出多少呢？这样的二叉树如何设计？

11.3 带权路径长度WPL

路径：从树中一个结点到另一个结点之间的分支构成两个结点之间的路径

路径长度: 路径上的分支数目称作路径长度

树的路径长度： 从树根到每个结点的路径长度之和

带权路径长度：该结点到树根之间的路径长度与结点上权的乘积

树的带权路径长度：树中所有叶子结点的带权路径长度之和

哈夫曼树：树的带权路径长度最小的二叉树称作哈夫曼树，也称最优二叉树

分别计算上述两颗树的W(weight)P(path)L(length)值：

左=5*3+15*3+ 40 *2 + 30*2 +10*2 =220
右=5*1+15*2+ 40*3 +30*4 +10*4 =315

这意味着：如果有一万个学生的百分制成绩需要计算五级分制成绩，用左边的二叉树只需要22万次比较，而右边的需要315*10000/100=31500次比较。

 

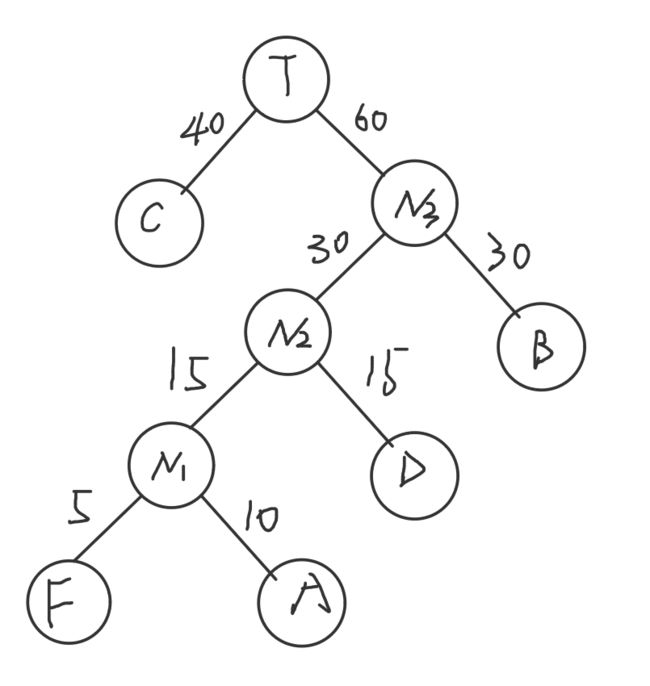
11.4 构造哈夫曼树

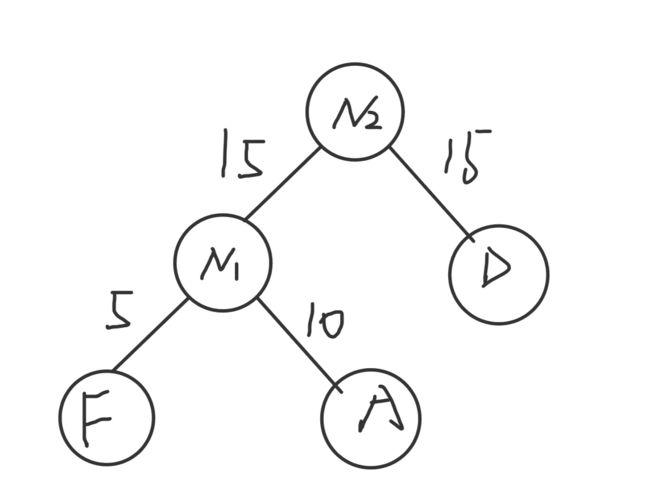
（1）先把有权值的叶子结点按照从小到大的顺序排列
	F5   A10  D15    B30     C40
（2）取最小的两个结点作为新结点N1的两个子结点，注意相对较小的是左孩子。

（3）将N1作为新结点，替换F5  和 A10插入有序序列中
N1的权=5+10=15
N115    D15    B30     C40

（4）将N2作为新结点，替换F A D 插入有序序列
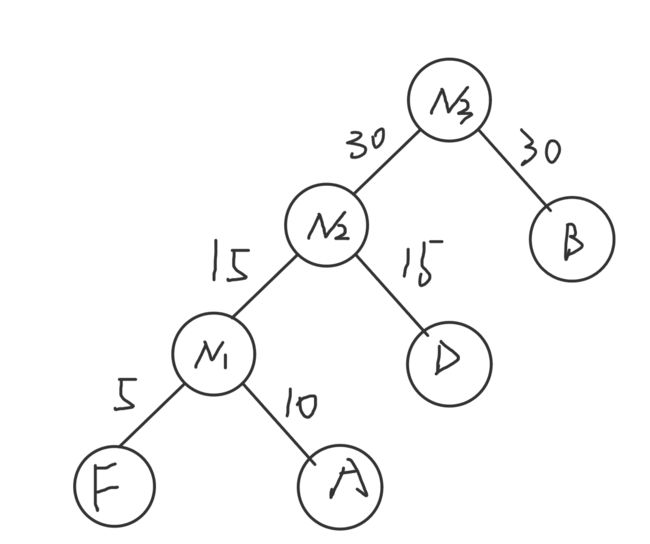
N2=15+15=30
N230     B30     C40

(5)将N3作为新结点，
N3=30+30=60
C40     N360

带权路径长度为：5*4+ 10*4 +15*3 +30*2 +40*1=205  

但是现实总是比理想要更加复杂，由于c要判断的是70-79(a<80 && a>70)，需要两次比较，才能得到yes 或者no ，所以最优解依旧是带权路径长度为220的树。

我们这里重点学习哈夫曼树的构造，不过分讨论其他因素。

12 哈夫曼编码

12.1 数据压缩

随着大数据时代的到来，如何采用 有效的数据压缩技术，来节省数据文件的 存储空间和网络传输时间 越来越引起人们的重视。

在数据通信种，需要将数据 文件转换成由二进制字符0，1组成的二进制串，称为编码。

假设待压缩的数据为“abcd abcd aaaa abbb dd”,文件中只包含a,b,c,d四种字符。

12.1.1 等长编码

如果采用等长编码方案 ，每个字符取两位即可，上述18个字符，编码总长度为36位

12.1.2 不等长编码1

如果考虑字符出现的频率，频率低的字符采用长编码，频率高的字符采用短编码。
a出现7次（7），b出现5次（10），c出现2次（6），d出现4次（12），编码长度为 35

12.1.3不等长编码2

设计不合理的编码会造成解码困难，如方案c
数据编码后：
	001010111·····
	前四个字符可以解码为0 +010   ac
					0+01+0    aba

12.2 小结

不等长编码：任何一个字符的编码都不是另一个字符编码的前缀。

12.3 哈夫曼树

那么如何设计有效的数据压缩的二进制编码呢？

13 总结

概念：子树，结点，度，叶子，分支结点，双亲，孩子，层次，深度，森林

二叉树：满二叉树，完全二叉树（顺序存储结构），一般二叉树（链式存储结构）

二叉树遍历：前序，中序，后序

二叉树建立：递归（并非一定要用到递归，只是递归实现更简洁优雅）

哈夫曼树--最优树

哈夫曼编码----数据压缩原理

 

图片来源：百度图片，手绘，各大电子书截图。