力扣刷题篇之栈与队列2

系列文章目录

---

目录

系列文章目录

前言

一、最小/大栈

二、字符串去重问题

三、栈与括号匹配

总结

---

前言

本系列是个人力扣刷题汇总，本文是栈与队列。刷题顺序按照[力扣刷题攻略] Re：从零开始的力扣刷题生活 - 力扣（LeetCode）

---

一、最小/大栈

面试题 03.02. 栈的最小值 - 力扣（LeetCode）

LCR 147. 最小栈 - 力扣（LeetCode）

加一个最小栈，不断更新最小栈，把最小的不断放在栈顶。

pop()时记得两个栈都要pop()更新。

class MinStack {

    Deque xStack, minStack;


    /** initialize your data structure here. */
    public MinStack() {
        xStack = new LinkedList<>();
        minStack = new LinkedList<>();
        minStack.push(Integer.MAX_VALUE);
    }
    
    public void push(int x) {
        xStack.push(x);
        minStack.push(Math.min(minStack.peek(), x));
    }
    
    public void pop() {
        xStack.pop();
        minStack.pop();
    }
    
    public int top() {
        return xStack.peek();
    }
    
    public int getMin() {
        return minStack.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

155. 最小栈 - 力扣（LeetCode）

方法一： 

这里用到了面向对象

使用 this.node 通常发生在面向对象编程（Object-Oriented Programming，OOP）的场景中，其中 this 表示当前对象的引用，而 node 是该对象的一个成员变量。

使用 this.node 的目的是为了明确指示正在操作对象的实例变量，以避免与方法参数或局部变量发生混淆。在实践中，这有助于提高代码的可读性和维护性。 

class MinStack {
    Node node; // 定义一个节点类型的成员变量node，表示栈顶节点

    public MinStack() {
        this.node = new Node(); // 在构造函数中初始化一个空节点作为初始栈顶
    }

    public void push(int val) {
        Node node = new Node(this.node, val, Math.min(val, this.node.minVal));
        // 创建一个新节点，将新节点的next指向当前栈顶节点，minVal更新为当前节点的最小值与新节点值的较小者
        this.node = node; // 将新节点设置为栈顶节点
    }

    public void pop() {
        this.node = this.node.next; // 将栈顶指针指向下一个节点，即删除栈顶节点
    }

    public int top() {
        return this.node.getVal(); // 返回栈顶节点的值
    }

    public int getMin() {
        return this.node.getMinVal(); // 返回栈中的最小元素值
    }

    private static class Node { // 定义一个内部类Node表示栈的节点
        Node next; // 下一个节点的引用
        Integer val; // 节点的值
        int minVal = Integer.MAX_VALUE; // 当前栈中的最小值，默认为最大整数值

        public Node(Node next, int val, int minVal) {
            this.next = next;
            this.val = val;
            this.minVal = minVal;
        }

        public Node() {
        }

        public Node getNext() {
            return next;
        }

        public void setNext(Node next) {
            this.next = next;
        }

        public int getVal() {
            return val;
        }

        public void setVal(int val) {
            this.val = val;
        }

        public int getMinVal() {
            return minVal;
        }

        public void setMinVal(int minVal) {
            this.minVal = minVal;
        }
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(val);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

 

方法二： 

 这个用数组做的，感觉也不错，好理解

用top和min两个指针分别指向栈顶和最小值，如果数据有更改，两个指针及时更新。

注意，这里有个判断最小值指针是否合法的部分，重新遍历数组找最小值。

class MinStack {

   private  int[] stack;
   private  int top; // 栈顶
   private int min; //最小值指针
   
   public MinStack() {
       this.stack = new int[30000];
       this.top = -1;
       this.min = -1;
   }
   
   public void push(int val) {
       //压栈
       this.stack[++top] = val;
       
       if(min == -1){//判断是否是第一个元素
           min = top;
       }else{
           if(stack[min] > val){ //比较大小
               min = top;  //更新指针
           }
       }
   }
   
   public void pop() {
       top --; //出栈
       if(top == -1){//判断栈是否为空
           min = -1;
       }else if(min > top){//判断最小值指针是否合法
           
           long min_val = Long.MAX_VALUE;
           for(int i = 0;i<= top;i++){//重新找最小
               if(min_val > stack[i]){
                   min_val = stack[i];
                   min = i;
               }
           }
       }
   }
   
   public int top() {
       return stack[top];
   }
   
   public int getMin() {
       return stack[min];
   }
} 

 

716. 最大栈 - 力扣（LeetCode）

等买会员再做。

二、字符串去重问题

316. 去除重复字母 - 力扣（LeetCode）

1081. 不同字符的最小子序列 - 力扣（LeetCode）

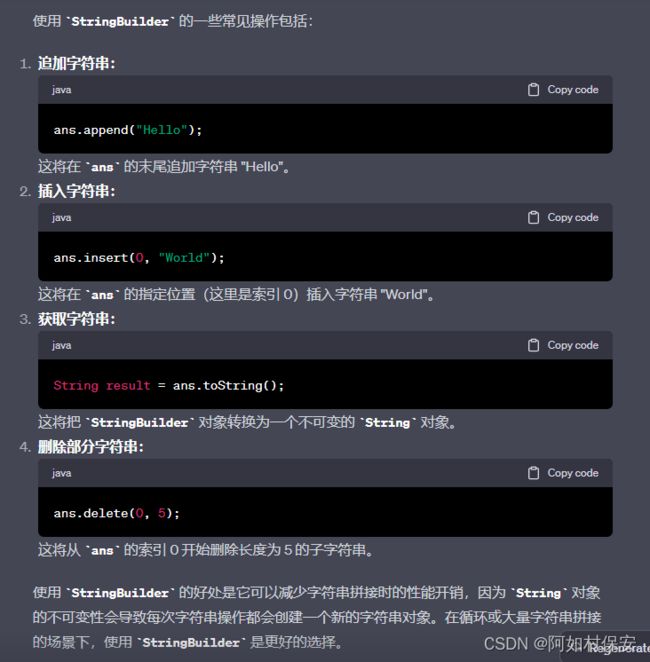
StringBuilder 是 Java 中用于处理字符串的一个类，它允许在一个可变的字符序列中进行高效的操作，而不像 String 对象那样是不可变的。

StringBuilder ans = new StringBuilder(); 创建了一个名为 ans 的 StringBuilder 对象。这个对象可以用来进行字符串的动态构建，特别是在需要频繁地进行字符串拼接操作时，使用 StringBuilder 通常比直接使用 String 更高效。

这个代码太妙了，动态更新， 检查并删除结果字符串中比当前字符大且后面还会出现的字符。

class Solution {
    public String removeDuplicateLetters(String s) {
        // 用于记录每个字符在字符串中出现的次数
        int[] dic = new int[30];
        
        // 将输入字符串转换为字符数组
        char[] arr = s.toCharArray();
        
        // 用于构建最终结果的字符串
        StringBuilder ans = new StringBuilder();
        
        // 用于标记字符是否已经在结果字符串中
        boolean[] inAns = new boolean[26];
        
        // 统计每个字符出现的次数
        for (char c : arr) {
            dic[c - 'a']++;
        }
        
        // 遍历字符数组
        for (char c : arr) {
            int index = c - 'a';
            dic[index]--;
            
            // 如果字符已经在结果字符串中，则跳过
            if (inAns[index]) continue;
            
            // 检查并删除结果字符串中比当前字符大且后面还会出现的字符
            while (!ans.isEmpty() && c < ans.charAt(ans.length() - 1) && dic[ans.charAt(ans.length() - 1) - 'a'] > 0) {
                // 将字符标记为不在结果字符串中
                inAns[ans.charAt(ans.length() - 1) - 'a'] = false;
                
                // 删除结果字符串中的字符
                ans.deleteCharAt(ans.length() - 1);
            }
            
            // 将当前字符添加到结果字符串末尾
            ans.append(c);
            
            // 标记当前字符在结果字符串中
            inAns[c - 'a'] = true;
        }
        
        // 将最终结果转换为字符串并返回
        return ans.toString();
    }
}

 1209. 删除字符串中的所有相邻重复项 II - 力扣（LeetCode）

这个也很牛，直接在新建的数组stack里面原地删减，不断更新索引。最后返回stack数组中从0开始i个元素构成的字符串。

class Solution {
    public String removeDuplicates(String s, int k) {
        int i = 0, n = s.length(), count[] = new int[n];
        char[] stack = s.toCharArray();
        for (int j = 0; j < n; ++j, ++i) {
            stack[i] = stack[j];
            count[i] = i > 0 && stack[i - 1] == stack[j] ? count[i - 1] + 1 : 1;
            if (count[i] == k) i -= k;
        }
        return new String(stack, 0, i);
    }
}

三、栈与括号匹配

20. 有效的括号 - 力扣（LeetCode）

 用数组stack存放各个符号的左半边，然后如果是右边，就要判断和索引对应元素，也就是左边是不是对应的一对符号，如果是就索引减一，相当于删去左边这个已经成对的半边了，如果不是，那么就直接返回FALSE。

class Solution {

    // 下标从-1开始，方便设置新的value 还有查看
    public boolean isValid(String s) {
        char[] stack = new char[s.length()];
        int index = -1;
        for(int i = 0; i < s.length(); i++){
            char c = s.charAt(i);
            if(c == '(' || c == '[' || c == '{'){
                stack[++index] = c;
            }else{
                if(index == -1){
                    return false;
                }
                if((c == ')' && stack[index] == '(') || (c == ']' && stack[index] == '[') || (c == '}' && stack[index] == '{')){
                    index--;
                }else{
                    return false;
                }
            }
        }

        return index == -1;
    }
}

636. 函数的独占时间 - 力扣（LeetCode）

 

这个题目好长，单线程中第i个函数的独占时间，他告诉我每个函数的开始和结束时间，要我用数组的形式返回。 

通过维护一个栈来跟踪函数调用，根据日志中的信息更新每个函数的执行时长。注释中详细解释了各个部分的功能。

 

class Solution {
    public int[] exclusiveTime(int n, List logs) {
        // 用于存储每个函数执行的总时长
        int[] durations = new int[n];
        
        // 使用栈来追踪函数调用
        Stack stack = new Stack<>();
        
        // 遍历日志列表
        for (String log : logs) {
            // 解析日志中的函数编号、是否为开始、以及时间戳
            int func = func(log);
            boolean isStart = isStart(log);
            int time = time(log);
            
            if (isStart) {
                // 如果是函数调用的开始，将开始时间和间隔（初始为0）入栈
                stack.push(new int[]{time, 0});
            } else {
                // 如果是函数调用的结束，弹出栈顶元素，并计算该函数执行的时长
                int[] start = stack.pop();
                int startTime = start[0];
                int gap = start[1];
                int duration = time - startTime + 1 - gap;
                durations[func] += duration;
                
                // 如果栈不为空，更新栈顶元素的间隔
                if (!stack.empty()) {
                    gap += duration;
                    stack.peek()[1] += gap;
                }
            }
        }
        
        // 返回每个函数执行的总时长数组
        return durations;
    }

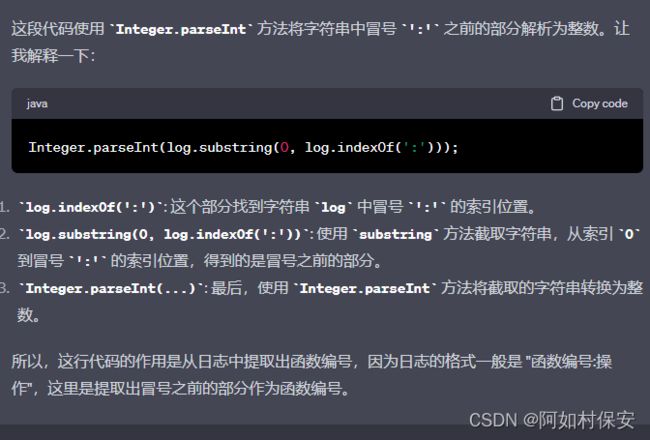
    // 解析日志中的函数编号
    private int func(String log) {
        return Integer.parseInt(log.substring(0, log.indexOf(':')));
    }

    // 判断日志是否为函数调用的开始
    private boolean isStart(String log) {
        return log.contains("start");
    }

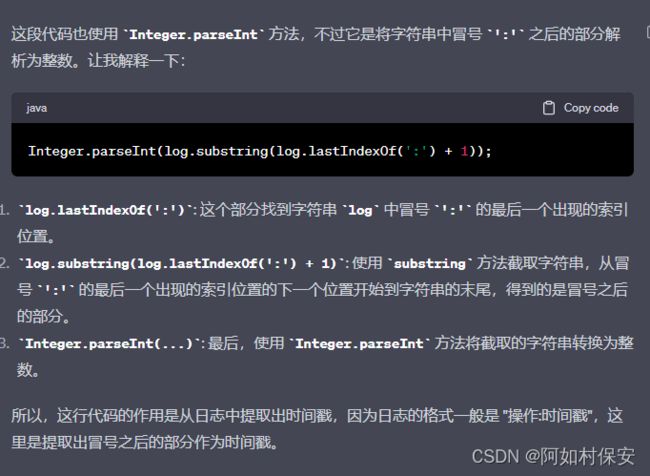
    // 解析日志中的时间戳
    private int time(String log) {
        return Integer.parseInt(log.substring(log.lastIndexOf(':') + 1));
    }
}

591. 标签验证器 - 力扣（LeetCode）

讲实话，这个还不太想看，之后看吧 

class Solution {
    public boolean isValid(String code) {
        boolean bottom = false;
        Deque stack = new ArrayDeque<>();
        try {
            for (int i = 0; i < code.length(); ) {
                if (code.charAt(i) == '<') {
                    if (code.charAt(i + 1) == '/') {
                        String cmp = String.valueOf(stack.peek());
                        if (cmp.equals(code.substring(i, i + cmp.length()))) {
                            stack.poll();
                            i += cmp.length();
                        } else return false;
                    }
                    else if (code.charAt(i+1)!='!'){  //标签开头判断部分
                        i++;
                        boolean judge = false;
                        StringBuilder str = new StringBuilder("') return false;
                        for (int j = 0; j <= 9; j++) {
                            if (!(code.charAt(i + j) >= 65 && code.charAt(i + j) <= 90) && code.charAt(i + j) != '>')
                                return false;
                            else if (code.charAt(i + j) == '>') {
                                str.append('>');
                                stack.push(str);
                                judge = true;
                                i += j;
                                break;
                            } else str.append(code.charAt(i + j));
                        }
                        if (!judge) return false;
                    }
                    //CDATA判断部分
                    else if (code.substring(i, i + 9).equals("")) {
                            i++;
                        }
                        if (code.substring(i, i + 3).equals("]]>")) i += 3;
                    }else return false;
                } else if (!stack.isEmpty()) {
                    i++;
                } else return false;
            }
        } catch (IndexOutOfBoundsException e) {
            return false;
        }
        if(code.equals("")) return false;
        return stack.isEmpty();
    }
}

32. 最长有效括号 - 力扣（LeetCode）

 找出给定字符串中最长的有效括号子串的长度。通过维护数组 pb 来记录以每个字符结尾的可能的最长有效括号长度，并在遍历过程中更新最大长度。

这个题Mark一下，我想用之前的一个思路（20. 有效的括号 - 力扣（LeetCode））做一下，但我感觉有点不对，有种情况没考虑，之后做一下

class Solution {
    public int longestValidParentheses(String s) {
        int max = 0; // 用于记录最长有效括号的长度
        char[] chs = s.toCharArray(); // 将输入字符串转换为字符数组
        int[] pb = new int[chs.length]; // 用于存储以每个字符结尾的最长有效括号长度

        for (int i = 1; i < chs.length; i++) {
            if (chs[i] == '(') {
                continue; // 如果当前字符是'('，则跳过，因为以'('结尾的子串不可能是有效括号
            }

            // 计算以当前字符结尾的可能的最长有效括号长度
            int j = pb[i-1] == 0 ? i - 1 : i - 1 - pb[i-1];

            // 如果 j 合法且对应的字符是'('，则更新 pb[i]
            if (j >= 0 && chs[j] == '(') {
                pb[i] = i - j + 1;

                // 如果前面还有有效括号，累加长度
                if (i - pb[i] >= 0 && pb[i - pb[i]] > 0) {
                    pb[i] += pb[i - pb[i]];
                }

                // 更新最大长度
                max = Math.max(max, pb[i]);
            }
        }

        return max; // 返回最长有效括号的长度
    }
}

 

---

总结

其实这个地方，很多用到了栈的思想，但没有用栈，这三部分的题感觉之后还要好好复习一下，还有面向对象的编程也要加强一下，多敲。