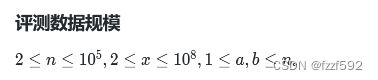蓝桥杯第三场双周赛（AK）

题目非常典型，很适合学算法。

1111 第 3 场算法双周赛 - 蓝桥云课

双十一的祈祷

        题意：求的个位数。

        思路：只需要求个位数，因此此题等效于求 ,可用快速幂或者直接看出为1。

#include 
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N=1e05+10;
const LL mod = 10;
typedef pairpl;
priority_queue, greater >t;
priority_queue q;
LL gcd(LL a, LL b){
	return b > 0 ? gcd(b , a % b) : a;
}

LL lcm(LL a , LL b){
	return a / gcd(a , b) * b;
}
LL qpow(LL a , LL b)//快速幂
{
	LL sum=1;
	while(b){
		if(b&1){
			sum=sum*a%mod;
		}
		a=a*a%mod;
		b>>=1;
	}
	return sum;
}
void solve() 
{
	cout<>t;
    while(t--)
    {
    	solve();
    }
    return 0;
}

疯狂的促销

        题意：三个电商平台优惠不同，现有若干商品，每个商品可以任选平台，求购买所有商品的最低价格。

        思路：直接模拟。

        

#include 
using namespace std;
int algo(int cost){
  int cost1 , cost2 , cost3;
  cost1 = cost >= 500 ? cost - cost / 10 : cost;
  cost2 = cost >= 1000 ? cost - 150 : cost;
  cost3 = cost == 1111 ? 0 : cost - cost / 20;
  return min(cost1 , min(cost2 , cost3));
}
int main()
{
  // 请在此输入您的代码
  int n;
  cin>>n;
  long long sum = 0;
  for(int i = 0 ; i < n ; i ++){
    int num;
    cin>>num;
    sum += algo(num);
  }
  cout<

被替换的身份证

        题意：两个人有两张牌，根据规则谁先出完牌谁赢。

        思路：还是模拟，考虑先手获胜情况：1、有对子/王炸。2、自己最大的牌比对面能打的最大的牌要大。其余都是后手赢。

        

#include 
#include 
using namespace std;
int main()
{
  // 请在此输入您的代码
  int n;
  cin>>n;
  mapmp;
  string mask = "3456789XJQKA2MF";
  for(int i = 0 ; i < mask.size() ; i ++){
    mp[mask[i]] = i;
  }
  while(n--){
    string s1 , s2;
    cin >> s1 >> s2;
    int sd_1 , sd_2 , j_1 , j_2;
    sd_1 = mp[s1[0]];
    sd_2 = mp[s1[1]];
    j_1 = mp[s2[0]];
    j_2 = mp[s2[1]];
    if(sd_1 > sd_2){
      swap(sd_1 , sd_2);
    }
    if(j_1 > j_2){
      swap(j_1,j_2);
    }
    if(sd_1 == 13 && sd_2 == 14){
      cout<<"ShallowDream";
    }
    else if(sd_1 == sd_2){
      cout<<"ShallowDream";      
    }
    else if(j_1 == 13 && j_2 == 14){
      cout<<"Joker";
    }
    else if(sd_2 >= j_2){
      cout<<"ShallowDream";
    }
    else{
      cout<<"Joker";
    }
    cout<

迷宫逃脱

        题意：迷宫问题，从左上角走到右下角，只能往右或者往下走，每个格子中含有一个数字，若从 走到 的两个格子中的数字互质，则需要一把钥匙才能走。现在共有 k 把钥匙。求从左上角走到右下角的路径上数字之和的最大值。

        思路：观察到迷宫格子数（1e6）, 钥匙数（3）因此考虑 来做。定义为走到第行的第列，消耗了把钥匙的路径之和最大值。状态转移方程：(互质情况）

（非互质情况）

#include 
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N=1e05+10;
const LL mod=1e09+7;
typedef pairpl;
priority_queue, greater >t;
priority_queue q;
LL gcd(LL a, LL b){
	return b > 0 ? gcd(b , a % b) : a;
}

LL lcm(LL a , LL b){
	return a / gcd(a , b) * b;
}         
int main() 
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cout.precision(10);
	int  n , m  , q;
	cin >> n >> m >> q;
	LL a[n + 5][m + 5];
	LL dp[n + 5][m + 5][q + 5];
	memset(dp , -0x3f3f, sizeof dp);
	for(int i = 1; i <= n ; i ++)
		for(int j = 1 ; j <= m ; j ++)
			cin >> a[i][j];
	dp[1][1][0] = a[1][1];
	for(int i = 1 ; i <= n ; i ++){
		for(int j = 1 ; j <= m ; j ++){
			for(int k = 0 ; k <= q; k ++){
				//从上方转移
				if(i > 1){
					if(gcd(a[i - 1][j] , a[i][j]) == 1){
						if(k > 0){
							dp[i][j][k] = max(dp[i][j][k] , dp[i - 1][j][k - 1] + a[i][j]);
						}
					}
					else{
						dp[i][j][k] = max(dp[i][j][k] , dp[i - 1][j][k] + a[i][j]);
					}
				}
				//从左侧转移
				if(j > 1){
					if(gcd(a[i][j - 1] , a[i][j]) == 1){
						if(k > 0){
							dp[i][j][k] = max(dp[i][j][k] , dp[i][j - 1][k - 1] + a[i][j]);
						}
					}
					else{
							dp[i][j][k] = max(dp[i][j][k] , dp[i][j - 1][k] + a[i][j]);						
					}
				}
			}
		}
	}
	LL maxx = -1e18;
	for(int i = 0 ; i <= q; i ++){
		maxx = max(maxx , dp[n][m][i]);
	}
	if(maxx > 0)
		cout<

深秋的苹果

        题意：给定一个数组，要求分成m段连续子序列，定义一段子序列的价值为，求分成m段连续子序列中子序列价值的最大值的最小值。

        思路：最值问题考虑二分来解答，二分子序列价值的最大值即可。

#include 
using namespace std;
const int N = 2e5 + 10;
int n , m;
int a[N];
bool check(long long c){
  long long cnt = 1;
  long long sum = 0;
  long long tt = 0;
  for(int i = 0 ; i < n ; i ++){
      if(tt + sum * a[i] > c){
        cnt ++;
        tt = 0;
        sum = a[i];
      }
      else{
        tt += sum * a[i];
        sum += a[i];
      }
  }
  if(cnt <= m){
    return true;
  }
  else{
    return false;
  }
}
int main()
{
  // 请在此输入您的代码
  cin >> n >> m;
  for(int i = 0 ; i < n ; i ++)
    cin>>a[i];
  long long l = 0 , r = 3e18;
  while(l < r){
    long long mid = (l + r) / 2;
    if(check(mid)){
      r = mid;
    }
    else{
      l = mid + 1;
    }
  }
  cout<

 鲜花之海

在一个幻想的王国中，有一个美丽的花园，花园里开满了各种不同颜色的鲜花。现在花园里一共有  朵鲜花，这些鲜花都有一个独特且 唯一 的编号，编号由 两个数字组成。

这些鲜花按如下规则摆放在花坛中（花坛可以视作一条直线）：

1. 如果第  朵鲜花的编号之和 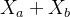小于第  朵鲜花编号之和 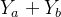，则 XX 朵鲜花放在 YY 朵鲜花前面。
2. 如果第 朵鲜花的编号之和 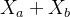等于第 朵鲜花编号之和 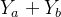，则哪一朵鲜花的编号 更小，哪一朵鲜花就摆在前面。

现在小蓝需要找到花园中的第 朵鲜花，但鲜花实在是太多了，他不想一朵朵的去找，你可以快速的告诉他第  朵鲜花的编号吗。

        思路：参考曼哈顿距离，将原正方形顺时针旋转90°之后再镜像一下得到一个菱形，其中第一行只有一个元素 , 第二行有两个元素....共有行，且上面一行的两坐标之和必然小于下面一行。由于N很大，因此无法通过遍历N来找出第朵花。对于整个菱形而言，前x行的总数是能够快速得到的，因此考虑二分第朵花所在的行，然后再快速求出其坐标。

        

#include 
using namespace std;
long long n , k;
long long cnt(long long r){
  long long res = 0;
  if(r > n){
    res += (n + 1) * n / 2;
    res += (n - 1 + (n - (r - n))) * (r - n) / 2; 
  }
  else{
    res += (1 + r) * r / 2;
  }	
  return res;
}
bool check(long long r){
  long long res = cnt(r);
  if(res >= k){
    return true;
  }
  else{
    return false;
  }
}
int main()
{
  // 请在此输入您的代
  int t;
  cin >> t;
  while(t--){
	  cin >> n >> k;
	  long long l = 0 , r = 2 * n - 1;
	  while(l < r){
	    long long mid = (l + r) / 2;
	    if(check(mid)){
	      r = mid;
	    }
	    else{
	      l = mid + 1;
	    }
	  }
	  k -= cnt(l - 1);
	  if(l <= n){
	  	int sum = l + 1;
	  	int x = k;
	  	int y = sum - k;
	  	cout << x << " " << y << endl;
	  }
	  else{
	  	int sum = l + 1;
	  	int x = k + (r - n);
	  	int y = sum - x;
	  	cout << x << " " << y << endl;
	  }
  }
  return 0;
}

斐波拉契跳跃

        题意：博弈游戏，小蓝和小桥在玩一个数学游戏，游戏规则如下：有一个长度为  的 排列   和一个棋子，两个人轮流按照游戏规则在排列上移动这个棋子，由小蓝先手，最先不能移动棋子的人判为输。对于某一次移动，设棋子的移动起点为 ，移动的终点为 ，两人移动棋子均需要满足以下游戏规则：

        1、。

        2、是一个斐波那契数。且跳跃的距离要严格大于上一次所跳跃的距离。

        思路：建立函数，定义为第个点，上一步已经跳了第个斐波那契数的距离之后是否能走出最后一步，若移动之后无法再移动了，则 = 1（代表了必胜）, 反之（代表必输）.。其中表示自身状态，若 , 则该点必输。由于每个点所能跳跃的点十分有限，因此考虑dfs+记忆化搜索来遍历所有可能情况。

        

#include 
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N=1e05+10;
const LL mod=1e09+7;
typedef pairpl;
priority_queue, greater >t;
priority_queue q;
LL gcd(LL a, LL b){
    return b > 0 ? gcd(b , a % b) : a;
}
LL lcm(LL a , LL b){
    return a / gcd(a , b) * b;
}
int n;
int fib[30];
int sg[N][30];
int a[N];
int dfs(int x , int l){
	if(sg[x][l] != -1)
		return sg[x][l];	
	int vis[2] = {0};
	for(int i = l + 1 ; i < 30 ; i ++){
		int v = fib[i];
		if(x - v >= 0 && a[x] < a[x - v]){
			dfs(x - v , i);
			vis[sg[x - v][i]] = 1;
		}
		if(x + v < n && a[x] < a[x + v]){
			dfs(x + v , i);
			vis[sg[x + v][i]] = 1;
		}
	}
	if(vis[0])
		return sg[x][l] = 1;
	else
		return sg[x][l] = 0;
}
int main() 
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cout.precision(10);
	fib[0] = 0;
	fib[1] = 1;
	fib[2] = 2;
	for(int i = 3 ; i < 30 ; i ++){
		fib[i] = fib[i - 1] + fib[i - 2];
	}
	cin>>n;
	for(int i = 0 ; i < n ; i ++){
		cin >> a[i];
	}
	memset(sg , -1 , sizeof sg);
	for(int i = 0;i < n;i++)
	{
	if(dfs(i,0) == 0)
		cout<<"Little Qiao"<

星石传送阵

       

        思路：首先答案显然是建完图之后BFS。对于求,需要求出所有的质因子之和（由于要求价值之和最小，假设有一个能量为x * x的星石，那么将其拆为x + x 两块星石的总价值会更小）。需要先把1 ~ 1e4上所有的素数都找出来。然后再对 x 分解质因子。 接下来考虑如何去建图，对于规则2而言，编号为 和编号为的相连，那么总共只会有最多条边（每个编号一条边）。但是对于规则1而言，若每个能量阵的都相同，那么需要建条边，这是无法接受的。因此不能用操作1来建边。因为其边权值都为1，那么无需存边，只需要将相等的点放一起即可。在BFS的过程中，对于能量值为 x 的传送阵而言，下一步只需要将相等的所有的点全部放进去即可，然后又因为此次操作做完以后所有的点全都放进去了，下次再碰到时无需再遍历相等的所有的点，如此便能无需建边且不重复的BFS。

        

#include 
using namespace std;
#define LL long long
#define pb push_back
#define x first
#define y second 
#define endl '\n'
const LL maxn = 4e05+7;
const LL N = 2e05+10;
const LL NN = 1e4;
const LL mod=1e09+7;
typedef pairpl;
priority_queue, greater >t;
priority_queue q;
LL gcd(LL a, LL b){
	return b > 0 ? gcd(b , a % b) : a;
}
LL lcm(LL a , LL b){
	return a / gcd(a , b) * b;
}
vectorprime;//存储素数
bool vis[N+5];
vectormp[N];
int depth[N];
int vi[N];//x是否进去
int v[N];//f[i]是否进去
int n , A , B;
struct Node{
	int x;
	int fx;
}a[N];
vectorf[N];
void su() 
{
	for(int i = 2;i <= NN;i++)
	{
		if(!vis[i])
		  prime.pb(i);
		for(int j=0;j < prime.size() && prime[j] * i <= NN;j ++)
		{
			vis[prime[j]*i]=1;
			if(i % prime[j]==0)
			break;
		}
	}
}  
int fun(int a){
	int len = prime.size();
	int sum = 0;
	for(int i = 0 ; i < len ; i++){
		int x = prime[i];
		if(a < x){
			break;
		}
		while(a % x == 0){
			sum += x;
			a /= x;
		}
	}
	if(a > 1){
		sum += a;
	}
	return (sum % n) + 1;
}
void dfs(){
	queueq;
	q.push(A);
	vi[A] = 1;
	depth[A] = 0;
	while(!q.empty()){
		int x = q.front();
		q.pop();
		for(auto it : mp[x]){
			if(!vi[it]){
				depth[it] = depth[x] + 1;
				q.push(it);
				vi[it] = 1;
			}
		}
		int F = a[x].fx;
		if(v[F] == 0){
			for(auto it : f[F]){
				if(!vi[it]){
					depth[it] = depth[x] + 1;
					q.push(it);
					vi[it] = 1;
				}				
			}
			v[F] = 1;
		}
	}
}
int main() 
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cout.precision(10);
	su();
	cin >> n >> A >> B;
	for(int i = 0 ; i <= n ; i ++){
		depth[i] = -1;
	}
	for(int i = 1 ; i <= n ; i ++){
		cin >> a[i].x;
		a[i].fx = fun(a[i].x);
		mp[i].pb(a[i].fx);
		mp[a[i].fx].pb(i);
		f[a[i].fx].pb(i);
	}
	dfs();
	cout<