常见的求最大公约数的方法
最大公约数
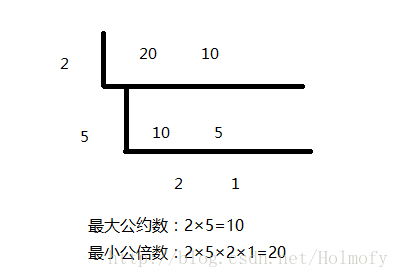
最大公约数和最小公倍数求解,常用的方法是短除法进行因式分解,然后最大公约数是所有公共因子的乘积,最小公倍数是所有因子的乘积。
本质上求最小公倍数就是求最大公倍数:x=m*a, y=m*b;m是最大公约数,那最小公倍数就是m*a*b。所以可以得到最大公约数与最小公倍数的关系:
LCM(A,B)×GCD(A,B)=A×BLCM(A,B)×GCD(A,B)=A×B
其中LCM是最小公倍数,GCD是最大公约数
用代码来表示就是:
// LCM:least common multiple
// GCD:greatest common divisor
int LCM(int a, int b) {
int gcd = GCD(a, b);
return a * b / gcd;
}123456
所以重点就是求最大公约数。
常见的求最大公约数的方法有
- 分解因式法
- 辗转相除法
- 更相减损法
- Stein算法
扩展欧几里得算法是后加进来的,它解决的不单纯是求最大公约数的问题,本不应该放进来。因为本文介绍了欧几里得算法,权衡利弊后也就顺带把扩展欧几里得算法讲一下。
公约数的性质
在介绍算法之前,我们需要先了解一下公约数的几个重要性质,这几个性质在后面几个算法中会用到(用到时再证明,以免数学不感冒的人看的头痛):
如果b是A和B的公约数,那么:
- b也是A+B的约数,即b是A,B,A+B的公约数
- b也是A-B的约数,即b是A,B,A-B的公约数
- 更一般地,对于任意整数x、y,b也是Ax+By的约数,即b是A,B,Ax+By的公约数
- 根据上一条性质,r = A - kB = A mod B,所以A mod B也是A+B的约数,mod是求余运算,即b是A,B,A mod B的公约数
用式子写出来即:
gcd(A,B) = gcd(B,A) = gcd(A,A+B) = gcd(A,A-B) = gcd(A,Ax+By) = gcd(A,A mod B)
1.分解因式法
很显然因式分解不是一个好方法,看下面实现代码就知道很耗性能,而且还不能对0处理。
// greatest common divisor
int GCD(int a, int b) {
assert(a != 0);
assert(b != 0);
int min = a < b ? a : b;
int accumulate = 1;
// 以2进行分解,如果0进来这里就死循环了
while ((a & 1) == 0 && (b & 1) == 0) {
accumulate *= 2;
a >>= 1;
b >>= 1;
}
// 以大于等于3的数进行分解
for (int i = 3; i <= min; i += 2) {
while ((a % i) == 0 && (b % i) == 0) {
accumulate *= i;
a /= i;
b /= i;
}
}
// 将所有公因子的乘积作为返回值
return accumulate;
}
虽然暴力法代码冗长,性能低下,但对于后面的几个算法仍具有参考意义。
2.更相减损术
定义:
更相减损法原本是为了约分而设计的:可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也。以等数约之。
1:任意给定两个正整数;判断它们是否都是偶数。若是,则用2约简;若不是则执行第二步。
2:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数。继续这个操作,直到所得的减数和差相等为止。
第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数,相当于不要第一步。
换成公式的写法:
如果A > B,则 gcd(A,B) = gcd(B,A-B)
如果A < B,则 gcd(A,B) = gcd(A,B-A)12
下面这张图是维基百科中对欧几里得算法的描述,但实际上这张图并没有直接求余数,而是两者相减,和更相减损法如出一辙。
证明:
不妨设A>B,设A和B的最大公约数为X,所以 A=aX,B=bx,其中a和b都为正整数,切a>b。
C = A-B,则有:
>C=aX−bX=(a−b)X>>C=aX−bX=(a−b)X>
因为a和b均为正整数,所以C也能被X整除,即A、B、C最大公约数均为X
所以
gcd(A,B) = gcd(B,A-B)
代码
int GCD(int a, int b) {
while (a != b) {
if (a > b)
a = a - b;
else
b = b - a;
}
return a;
}
3.辗转相除法
辗转相除法(中国叫法)也叫欧几里得算法(国外叫法)。
该算法定义如下:两个正整数A,B的最大公约数等于其中较小值与两数相除的余数的最大公约数。
写成公式就是:
gcd(A, B) = gcd(B, A mod B) 其中:A > B1
证明
不妨设A > B,设A和B的最大公约数为X,所以 A=aX,B=bX,其中a和b都为正整数且a>b。
A除以B的余数:
R = A - k*B,其中k为正整数是A除以B的商,所以:>R=A−k∗B=aX−kbX=(a−kb)X>>R=A−k∗B=aX−kbX=(a−kb)X>
因为a、k、b均为正整数,所以R也能被X整除
即A、B、R的公约数相同,所以有gcd(A,B) = gcd(B,A mod B)
最小公倍数可通过先求最大公因数再引用公式的方法。
最小公倍数可以通过多种方法得到,最直接的方法是列举法,从小到大列举出其中一个数(如最大数)的倍数,当这个倍数也是另一个数的倍数时,就求得最小公倍数。另一个方法是利用公式[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ftrfVvLr-1622980225052)(https://wikimedia.org/api/rest_v1/media/math/render/svg/0b311081f8e412bdcb66d43a9d36c1f60aec031b)]来求解,这时首先要知道它们的最大公因数。而最大公因数可以通过短除法得到。
//递归
int GCD(int a, int b)
{
return b == 0 ? a : GCD(b, a%b);
}
//将递归化成循环
int gcd(int m,int n)
{
while(m % n != 0)
{
int r = m % n;
m = n;
n = r;
}
return n;
}
4.测试
/**< 测试几种求最大公约数的算法 */
#include 5.辗转相除法与更相减损术的比较
(1)两者都是求最大公因数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到。
6.Stein算法
欧几里德算法是计算两个数最大公约数的传统算法,无论从理论还是从实际效率上都是很好的。但是却有一个致命的缺陷,这个缺陷在素数比较小的时候一般是感觉不到的,只有在大素数时才会显现出来:一般实际应用中的整数很少会超过64位(当然现在已经允许128位了),对于这样的整数,计算两个数之间的模是很简单的。对于字长为32位的平台,计算两个不超过32位的整数的模,只需要一个指令周期,而计算64位以下的整数模,也不过几个周期而已。但是对于更大的素数,这样的计算过程就不得不由用户来设计,为了计算两个超过64位的整数的模,用户也许不得不采用类似于多位数除法手算过程中的试商法,这个过程不但复杂,而且消耗了很多CPU时间。对于现代密码算法,要求计算128位以上的素数的情况比比皆是,比如说RSA加密算法至少要求500bit密钥长度,设计这样的程序迫切希望能够抛弃除法和取模。
Stein算法很好的解决了欧几里德算法中的这个缺陷,Stein算法只有整数的移位和加减法。下面就来说一下Stein算法的原理:
- 若a和b都是偶数,则记录下公约数2,然后都除2(即右移1位);
- 若其中一个数是偶数,则偶数除2,因为此时2不可能是这两个数的公约数了
- 若两个都是奇数,则a = |a-b|,b = min(a,b),因为若d是a和b的公约数,那么d也是|a-b|和min(a,b)的公约数。
这里面可能就第三句话难理解一点,这里进行简单的证明:
不妨设奇数A>B,A和B的公约数为X,即A=jX,B=kX,其中j,k均为正整数且j>k。
>A−B=(j−k)X>>A−B=(j−k)X>
因为j,k均为整数,所以X也是A-B的公约数。
min(A,B)=B
所以A-B与min(A,B)公约数相同,因为A,B都是奇数,所以A-B必然是偶数,偶数又可以二除移位了。
代码实现:
下面代码中以int作为参数,
int SteinGCD(int a, int b) {
if (a < b) { int t = a; a = b; b = t; }
if (b == 0) return a;
if ((a & 1) == 0 && (b & 1) == 0)
return SteinGCD(a >> 1, b >> 1) << 1;
else if ((a & 1) == 0 && (b & 1) != 0)
return SteinGCD(a >> 1, b);
else if ((a & 1) != 0 && (b & 1) == 0)
return SteinGCD(a, b >> 1);
else
return SteinGCD(a - b, b);
}123456789101112
将递归化成循环
int SteinGCD(int a, int b) {
int acc = 0;
while ((a & 1) == 0 && (b & 1) == 0) {
acc++;
a >>= 1;
b >>= 1;
}
while ((a & 1) == 0) a >>= 1;
while ((b & 1) == 0) b >>= 1;
if (a < b) { int t = a; a = b; b = t; }
while ((a = (a - b) >> 1) != 0) {
while ((a & 1) == 0) a >>= 1;
if (a < b) { int t = a; a = b; b = t; }
}
return b << acc;
}