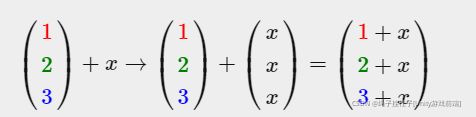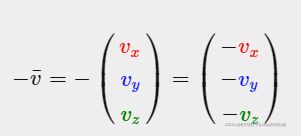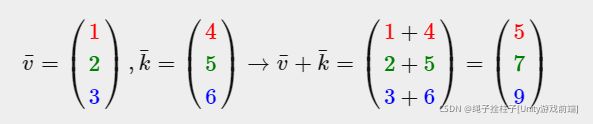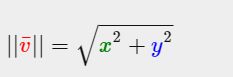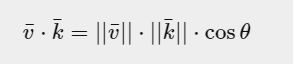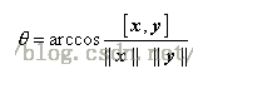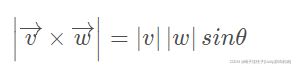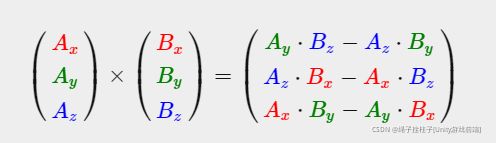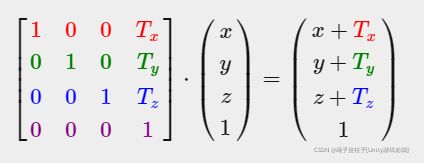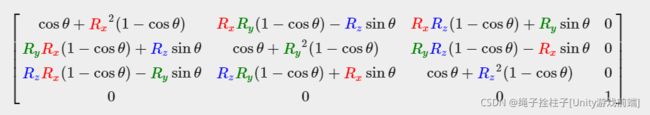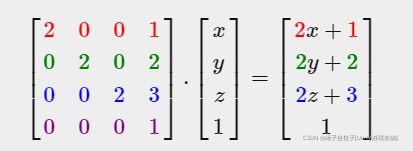Learn OpenGL 笔记2.7 - Transformations
基础知识:
1.Vectors
在最基本的定义中,向量是方向。向量具有方向和大小(也称为强度或长度)。
2.Scalar vector operations (标量向量运算)
3.Vector negation(负)
4.Addition and subtraction(加减)
5.normalizing (标准化)
就是本身v,除以三角形第三条边的长度
6.Vector-vector multiplication (积)
Dot product (点积)
向量的点积,也叫向量的内积、数量积,对两个向量执行点乘运算,就是对这两个向量对应位置一一相乘之后求和的操作,点乘的结果是一个标量
3.比较两个向量的接近程度(方向上)
也就是向量是否两个向量间的夹角大小,在聚光灯的效果计算中,可以根据点积来得到光照效果,如果点积越大,说明夹角越小,则物体离光照的轴线越近,光照越强。
也常会用来判断两向量是否为同方向:
a·b>0 方向基本相同,夹角在0°到90°之间
a·b=0 正交,相互垂直
a·b<0 方向基本相反,夹角在90°到180°之间
Cross product(叉积)
向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。
几何意义:
在二维空间,两个向量叉积就是两向量形成的平行四边形的面积,正负要引入Z轴,由右手螺旋定则确定,如果大拇指指向Z正轴就为正,反之为负;
在三维空间,两个向量叉积就是垂直于两向量形成的平面的向量(称为法向量)采用右手螺旋定则确定方向。v到w的方向就是右手四指弯曲的方向,大拇指的方向就是叉积的方向。
右手螺旋确定方向:
![]()
这位大佬的文章,建议全文背诵
点积和叉积在计算机图形学的应用_from_the_star的博客-CSDN博客_叉乘应用
7.Matrices
矩阵是由数字、符号和/或数学表达式组成的矩形阵列。 矩阵中的每一项都称为矩阵的一个元素。
1.Addition and subtraction(加减)
2.Matrix-scalar products(标量乘)
3.Matrix-matrix multiplication(矩阵乘)
8.Matrix-Vector multiplication
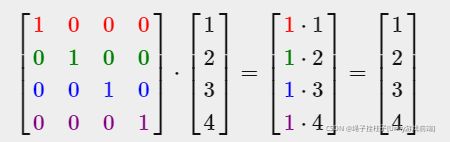
1.Identity matrix(单位矩阵)
2.Scaling(缩放)
3.Translation(平移变换)
4.Homogeneous coordinates(齐次坐标)
矢量的 w 分量(x,y,z,w)也称为齐次坐标。 为了从齐次向量中获得 3D 向量,我们将 x、y 和 z 坐标除以其 w 坐标。 我们通常不会注意到这一点,因为 w 分量大部分时间都是 1.0。 使用齐次坐标有几个优点:它允许我们对 3D 向量进行矩阵转换(Tx,Ty,Tz都需要w分量).
当齐次坐标等于 0 时,该向量特别称为方向向量,因为 w 坐标为 0 的向量无法平移。
齐次坐标就是用N+1维来代表N维坐标
我们把齐次坐标转化为笛卡尔坐标的方法是前面n-1个坐标分量分别除以最后一个分量即可
使用齐次坐标,可以表示 平行线在透视空间的无穷远处交于一点。在欧氏空间,这变得没有意义,所以欧式坐标不能表示。
即:齐次坐标可以表示无穷远处的点
如果点(1,2)移动到无限远处,在笛卡尔坐标下它变为(∞,∞),然后它的齐次坐标表示为(1,2,0),因为(1/0, 2/0) =
(∞,∞),我们可以不用”∞"来表示一个无穷远处的点了。
这位大佬的文章,建议全文背诵
为什么要引入齐次坐标,齐次坐标的意义(一)_追求卓越583的博客-CSDN博客_齐次坐标
5.Rotation(旋转)
6.Combining matrices(组合矩阵)
2.实践代码:
旋转箱子
vetex shader 代码:
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;
out vec2 TexCoord;
uniform mat4 transform;
void main()
{
gl_Position = transform * vec4(aPos, 1.0f);
TexCoord = vec2(aTexCoord.x, aTexCoord.y);
} 2.1 gl_Position(这个真的难懂,明天实践操作一波,11/11已经搞定)
自己总结:
aPos表示vetex Shader顶点着色器传过来的3维顶点坐标,gl_Position表示归一化的坐标,之前的笔记有解释,由vec3加上一个参数变成vec4的原因,可以利用第四个参数,精准表示无穷大远处的坐标。也就是笛卡尔坐标转化为齐次坐标。
网上的说法:
其中 gl_Position,默认是归一化(xyz各个维度的范围为-1到1)的裁剪空间坐标
仅能在顶点着色器中使用,既是输入也是输出,这个值是多少,就决定怎么裁剪空间
gl_Position赋值范围就是float的取值范围(32位),只不过只有[-1,1]区间的片元被绘制
它是vec4类型的(比3维多一维,用于齐次运算),不能重声明为dvec4等类型