A Gentle Introduction to Graph Neural Networks
A Gentle Introduction to Graph Neural Networks----《图神经网络入门》
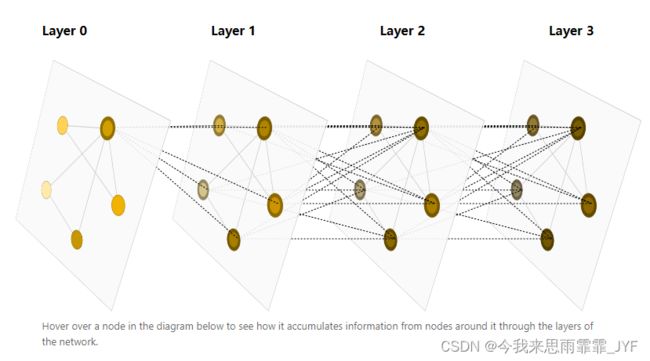
图神经网络信息传递积累
图在我们身边随处可见,现实世界中的物体通常是根据它们与其他事物的联系来定义的。一组物体以及它们之间的联系可以很自然地用图来表示。十多年来,研究人员已经开发出了可以处理图数据的神经网络,称为图神经网络或 GNN。最近的研究提高了它们的能力和表现力。我们开始看到其在多个领域的实际应用,如物理模拟、假新闻检测、交通预测和推荐系统。
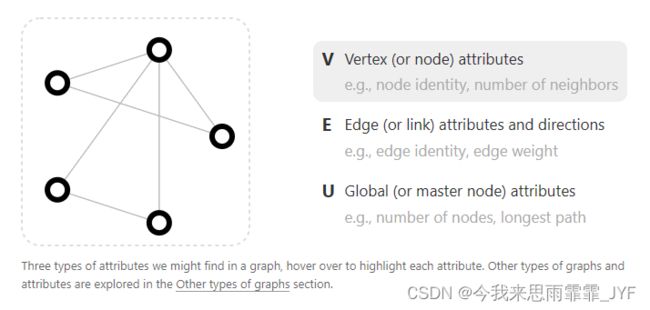
图的表示(实体(节点)集合之间的关系(边))
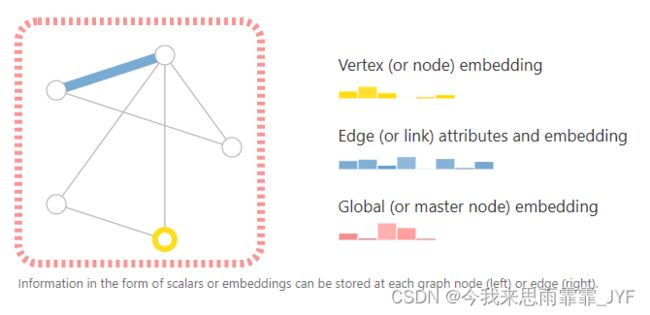
为了进一步描述每个节点、边或整个图,可以用向量表示节点、边或整个图
边的方向性(有向、无向)
图像表示成图
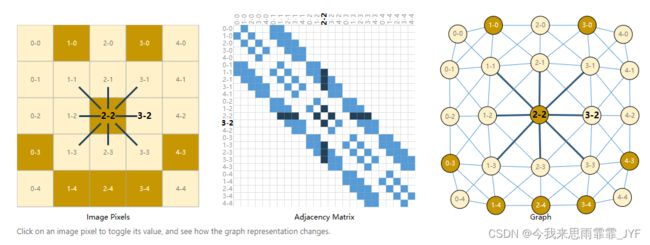
通常认为图像是带有图像通道的矩形网格,用数组(如 244x244x3 )表示。一种将图像视为具有规则结构的图的方法是,每个像素代表一个节点,并通过边与相邻像素相连。每个非边框像素正好有 8 个邻居,每个节点存储的信息是一个三维向量,代表像素的 RGB 值。
文本表示成图
为每个字符、单词或标记关联索引,并将文本表示为这些索引的序列,从而将文本数字化。这样就形成了一个简单的有向图,其中每个字符或索引都是一个节点,并通过边与后面的节点相连。
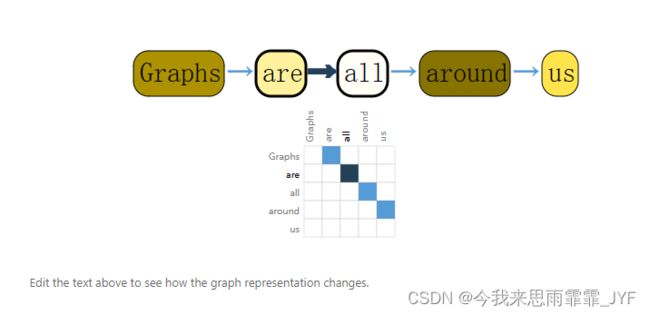
当然,在实践中,文本和图像通常不是这样编码的:这些图表示法是多余的,因为所有图像和文本都具有非常规则的结构。例如,图像的邻接矩阵具有带状结构,因为所有节点(像素)都以网格相连。文本的邻接矩阵只是一条对角线,因为每个单词只与上一个单词和下一个单词相连。
更加异构的图结构数据
社交网络表示成图。
社交网络是研究人、机构和组织集体行为模式的工具。我们可以通过将个人建模为节点,将他们之间的关系建模为边,从而建立一个代表人群的图。

与图像和文本数据不同,社交网络没有完全相同的邻接矩阵。
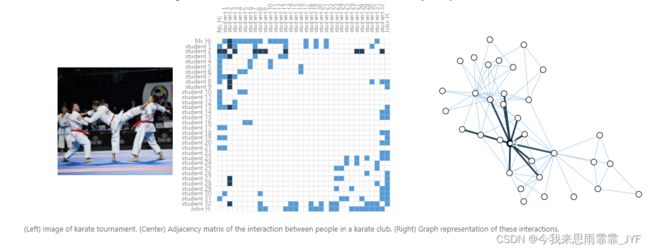
引用网络表示成图
其中每篇论文都是一个节点,每条有向边都是一篇论文与另一篇论文之间的引用。此外,我们还可以在每个节点中添加有关每篇论文的信息,如摘要。
图上的预测任务一般有三种类型:图级、节点级和边级
图级任务
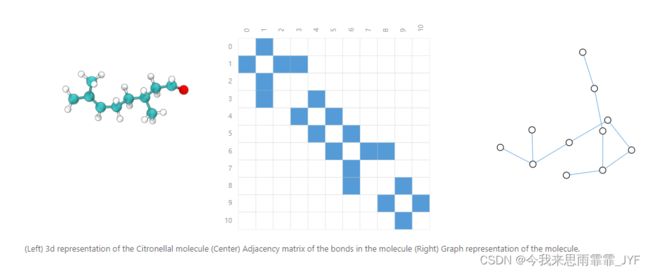
在图级任务中,目标是预测整个图的属性。例如,对于以图表示的分子,可以预测该分子的气味,或者预测它是否会与某种疾病的受体结合。
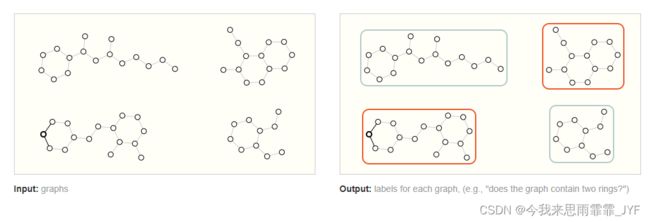
这类似于 MNIST 和 CIFAR 的图像分类问题,这里是将标签与整幅图像关联起来。对于文本,类似的问题是情感分析,即希望一次性识别整个句子的情绪或情感。
节点级任务
节点级任务涉及预测图中每个节点的身份或角色。
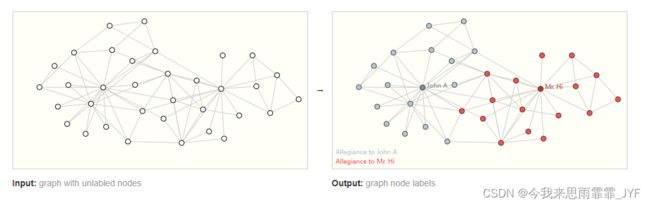
节点级预测问题的一个典型例子是扎克的空手道俱乐部。其数据集是一个单一的社交网络图,由在政治分裂后宣誓效忠于两个空手道俱乐部之一的个人组成。故事讲述的是,H 先生(教练)和 John H(管理员)之间的不和导致了空手道俱乐部的分裂。节点代表空手道练习者个人,边代表这些成员之间在空手道之外的互动。预测问题是对某个成员在不和之后是忠于 H 先生还是忠于 John H 进行分类。在这种情况下,节点与教练或管理员之间的距离与这一标签高度相关。
根据图像类比,节点级预测问题类似于图像分割,我们试图标记图像中每个像素的角色。对于文本,类似的任务是预测句子中每个单词的词性(如名词、动词、副词等)。
边级任务
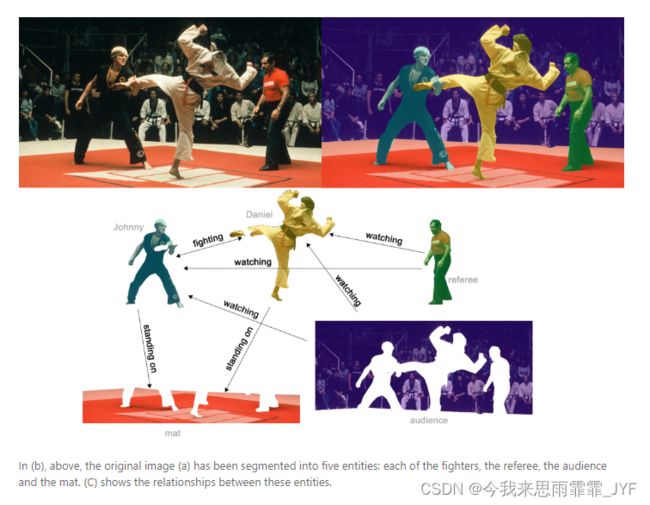
边级推理的一个例子是图像场景理解。除了识别图像中的物体,深度学习模型还可用于预测它们之间的关系。
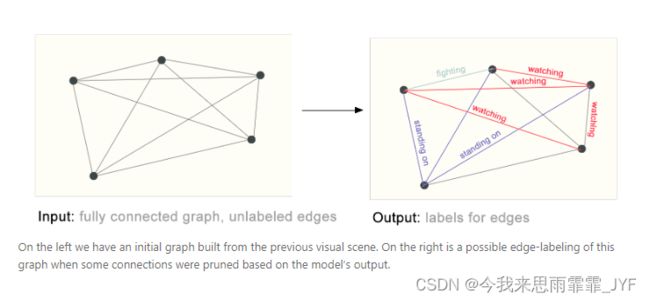
挑战
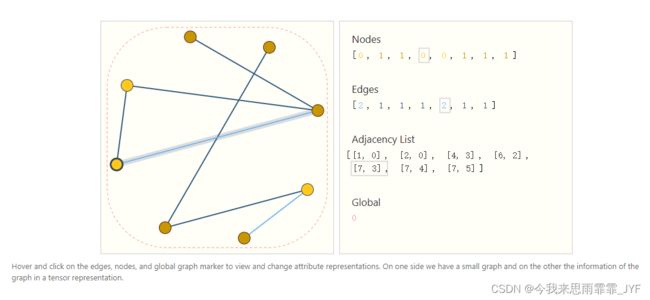
- 邻接矩阵存在稀疏性
- 邻接矩阵不唯一,不同的邻接矩阵可能会产生不同的结果
例如,前面的黑白棋图可以用这两个邻接矩阵来等价描述。它也可以用其他所有可能的节点排列来描述。

图神经网络
GNN 采用 "图入图出 "架构,即这些模型类型接受一个图作为输入,并将信息加载到其节点、边和全局上下文中,然后逐步转换这些嵌入,而不改变输入图的结构。
有了上面构建的图形数字表示法(用向量代替标量),现在就可以构建 GNN 了。我们将从最简单的 GNN 架构开始,在这个架构中,我们将学习所有图属性(节点、边、全局)的新嵌入,但我们还不会使用图的连接性。
这种 GNN 在图的每个分量上使用一个单独的多层感知器 (MLP),我们称其为 GNN 层。对于每个节点向量,我们应用 MLP,并得到一个学习到的节点向量。我们对每条边进行同样的处理,学习每条边的嵌入,同时也对全局上下文向量进行处理,学习整个图的单一嵌入。

与神经网络模块或层一样,我们可以将这些 GNN 层堆叠在一起。
由于 GNN 不会更新输入图的连接性,因此我们可以用与输入图相同的邻接表和相同数量的特征向量来描述 GNN 的输出图。但是,由于 GNN 更新了每个节点、边和全局上下文表示,因此输出图具有更新的嵌入。
通过汇集信息进行 GNN 预测
如果任务是对节点进行二元预测,而图中已经包含节点信息,那么方法就很简单–对每个节点嵌入应用线性分类器。
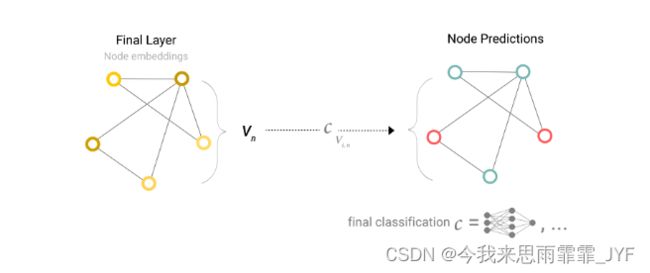
然而,事情并不总是那么简单。例如,图中的信息可能存储在边中,但节点中没有信息,但仍需要对节点进行预测。我们需要一种方法来收集边上的信息,并将其提供给节点进行预测。我们可以通过汇集来实现这一目的,将与该节点的相邻边进行求和。
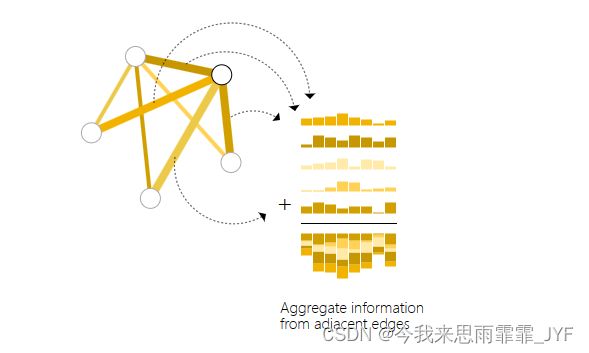
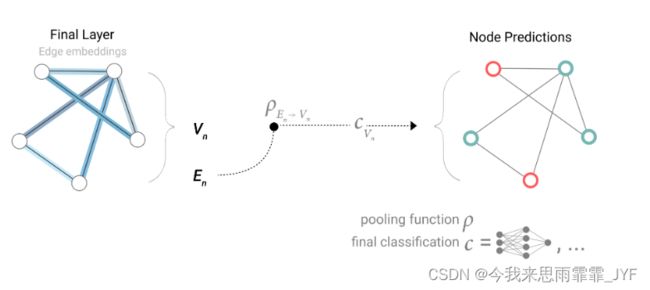
相反,如果我们只有节点级特征,并试图预测边级信息,则将这条边上的节点进行求和,那么模型看起来就像这样。
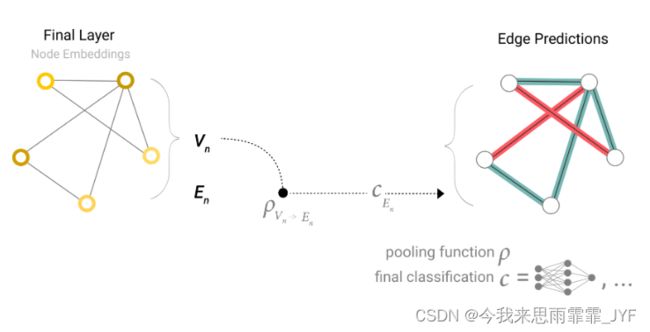
如果我们只有节点级特征,但需要预测全局属性,我们就需要将所有可用的节点信息收集在一起,然后进行聚合。这与 CNN 中的全局平均池化层类似。
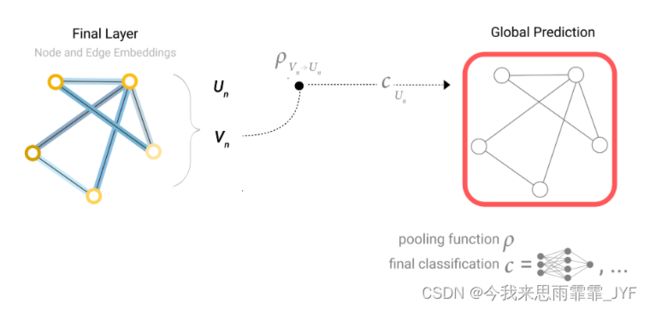
现在我们已经证明,我们可以建立一个简单的 GNN 模型,并通过在图的不同部分之间传递信息来进行二进制预测。这种汇集技术将成为构建更复杂 GNN 模型的基石。如果我们有了新的图属性,只需定义如何将信息从一个属性传递到另一个属性即可。
请注意,在这个最简单的 GNN 结构中,我们在 GNN 层内完全没有使用图的连通性。每个节点、每条边以及全局上下文都是独立处理的。我们只在汇集预测信息时使用连接性。
在图形各部分之间传递信息
我们可以使用消息传递,使相邻节点或边交换信息,并影响彼此的更新嵌入。这些步骤是利用图的连通性的关键。我们将在 GNN 层中建立更复杂的消息传递变体,从而产生表现力和功能越来越强的 GNN 模型。通过将消息传递 GNN 层堆叠在一起,一个节点最终可以整合来自整个图的信息:经过三层之后,一个节点就可以获得离它三步远的节点的信息。
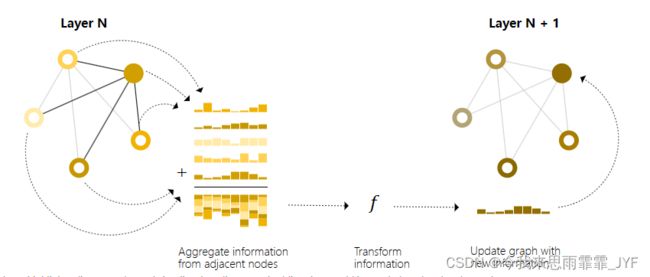
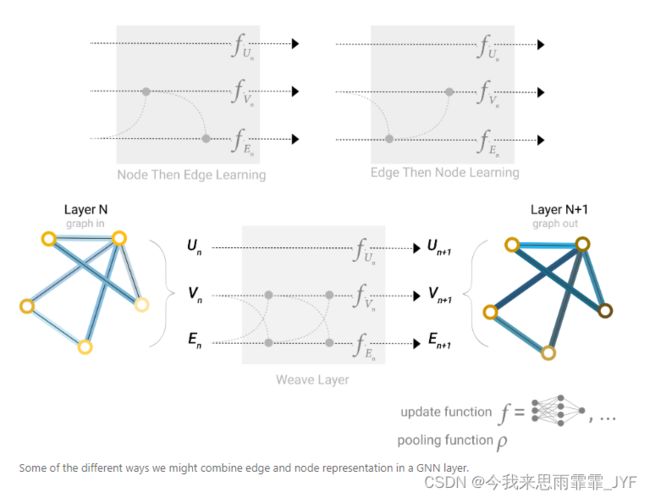
边和点传递信息的不同方式
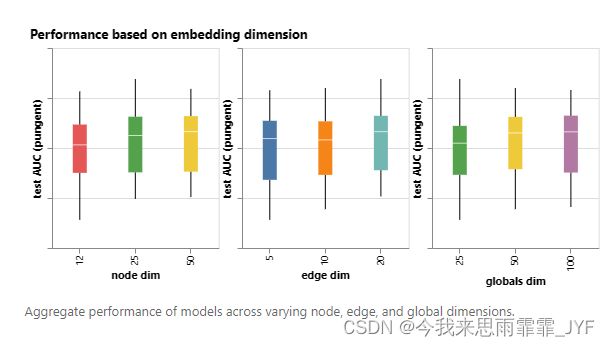
一些影响GNN性能的设计因素:信息传递方式、嵌入维度、层数和聚合操作类型。
维度越高的模型,其平均值和下限性能往往越好,但最大值却没有发现同样的趋势。
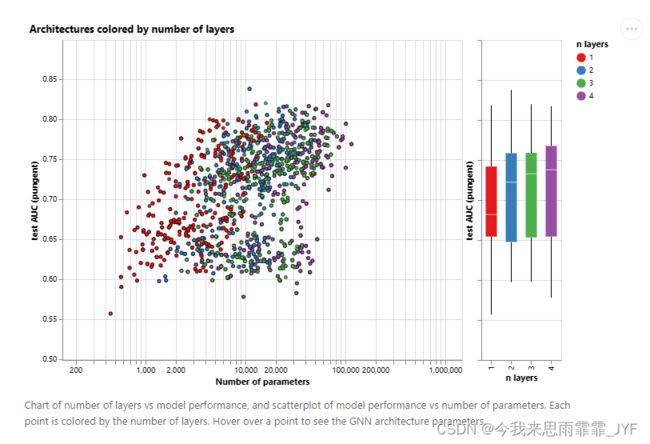
虽然平均性能随着层数的增加而增加,但性能最好的模型不是三层或四层,而是两层。此外,性能下限随着层数的增加而降低。这种效应以前也观察到过,层数越多的 GNN 传播信息的距离就越远,其节点表征就有可能被多次连续迭代 “稀释”。
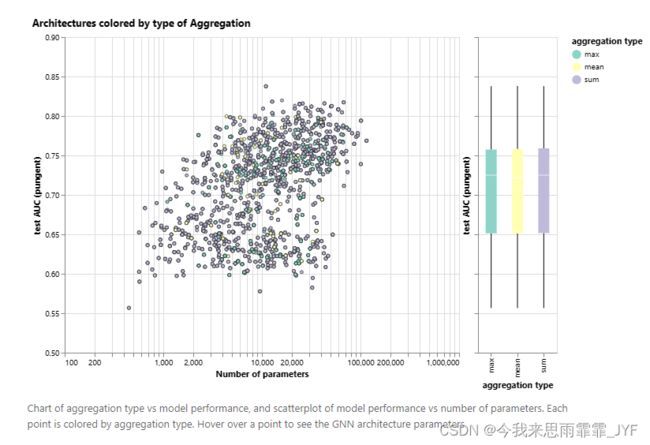
求和比求均值的性能略有提高,但求最大值或求均值也能给出同样好的模型。
总的来说,我们可以看到,交流的图形属性越多,平均模型的性能就越好。我们的任务以全局表示为中心,因此明确学习这一属性也往往会提高性能。
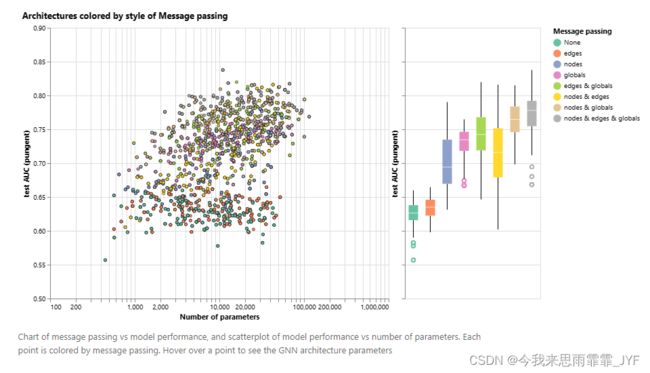
GNN 研究的一个前沿领域不是建立新的模型和架构,而是 “如何构建图形”,更准确地说,是为图形注入可以利用的附加结构或关系。正如我们所看到的,图的属性越多,我们就越能建立更好的模型。在这种特殊情况下,我们可以考虑通过增加节点之间的空间关系、增加非键的边或明确子图之间的可学习关系,使分子图的特征更加丰富。
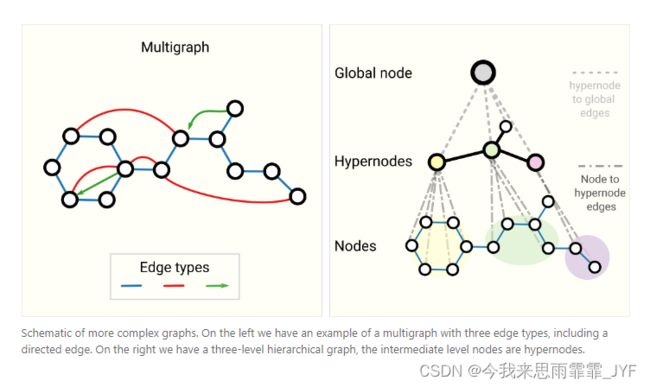
其他类型的图(多图、超图、超节点、层次图)
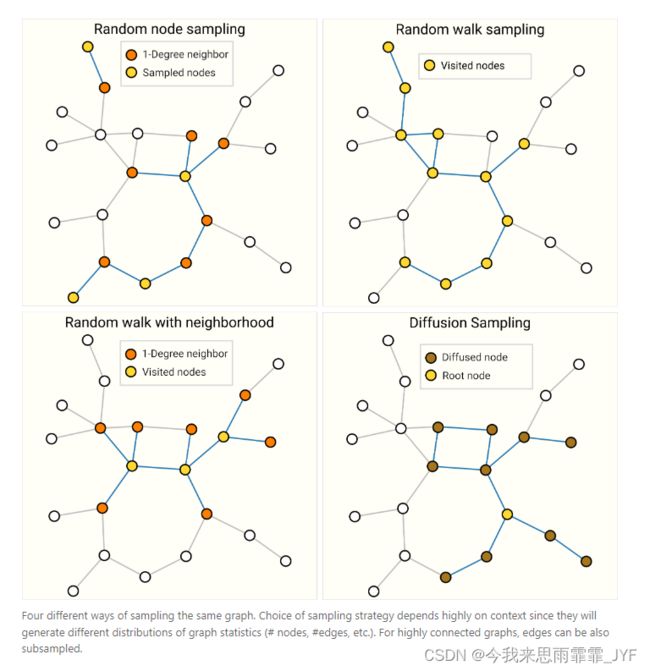
GNN 中的采样图和批处理
总结
GNN 近年来取得的成功为解决各种新问题创造了巨大的机会,图形是一种强大而丰富的结构化数据类型,其优势和挑战与图像和文本截然不同。在本文中,我们概述了研究人员在构建图神经网络方面取得的一些阶段性成果。我们介绍了在使用这些架构时必须做出的一些重要设计选择。