F-DARTS: Foveated Differentiable Architecture Search Based Multimodal Medical Image Fusion

F-DARTS: 基于Foveated可微结构搜索的多模态医学图像融合

注：“Foveated”、“Foveation” 通常指的是一种处理方式，即根据视觉焦点的变化来调整图像处理的方法。

论文链接：https://ieeexplore.ieee.org/document/10145413

项目链接：https://github.com/VictorWylde/F-DARTS

Abstract

多模态医学图像融合(MMIF)在疾病诊断和治疗等领域具有重要意义。由于图像变换和融合策略等人为因素的影响，传统的MMIF方法难以提供满意的融合精度和鲁棒性。现有的基于深度学习的融合方法，由于采用人为设计的网络结构和相对简单的损失函数，在权值学习过程中忽略了人的视觉特征，一般难以保证图像融合效果。为了解决这些问题，我们提出了基于Foveated可微架构搜索(F-DARTS)的无监督MMIF方法。该方法在权值学习过程中引入Foveation算子，充分挖掘人的视觉特征，实现有效的图像融合。同时，通过对互信息、差异关联和、结构相似度和边缘保存值的综合，设计了一种独特的无监督损失函数用于网络训练。基于所提出的foveation算子和损失函数，使用F-DARTS搜索端到端编码器-解码器网络架构以产生融合图像。在三个多模态医学图像数据集上的实验结果表明，F-DARTS的融合效果优于传统的融合方法和基于深度学习的融合方法，融合结果具有视觉上的优越性和更好的客观评价指标。

I. INTRODUCTION

随着医学成像技术的进步，超声成像、计算机断层扫描(CT)、磁共振成像(MRI)、正电子发射断层扫描(PET)和单光子发射计算机断层扫描(SPECT)等不同的成像方式被广泛应用于疾病诊断。每种模式都有自己的优点和缺点。如MRI软组织对比度好，空间分辨率高，但不能很好地显示钙化和骨结构，扫描时间长。CT成像分辨率高，扫描时间短，但组织表征能力有限。多模式医学图像融合(MMIF)可以通过将来自各种成像模式的互补信息集成到综合图像中来帮助准确的疾病诊断和治疗。MMIF的典型应用包括PET-CT融合的区域检测[1]，光声、超声和MR融合成像的图像引导[2]，阻抗光学双峰细胞培养成像的信息融合[3]，靶向前列腺活检的MR-超声融合[4]。

MMIF方法包括传统方法和基于深度学习(DL)的方法。传统算法通过图像变换、活动等级测量和融合规则[5]等组成部分生成融合图像。众所周知的融合算法一般依赖于图像分解[6]-[10]、稀疏表示[11]、[12]、机器学习[13]和形态变换[14]。这些算法大多计算复杂，采用人为设计的图像表示方法和融合规则，影响了融合的效率和质量。

最近，深度学习被用于图像融合，因为融合方法的关键组件可以通过学习深度网络[15]来共同实现。DL已应用于多焦点图像融合[16]-[19]、遥感图像融合[20]、[21]、红外与可见光图像融合[22]-[28]、MMIF[29]-[31]和一般图像融合[32] [36]。这些方法使用卷积稀疏表示(CSR)[32]、卷积神经网络(CNN)[16]-[21]、[25]-[31]、[33]-[36]和生成式对抗网络(GAN)[22]、[24]作为网络骨干，并使用均方误差(MSE)、图像质量评分[34]、感知损失[35]和结构相似性(SSIM)[37]、[38]等度量作为损失函数。

总的来说，上述基于DL的MMIF方法无法获得满意的融合效果，原因有三。首先，这些方法按照图像分类任务的网络框架设计相对固定的网络结构。这样设计的网络不能很好地适应不同医学图像的融合。自动设计适合不同成像方式融合的网络体系结构是较好的选择。其次，这些方法的权值学习过程忽略了人类视觉系统(HVS)的特性，这对医学图像融合至关重要。事实上，在权重学习过程中考虑人的视觉特征以确保融合效果是可取的。最后，需要无监督损失函数，因为MMIF任务没有基本真理。现有的损失函数是单独或简单组合使用强度水平、特征水平和结构水平度量来定义的，因此它们只能在一定程度上探索源图像和融合图像的强度、特征信息和结构信息之间的相关性。设计一个综合的损失函数来保证MMIF过程中的信息保存是非常重要的。

为了解决上述问题，我们提出了一种基于可微分体系结构搜索(DARTS)[39]的无监督MMIF方法，该方法是一种基于梯度的网络体系结构搜索(NAS)[40]方法，在某些计算机视觉任务中比许多其他NAS方法所需的训练时间更少。特别地，提出了一种新颖的Foveated DARTS (F-DARTS)方法来自动生成适合MMIF的网络结构。同时，设计Foveation算子来表示HVS的非均匀分辨率特性之一Foveated[41]，并将其引入到F-DARTS中产生卷积核，从而保证融合效果与HVS的特性相一致。此外，提出了一种有效的无监督损失函数，通过对互补指标的积分来训练F-DARTS，该互补指标可以综合衡量融合结果与两源图像之间的相关性。该方法将灵活的网络结构、Foveation算子和有效的损失函数相结合，保证了良好的融合性能。这项工作的贡献有四方面。

• 在网络结构方面，首次提出了F-DARTS自动识别适合MMIF的网络结构，从而为图像融合网络结构设计提供了一种新的可靠方法。
• 在F-DARTS的核学习方面，在该网络中引入Foveation算子产生卷积核，从而使该网络的融合效果与HVS的特性保持一致。
• 在F-DARTS的损失函数方面，提出了一种独特的无监督损失函数，通过综合表征两个源图像与融合结果之间的相关性的互补度量来保证良好的融合性能。
• 在三个医学图像数据集上评估了我们的方法的性能。主观视觉和定量评价表明，F-DARTS比几种传统的基于深度学习的融合算法具有更好的融合性能。

本文的其余部分结构如下。第二节介绍了现有的图像融合方法。第三部分介绍了F-DARTS的框架、Foveation算子、损失函数和结构搜索。第四节提供了F-DARTS的参数设置以及与其他评估方法的融合性能比较。结论在第五节。

II. RELATED WORKS

A. 融合方法

1) 传统的融合方法 ：在传统的方法中，最流行的算法是基于SR和图像分解的算法。SR融合方法基于信号的自然稀疏性，可分为单分量、多分量和全局三种[42]。单组分方法的灵活性和细节保存性能有限。多分量和全局方法的性能受到稀疏系数融合策略的影响。基于图像分解的方法在空间域或频域工作。前者将源图像的互补信息进行分解，然后对分解后的分量应用特定的融合规则生成融合图像。典型的例子包括基于联合双边滤波和局部梯度能量(JBF-LGE)的方法[43]、基于自适应共生滤波器(ACOF)的方法[44]和自适应双尺度融合(ATF)方法[45]。基于频域的融合方法依赖于多尺度分解。这些方法包括对图像进行不同频段的分解、对分解后的子段进行融合以及对融合后的子带进行逆变换。在图像分解方面，利用小波变换[6]、非下采样轮廓波变换[7]、[10]，剪切波变换 [8]、非下采样剪切波变换[9]等技术将每个源图像分解为低频和高频频段。在频段融合方面，采用参数自适应脉冲耦合神经网络(PAPCNN)对高频频段进行融合，并将基于8邻域的修正拉普拉斯算子加权和与加权局部能量相结合，对低频频段[9]进行融合。利用相位同余性和拉普拉斯能量分别对低频和高频波段进行融合。本文还探索了基于MSD和SR的图像融合方法。Liu等人提出了一种基于多尺度变换和SR的混合融合方案，采用基于SR的方法和最大绝对规则分别融合低频和高频频段。

2) 基于深度学习的融合方法：基于深度学习的融合方法一般包括两种方案。一种方案是使用R3Net[33]和ResNet[23]等模型代替人工设计的方法进行深度特征提取，然后像传统融合方法一样利用这些特征进行图像融合。该方案不能有效地解决融合规则设计的相关问题。另一种方案是使用端到端基于深度学习的融合方案，其中深度学习模型使用标签/源和融合图像之间计算的损失进行训练。对于多焦点图像融合，提出了各种CNN模型[16] [19]。在遥感图像融合方面，提出了FusionCNN[20]和双流融合网络[21]。研究了GAN[22]、[24]、残差网络[25]、密集网络[26]、[27]和NestFuse[28]用于红外和可见光图像融合。其中，DenseFuse[26]将DenseNet的编码功能与CNN的解码功能相结合，使用不同的规则融合特征图。VIFNet[27]利用DenseNet提取特征并使用通道拼接进行融合，并使用加权SSIM和基于MSE的损失函数进行训练。NestFuse[28] 使用类似嵌套结构来增强输入图像的特征提取，以进行图像融合。至于MMIF，很少有基于深度学习的算法是专门为这种情况设计的。Liu等人探索了基于孪生CNN的融合方法。Fu等人提出了一种由特征提取器、融合器和重构器组成的多尺度残差金字塔注意力网络。在[31]中提出了一种多层拼接融合网络，实现了MMIF的特征提取、特征融合和图像重建。此外，基于CSR[32]、FusionDN[34]、图像融合CNN (IFCNN)[35]和U2Fusion[36]等通用融合方法也被应用到MMIF中。FusionDN将源图像连接在一个通道中作为输入，并使用包括SSIM，感知MSE和熵损失在内的损失函数进行网络训练。IFCNN首先利用CNN从源图像中提取显著特征，然后对这些特征进行融合，最后重建融合后的特征进行图像融合。该方法使用从ResNet101计算的MSE损失和感知损失作为损失函数。U2Fusion通过训练基于自适应信息保存度的深度学习模型来实现无监督图像融合。

B. 网络架构搜索

NAS是自动机器学习领域的研究热点。在搜索策略方面，NAS包括基于贝叶斯优化、进化算法、强化学习和梯度[40]的方法。这些方法基本上以两种方式工作。一种方法是首先对结构进行离散采样，然后为每个采样的结构构建一个新的网络，最后对其进行独立训练和评估。缺点是该策略的推理成本较高。

另一种方法是将目标体系结构视为超图的子图，并使搜索空间连续，以保证可以使用梯度下降法对模型的体系结构和权值进行联合优化。一个典型的例子是DARTS。它的搜索空间由多个单元组成，每个单元包含顺序节点。DARTS的工作分为四个步骤。首先，将节点间的操作设置为初始未知。其次，通过在每条边上放置候选操作来完成初始化，从而连续放宽搜索空间。通过初始化，所有的操作将在所有节点之间建立，并组合在一起形成一个概率向量。再次，解决了网络权值与混合概率联合优化的双层优化问题。最后，根据学习到的混合概率生成最优网络权值和网络结构。

近年来，为了提高搜索速度或稳定搜索过程，人们进一步提出了基于可微结构采样器的DARTS方法[46]、部分连通的DARTS方法[47]和基于结构熵正则化器的DARTS方法[48]。然而，现有的DARTS方法主要针对图像分类、目标检测[49]和图像超分辨率[50]等任务进行探索。据我们所知，目前还没有关于使用DARTS的MMIF任务的研究报告。

III. PROPOSED METHOD

A. 基于F-DARTS的图像融合框架

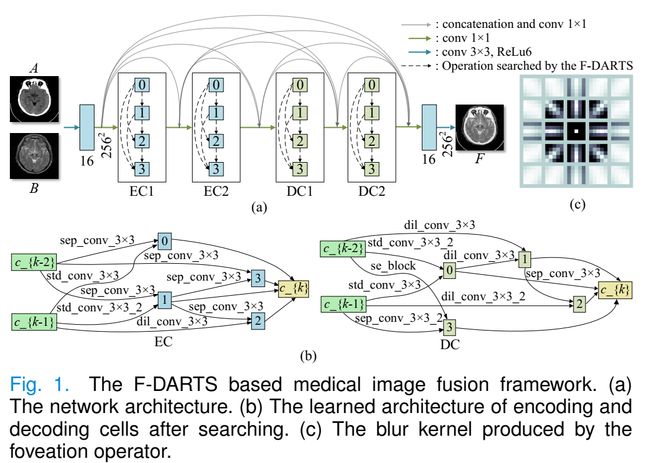
图1显示了基于F-DARTS的融合方法。在这里，F-DARTS与传统的DARTS的不同之处在于其改进的结构和由Foveation算子产生的卷积核。F-DARTS以以下方式从源图像生成融合结果。首先，对两个源图像进行卷积运算，并将得到的卷积图像输入到训练良好的F-DARTS中，其中包括编码器模块(即EC1和EC2)和解码器模块(即DC1和DC2)。其次，通过编码器和解码器模块实现特征提取和重构。最后，对重构图像特征进行卷积运算和在量化表示为6时截断的整流线性单元(ReLu)处理，生成融合结果。

下面将简单解释使用ReLu6而不是ReLu的原因。由于融合图像的强度在[0,1]的范围内，我们需要将激活函数的输出归一化到这个特定的范围内。然而，ReLu的输出范围从0到正无穷，这不仅使直接归一化变得困难，而且容易导致数值爆炸。Mobilenetv2[51]中提出的ReLu6将最大输出限制在6，从而加速了低精度梯度下降的收敛，防止了数值爆炸，增强了十进制表达能力[52]。因此，我们选择ReLu6作为MMIF任务的激活函数，并将其除以6。

图1(a)显示了F-DARTS的结构。FDARTS在原有的基础上进行了改进，将后者改为端到端编解码结构，并将其正常单元和约简单元改为编码单元和解码单元，以确保F-DARTS更适合图像融合任务。所得的F-DARTS由下采样和上采样组件组成，其中前者包括两个编码单元EC1和EC2，而后者包括两个解码单元DC1和DC2。这样的架构是如此灵活，使得编码组件可以提取不同尺度的特征，并且解码组件可以集成这些特征以生成融合的结果。

此外，对不同的cell采用基于通道拼接的密集连接和1×1卷积，以减少网络参数的数量，并保证通过网络学习确定特征映射的组合权值。

F-DARTS的两个细胞的结构如图1 (b)所示。对于EC1, c_{k−1} 和 c_{k−2}分别表示将源图像拼接在一个通道中并在EC1之前经过一个卷积层后的初始状态。对于EC2, c_ {k−1}和c_{k−2}分别表示EC1和上述卷积层的输出。对于DC1和DC2, c_{k−1}和c_{k−2}是前两个单元格的输出。对于F-DARTS的每个单元，其最终输出将是四个节点的串联，其中每个节点表示一个特征映射。

在F-DARTS中，使用Foveation算子生成卷积核。图1©显示了由Foveation算子产生的模糊核，它可以表示HVS的Foveation属性。在权值学习过程中，利用生成的模糊核生成F-DARTS的卷积核。在权值学习中引入Foveation属性确实保证了融合结果与HVS的特性相一致。

B. F-DARTS的细节

1) 用于核学习的Foveation算子：在F-DARTS中，借助基于HVS的Foveation特性设计的Foveation算子来学习卷积核。关于HVS，众所周知，人类可以通过视觉系统获得大约90%的外部信息。通过晶状体后，视觉信息到达视网膜，光信号转化为电信号。这个信号被传递到神经细胞，最后到达大脑皮层。由于视锥细胞和视杆细胞的大小不同，以及视网膜组织分布的不均匀，视网膜中央凹的视锥细胞密度会极高，几乎没有视杆细胞。越靠近视网膜外围，视锥细胞的浓度越低。因此，视网膜图像在视网膜中心部分的清晰度最高，但随着离视网膜中心距离的增加，图像会逐渐模糊。上述现象称为Foveation，可以通过专门设计的Foveation算子再现。如果利用该算子学习F-DARTS中的卷积核，得到的图像融合效果将符合人类的视觉特征。

我们利用Foveation设计了自映射Foveation算子和模糊核，用于非局部均值图像去噪[53]，并将其用于多模态医学图像配准[54]的研究中。在这里，利用Foveation生成模糊核，用于F-DARTS的核学习。根据[53]，我们将考虑patch级别的Foveation，而不是整个图像。对于图像A中的注视点$x$，通过一个patch Foveation算子$O$来实现Foveation：
$$O_x(u)=O[A,x](u)u\in U,\text{\hspace{1em}(1)}$$
其中$U\subset {\mathbb{Z}}^2$表示以原点为中心的邻域，$u$表示在$U$中的一个位置。

为了模拟HVS的Foveation特性，将Foveation算子设计为模糊算子，模糊算子随patch中心的距离而变化。据此，Foveation算子表示为[53]：
$$O_x(u)=\sum _{\xi \in Z^2}A(\xi +x)v_u^{\rho ,\theta }(\xi -u),u\in U,\text{\hspace{1em}(2)}$$
其中，$v_u^{\rho ,\theta }$表示Foveation算子的模糊核，它将基于椭圆高斯概率密度函数(PDF)构建，$\rho$和$\theta$分别决定其轴的伸长和角偏移。显然，算子$O$定义了像素在$u$处的位置，这是通过对$A$中像素$x+u$的邻域施加一个特定的核函数$v_u^{\rho ,\theta }$得到的。这里，$v_u^{\rho ,\theta }$由[53]给出：
$$v_u^{\rho ,\theta }=\{\begin{array}{ll}\sqrt{\mathbf{k}(0)}{g}_{\frac{1}{2\sqrt{\pi }}},& u=(0,0)\\ \sqrt{\mathbf{k}(0)}{g}_{\frac{1}{2\sqrt{\pi }}\sqrt{\frac{\mathbf{k}(0)}{\mathbf{k}(u)}}}^{\rho ,\angle u+\theta },& u\ne (0,0)\end{array}\text{\hspace{1em}(3)}$$
式中，$\sqrt{\mathbf{k}(0)}=\Vert v_u{\Vert }_1$和$\sqrt{\mathbf{k}(u)}=\Vert v_u{\Vert }_2$分别表示窗核$k$的$L_1$范数和$L_2$范数；$g_{\frac{1}{2\sqrt{\pi }}}$表示标准差为$\frac{1}{2\sqrt{\pi }}$的椭圆高斯函数，$\angle u$和$\angle u+\theta$分别表示其轴的角位置和方向。

由Eq.(3)可知，$v_u^{\rho ,\theta }$具有空间变异性，其标准差随距patch中心距离的增加而变化。这样的属性对于$O$模拟HVS的特性Foveation是可取的。参数$\rho$和$\theta$可与$u$组合构成一系列模糊核，形成模糊核块。模糊核$v_u^{\rho ,\theta }$推导为(详见附录)：
$$\begin{array}{rl}& v_u^{\rho ,\theta }=\sqrt{\mathbf{k}(0)}\frac{bk}{\sum bk},\\ & bk=C_4\exp (C_1\cos (2\angle u+2\theta )+C_2\sin (2\angle u+2\theta )+C_3),\end{array}\text{\hspace{1em}(4)(5)}$$
其中$C_1、C_2、C_3、C_4$为常量，$bk$为降采样前的模糊核。

生成的$v_u^{\rho ,\theta }$被引入到权重学习过程中，以生成F-DARTS的卷积核。图2显示了一些模糊内核patch的例子。在这里，各向同性的中心点算子以及径向、手性和切向等各向异性算子通过$\rho$和$\theta$的不同组合产生。然而，本文只考虑各向异性Foveation算子。

在F-DARTS中模糊核的设计涉及两个重要问题。一方面，模糊核的大小应该固定在一个小值（例如，3×3），以确保良好的特征提取性能，但它也会随着$U$的半径$U_r$而变化。因此，模糊核需要从原始核中采样。图3(a)和图3(b)显示了ρ = 2， θ = 0和Ur = 2时原始径向模糊核的采样结果。同时，需要去除冗余的模糊核，以保证模糊核的数量UR (UR= (2Ur +1)²)能够满足F-DARTS的要求。Ur的选择取决于F-DARTS中编码和解码单元的通道数Nc。以Nc = 16为例，要求UR≥16，Ur越小越好。因此，我们选择Ur = 2。相应的，生成25个模糊核，需要去除9个冗余的模糊核。考虑到模糊核的对称性对于有效的特征提取非常重要，并且随着模糊核离中心距离的增加，模糊核对特征提取的影响会减小，因此我们选择在对称性约束下去除远离中心的模糊核。图3©显示了剩余的16个模糊核，其中用红框标记的冗余核已从25个模糊核中删除。

另一方面，我们需要处理F-DARTS的权重计算，这涉及到与现有深度学习网络中类似的反向传播(BP)过程。唯一的区别是F-DARTS的权重将受到Foveation算子的约束。从公式(4)和(5)可知，当ρ固定时(本文选择ρ = 2)， $v_u^{\rho ,\theta }$是θ的函数。因此，F-DARTS的权重是基于其损失函数loss对θ的导数来计算的。根据微分链式法则，$\frac{\partial Loss}{\partial \theta }$为：
$$\frac{\partial Loss}{\partial \theta }=\frac{\partial Loss}{\partial v_u^{\rho ,\theta }}\frac{\partial v_u^{\rho ,\theta }}{\partial \theta },\text{\hspace{1em}(6)}$$
其中，$\frac{\partial Loss}{\partial v_u^{\rho ,\theta }}$按照现有DL网络计算，而$\frac{\partial v_u^{\rho ,\theta }}{\partial \theta }$根据公式(4)、(5)计算为：
$$\begin{array}{rl}& \frac{\partial v^{\rho ,\theta }}{\partial \theta }=\frac{\partial \left(\frac{\sqrt{\mathbf{k}(0)}bk}{\sum bk}\right)}{\partial \theta }=\sqrt{\mathbf{k}(0)}\frac{\frac{\partial bk}{\partial \theta }\sum bk-bk\sum \frac{\partial bk}{\partial \theta }}{{\left(\sum bk\right)}^2},\\ \frac{\partial bk}{\partial \theta }=& C_4(2C_2\cos (2\angle u+2\theta )-2C_1\sin (2\angle u+2\theta ))\\ & \exp (C_1\cos (2\angle u+2\theta )+C_2\sin (2\angle u+2\theta )+C_3).\end{array}\text{\hspace{1em}(7)(8)}$$
在公式(7)中，$\frac{\partial v_u^{\rho ,\theta }}{\partial \theta }$的值是变量，有些是实数，有些是实数矩阵。后者不能通过相同的方法映射为统一的值。为了解决这个问题，我们将使用近似方法来计算θ的值。该方法的实现如下。在F-DARTS训练之前，确定一组θ值的$S_{\theta }$在0^◦到180^◦的范围内，角步长为0.025^◦。该集合中的每个θ值根据式生成相应的模糊核。公式(4)、(5)及其导数值(7)和(8)。在F-DARTS的训练过程中，θ值被初始化。在每次迭代时，根据式(6)中的链式法则计算$\frac{\partial Loss}{\partial \theta }$，并通过BP过程获得更新后的值。为了避免在线计算$v_u^{\rho ,\theta }$和$\frac{\partial v_u^{\rho ,\theta }}{\partial \theta }$，更新后的θ将被更改为$S_{\theta }$中最接近的值。当迭代优化过程结束时，确定最优θ值并得到相应的卷积核。

2) 损失函数：损失函数对于保证融合图像的质量非常重要。理想情况下，损失函数的分量应该有效地度量源图像和融合图像的强度、特征和结构信息之间的相关性。沿着这条线，我们将选择众所周知的融合度量来构建损失函数。现有的融合指标包括基于图像强度的指标，如互信息(MI)和差异相关和(SCD)[55]，基于结构相似性的指标，如SSIM[37]，基于图像特征的指标，如边缘保持度Q^AB/F[56]和人类感知指标。其中，MI表示融合图像中包含的源图像信息量。SCD反映了融合结果与两个源图像之间差异的相关性。SSIM是根据两幅图像之间的亮度、对比度、结构等信息来计算的。Q^AB/F通过局部度量来度量输入图像边缘等显著信息的保存程度。

我们尝试使用每个度量作为F-DARTS的损失函数，并发现在一些定量指标和视觉评价方面，MI、SCD、SSIM和Q^AB/F比其他度量更适合所选多模态医学图像数据集的融合。因此，选择这四个指标并进一步分为两个互补组，其中一组包括MI和SCD，另一组包括SSIM和Q^AB/F。相应地，将F-DARTS的损失函数设计为：
$$Loss={\lambda }_1(L_{MI}+L_{SCD})+(1-{\lambda }_1)(L_{SSIM}+L_{Q^{AB/F}}),\text{\hspace{1em}(9)}$$
其中λ1为两组损失函数的权值。

在基于无监督深度学习的图像配准[57]中，我们将其作为损失函数，将其引入到图像融合任务中，构造相应的损失L_MI为：
$$L_{MI}=1-\frac{MI(A,F)+MI(B,F)}{2},\text{\hspace{1em}(10)}$$
其中$MI(A,F)$计算为：
$$MI\left(A,F\right)=H\left(A\right)+H\left(F\right)-H\left(A,F\right),\text{\hspace{1em}(11)}$$
式中，$H(A)$表示图像A的熵，$H(A,F)$表示图像A和F的联合熵。
$$\begin{gathered} H(X)=-\sum p(x){\log }_{2}p(x), \\ H(X,Y)=-\sum _{x\in \chi }\sum _{y\in y}p(x,y)logp(x,y). \end{gathered}$$
L_SCD的损失计算如下：
$$L_{SCD}=1-SCD=1-\frac{R(F-A,B)+R(F-B,A)}{2},\text{\hspace{1em}(12)}$$
其中R代表相关性[55]。
$$R(D_k,S_k)=\frac{{\sum }_i{\sum }_j(D_k(i,j)-{\bar{D}}_k)({\mathcal{S}}_k(i,j)-{\bar{\mathcal{S}}}_k)}{\sqrt{\left({\sum }_i{\sum }_j(D_k(i,j)-{\bar{D}}_k{)}^2\right)\left({\sum }_i{\sum }_j(S_k(i,j)-{\bar{\mathcal{S}}}_k{)}^2\right)}}$$
L_SSIM损失计算公式为：
$$L_{SSIM}=-\frac{SSIM(A,F)+SSIM(B,F)}{2}.\text{\hspace{1em}(13)}$$
损失$L_{Q^{AB/F}}$计算如下：
$$L_{Q^{AB/F}}=1-Q^{AB/F},\text{\hspace{1em}(14)}$$
其中$Q^{AB/F}$定义为[56]：
$$Q^{AB/F}=\frac{\sum _{m=1}^M\sum _{n=1}^N\left(Q^{AF}(m,n)w^A(m,n)+Q^{BF}(m,n)w^B(m,n)\right)}{\sum _{m=1}^M\sum _{n=1}^N(w^A(m,n)+w^B(m,n))},\text{\hspace{1em}(15)}$$
其中$w^A(m,n)=l^A(m,n)$， $w^B(m,n)=l^B(m,n)$为大小为$m\times n$的两幅源图像的边缘保持权值，$l^A$和$l^B$分别表示A和B的边缘强度；$Q^{AF}$和$Q^{BF}$表示融合结果中边缘相对于两个源图像边缘的保留程度。边缘强度和边缘方向值利用sobel算子：
$$\begin{array}{l}{l}^A(n,m)=\sqrt{s_A^x(n,m{)}^2+s_A^{\nu }(n,m{)}^2}\\ d^A(n,m)={\tan }^{-1}(\frac{s_A^y(n,m)}{s_A^x(n,m)})\end{array}$$
这里，$Q^{AF}$由[56]给出：
$$\begin{array}{rl}{Q}^{AF}(m,n)& =Q_l^{AF}(m,n)Q_d^{AF}(m,n)\\ & =\frac{{\Gamma }_l}{1+e^{{\kappa }_l\left(L^{AF}(m,n)-{\sigma }_l\right)}}\frac{{\Gamma }_d}{1+e^{{\kappa }_d\left(D^{AF}(m,n)-{\sigma }_d\right)}},\end{array}\text{\hspace{1em}(16)}$$
其中${\Gamma }_l、{\Gamma }_d、{\kappa }_l、{\kappa }_d、{\sigma }_l、{\sigma }_d$为常数；$Q_l^{AF}(m,n)$和$Q_d^{AF}(m,n)$分别表示边缘强度$l$和边缘方向$d$的保存值；$L^{AF}(m,n)$和$D^{AF}(m,n)$分别为相对边缘强度和边缘方向值。需要注意的是，公式(14)不是导数，因为$Q^{AF}$和$Q^{BF}$的计算涉及到源图像和融合图像边缘方向差的绝对运算。为了解决这个问题，在PyTorch[17]中采用了通用autograd策略，以确保$L_{Q^{AB/F}}$在网络训练期间可以有效地反向传播。

3) F-DARTS的结构搜索：在FDARTS中，EC和DC的单元搜索过程相同，尽管它们的单元结构不同。至于EC和DC的个数，选择较少的EC和DC会比较好，因为图像融合是一个复杂度相对较低的问题，不需要大量参数的网络。在本文中，我们选择了两个EC和两个DC，因为我们通过实验发现，引入更多的EC和DC只会以增加网络复杂性为代价，在融合结果的定量度量方面提供很小的改进。同时，我们将EC和DC中的节点数固定为4个，将EC2和DC1的初始化通道数固定为16个，将EC1和DC2的初始化通道数固定为8个。这样的设置意味着EC2和DC1中的每个节点以及EC1和DC2中的每个节点分别代表16通道和8通道的特征映射。因为每个单元的输出包括四个节点，EC2和DC1都将产生64个特征映射，这表示F-DARTS中的最大通道数。以上设置可以帮助生成轻量级的F-DARTS。

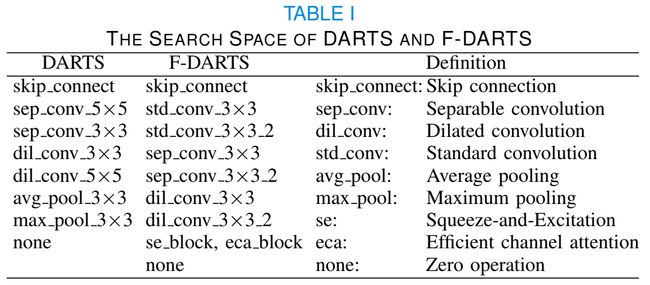
F-DARTS的搜索空间已经重新设计，如表1所示，其中std conv 3×3表示使用3×3内核的标准卷积，std conv 3×3_2表示标准卷积重复级联两次，其他操作也可以类似地解释。与传统的DARTS相比，F-DARTS的搜索空间保留了零操作“none”和跳跃连接“skip connect”，以便于寻找更稳定的结构，同时删除了所有池化层，增加了标准卷积“std conv”，使结构更加多样化。此外，我们将所有5×5卷积核改为两个3×3卷积核，以减少参数的数量，并在Squeeze-and-Excitation网络(SE-Net)[58]中引入了“SE块”和有效通道注意网络(ECANet)[59]中引入了“ECA块”等注意模块，因为它们可以利用通道注意机制有效增强图像特征。

基于上述网络框架和重新设计的搜索空间，进行F-DARTS的架构搜索。该过程包括结构概率$\alpha$和网络权值$W$的优化。$\alpha$的优化是确定cell中节点之间的操作。对于两个节点$(i,j)$之间的每个操作$o^{(i,j)}(f)$，将使用softmax函数将所有操作连接为[39]：
$${\bar{o}}^{(i,j)}\left(f\right)=\sum _{o\in \mathcal{O}}\frac{\exp \left({\alpha }_o^{(i,j)}\right)}{{\sum }_{o^{\prime }\in \mathcal{O}}\exp \left({\alpha }_{o^{\prime }}^{(i,j)}\right)}{o}^{(i,j)}\left(f\right),\text{\hspace{1em}(17)}$$
式中，$f$为特征映射；$O$表示候选操作的集合，这些候选操作对应于我们提出的F-DARTS的搜索空间。

对于一对节点$(i,j)$，我们将使用维数$|O|$的向量$\alpha (i,j)$来参数化混合权重的操作。相应地，通过交替优化$W$和$\alpha$，可以得到最优的$\alpha$。这样的搜索过程可以描述为：
$$\begin{array}{rl}& \underset{\alpha }{\min }Los{s}_{val}\left(W^{\ast }\left(\alpha \right),\alpha \right)\\ & s.t.W^{\ast }\left(\alpha \right)=\underset{W}{\mathrm{argmin}}Los{s}_{train}\left(W,\alpha \right),\end{array}\text{\hspace{1em}(18)}$$
由公式(18)可知，F-DARTS的架构搜索实际上是一个双层优化问题。优化包括最小化训练集上的$Los{s}_{train}(W,\alpha )$以确定最优权值，最小化$Los{s}_{val}(W^{\ast }(\alpha )，\alpha )$在验证集上确定基于最优权重的最优$\alpha$。在这里，$Los{s}_{val}(W^{\ast }(\alpha ),\alpha )$和$Los{s}_{train}(W,\alpha )$通过分别计算它们对$\alpha$和$W$的导数来同时实现。需要注意的是，$\frac{\partial Los{s}_{train}(W,\alpha )}{\partial W}$是由公式(6)-(8)计算的。

基于公式(18)产生的最优$\alpha$表示节点之间所有操作的概率。为了实现有效的网络结构搜索，将对网络进行进一步的修剪。对于每个单元中的任意两个节点，只选择权重最高的两个操作作为它们之间的操作。这样就可以得到最终的最优$\alpha$。在最优$\alpha$的基础上，通过最小化训练集上公式(18)中的$Los{s}_{train}(W,\alpha )$得到最终最优W。

IV. EXPERIMENTAL RESULTS

A. 实验设置

1) 数据集：使用Atlas、BrainWeb和回顾性图像配准评估(RIRE)数据集对F-DARTS进行评估。Atlas数据集[60]包括哈佛医学院收集的不同疾病的人脑CT、MR、PET和SPECT图像。BrainWeb数据集[61]包括由MRI模拟器生成的MR体积数据。RIRE数据集[62]包括CT-MR和PETMR图像对。表2显示了为三个数据集生成的训练、验证和测试集的详细信息。

对于Atlas数据集，我们获得了三组图像，包括797对多模态MR (MM)图像对，282对CT-MR (CM)图像对和540对CT/MR-SPECT (CMS)图像对。对于每一组图像对，我们将按8:1:1的比例随机分为训练集、验证集和测试集。对训练集中的256×256源图像进行32步采样处理，将每个源图像截取成多个128×128图像，然后进行平移，对生成的部分图像进行任意角度的翻转或旋转，从而得到最终的训练集。同样，我们得到了三个验证集和三个测试集，都是随机选择的60 MM图像对，增强56 CM图像对和54 CMS图像对。

对于BrainWeb和RIRE数据集，我们将使用与Atlas数据集类似的数据论证方法来生成所需的数据，如表2所示。需要注意的是，首先使用基于模态独立邻域描述符(MIND)的方法[63]对RIRE数据集中的图像对进行配准，然后使用配准后的图像对生成训练集、验证集和测试集。

2) 比较方法：将F-DARTS与传统算法PAPCNN[9]、JBFLGE[43]、ACOF[44]和A TF[45]以及基于DL的方法DenseFuse[26]、VIFNet[27]、NestFuse[28]、IFCNN[35]和U2Fusion[36]进行比较。传统方法首先选取相关参数作为建议值，然后对其进行调整，得到不同数据集的良好融合图像。对于基于深度学习的方法，VIFNet和U2Fusion是在上述三个数据集上进行训练的，而DenseFuse、NestFuse和IFCNN则直接用于MMIF，因为它们由相应的作者进行了充分的训练。

3) 融合指标：使用10个指标来评估F-DARTS和比较算法的融合性能，即MI，MI在小波变换生成的特征图像(FMI_w)上计算，融合伪影N^AB/F[64]、Q^AB/F[56]、基于相似性的度量(Q_S)[65]、SCD[55]、Chen-Blum度量Q_CB[66]、融合的视觉信息保真度(VIFF)[67]、空间频率误差比(rSFe)[68]和标准差(SD)。采用这些指标是因为它们在评估图像融合质量方面的普及和有效性。N^AB/F测量引入融合图像的伪影。Q_S计算为融合图像和源图像中两对局部区域的加权或更大的SSIM值。Q_CB作为质量图的平均值计算，该质量图是使用显著性图对对比度保持图进行加权产生的，这些对比度保持图是由滤波源和融合图像上计算的局部对比度图生成的。VIFF是基于视觉信息保真度计算的[69]。rSFe定义为从源图像计算得到的空间频率误差(SF)与参考频率的比值，其中SF误差表示融合结果的SF与参考频率的差值。负的rSFe表示丢失了有意义的信息，而正的rSFe表示在图像融合过程中引入了噪声或信息失真。SD测量图像强度在平均值周围的变化。MI、FMIw、Q^AB/F、VIFF、Q_S、Q_CB、SD值越大，N^AB/F、|rSFe|值越小，融合质量越好。

B. 消融研究

F-DARTS是在Ubuntu 16.04上使用Pytorch 1.2.0实现的，并在具有Intel酷睿i7-6950X CPU和96G RAM的计算机上实现。为了加速我们的方法的训练，使用了带有CUDA 10.1的NVIDIA GTX 1080Ti GPU。采用Adam优化器对体系结构概率和网络权重进行优化。我们方法的训练模型的使用可以在https://github.com/VictorWylde/F-DARTS上找到。在这里，我们将讨论F-DARTS中λ1的选择及其相对于DARTS和专门设计的结合DenseNet和CNN的网络(简称DsCNN)的优势。

1) λ1的确定：在基于无监督学习的F-DARTS中，损失函数的构成对融合结果影响很大。对于λ1，根据损失函数的四个分量和融合结果的融合指标得到其最优值。需要注意的是，在消融研究中，一旦λ1发生变化，我们就会寻找新的对应网络，以保证不同λ1值的融合效果最好。

图4显示了不同λ1对Atlas数据集中CMS图像对的F-DARTS训练和验证曲线。显然，对于不同的λ1值，F-DARTS可以收敛。λ1越大，Q^AB/F和SSIM越小，而MI和SCD越大。因此，如果非常重视两个源图像中细节和结构信息的保存，则相对较小的λ1是可取的。

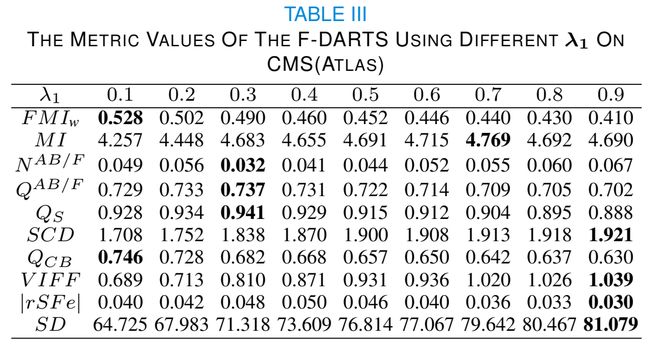
为了进一步确定最佳λ1，在表3、4、5所示的三个数据集上计算不同λ1的F-DARTS的度量值。一般来说，我们的方法在λ1 = 0.3时提供了最高或极具竞争力的FMIw, MI, Q^AB/F, Q_S, Q_CB和最低的N^AB/F。当λ1 = 0.9时，SCD、VIFF、SD值最高，|rSFe|值最低。由于这些指标的变化趋势不一致，最好选择λ1=0.3，以在所有指标之间实现良好的权衡。

2) F-DARTS、DARTS和DsCNN的比较：为了证明F-DARTS中Foveation算子的有效性及其结构的优越性，我们将在三个数据集上将我们的方法与DARTS和DsCNN进行比较。DsCNN也由编码和解码层组成，如图5所示。在这里，每个编码层是一个最大通道数为64的DenseNet，而每个解码层是一个由多个卷积层组成的上采样结构。为了确保比较的DsCNN与涉及两个编码单元的F-DARTS之间的相似性，我们还在DsCNN的编码层使用了两个密集块，其中每个密集块具有与DenseFuse相同的结构，但通道数量略有不同。对于DARTS和DsCNN，它们将使用与F-DARTS相同的损失函数进行网络训练。

为了验证F-DARTS相对于DARTS的优势，将比较它们的梯度加权类激活映射(GradCAM)[70]。Grad-CAM根据流向最终卷积层的类特定梯度信息生成粗定位图，以突出显示重要的图像区域。图6显示了在Atlas数据集中的CT-MR和多模态MR图像对上运行的DARTS和F-DARTS中的EC1的Grad-CAM。显然，在图6(a2)和图6(b2)中，DARTS忽略了一些相对较弱的细节，并且在图6(a3)和图6(b3)中相应的颜色表示源图像中一些较强的细节没有得到重视。相比之下，F-DARTS可以有效地突出弱细节，而对强图像细节具有重要意义，因为它们在相应的Grad-CAM中具有几乎最亮的颜色。在权值学习中引入了Foveation算子，保证了F-DARTS可以充分利用人的视觉特征来进行有效的MMIF。

表六显示了三个测试集上的DARTS、DsCNN和F-DARTS的度量值。定量评价表明，除了DsCNN在CMS(Atlas)和MM(BrainWeb)上产生的|rSFe|小于F-DARTS外，F-DARTS在几乎所有指标上都优于DARTS和DsCNN，与我们在CMS(Atlas)和MM(BrainWeb)上的方法相比，DARTS提供了略高的FMIw、Qs和MI。

图7显示了Atlas数据集中CTMR和MR-SPECT图像对中选择的感兴趣区域(ROI)上的DARTS、DsCNN和F-DARTS的融合结果。对于CT-MR图像融合，DARTS在图7(a3)中黄色圆圈所标记的明亮细节周围产生不希望的信息。DsCNN的性能比F-DARTS差，因为它破坏了图7(a4)中用绿色、红色和黄色圆圈标记的图像细节。在MRSPECT图像融合中，将SPECT图像作为RGB图像转换为YUV颜色空间。利用每种融合方法对MR图像和Y通道进行融合，并将融合结果与U通道和V通道相结合，得到融合YUV图像。将YUV图像转换为RGB颜色空间，得到最终的融合结果。如图7(b3-b5)所示，F-DARTS可以产生比DARTS和DsCNN方法更高清晰度的融合图像细节。

C. 定性评价

图8和图9分别显示了所有评估方法对Atlas和RIRE数据集的CTMR图像对的融合结果。从图8中可以看出，除了ACOF和VIFNet之外，所有评估方法在红框所标记的部分区域都造成了强度不一致。ACOF和其他基于深度学习的方法在保留MR图像中的明亮细节方面表现不佳，如蓝框所示。IFCNN、NestFuse和U2Fusion会降低融合结果中某些边缘的亮度和对比度。相比之下，F-DARTS提供了更好的细节保存，并产生更清晰的融合图像，具有较高的边缘清晰度和亮度。此外，从图9可以看出，PAPCNN在一定程度上导致了图像细节的模糊。ACOF、IFCNN和U2Fusion方法在融合后的图像中引入了明显的伪影。DenseFuse和VIFNet方法对MR图像的细节产生不同程度的亮度降低。我们的方法可以避免伪影，为图像细节提供高亮度，并且可以比所有其他方法更好地保留图9(b10)中红色箭头标记的边缘。

图10和图11分别显示了所有评估方法在MM(Atlas)和MM(BrainWeb)上的融合图像。如图10(b1)-(b4)所示，四种传统方法在融合图像中产生不连续的边缘和一些不需要的伪影。其他基于深度学习的方法会导致图10(a2)中三个红框标记的重要图像细节丢失，并严重损坏两个绿框标记的边缘。F-DARTS比这些方法更有效地保留了两个源图像的细节，产生的融合结果具有更高的亮度和对比度，更符合HVS的特点。此外，从图11中可以看出，我们的方法在保留图11(a2)中四个红框和蓝框标记的图像细节方面优于其他比较方法。

此外，我们还将在图12中比较所有评估方法在MR-SPECT图像对上产生的融合图像。从图12(b1-b9)可以看出，其他方法不能很好地保留重要的图像细节，也不能很好地保持某些边缘的清晰度，如红色框和黄色框所示。如图12(b5)、12(b6)、12(b8)和12(b9)中的蓝框所示，DenseFuse、VIFNet、NestFuse和U2Fusion对源MR图像中的一些细节有不同程度的破坏。IFCNN产生的融合图像存在不良伪影。通过比较，F-DARTS将MR图像中的细节与SPECT图像的色度和亮度有效地融合到融合结果中，得到了边缘保持更好、清晰度更高、信息更丰富的融合图像。

D. 定量评价

为了定量评价所有融合方法的性能，在CM(Atlas)、MM(Atlas)、CMS(Atlas)、CM(RIRE)和MM(BrainWeb)五个测试集上计算10个指标。对于各种方法的每个指标，其均值和标准差列于表7。这里，每个指标的最佳平均值用粗体标记。标准偏差衡量的是每个指标的所有值与其平均值之间的离散度。标准差越小，数据越集中。表7显示，我们的方法提供了比其他方法更高的平均FMIw、MI、Q^AB/F、Q_S、SCD、VIFF和SD。在所有方法中，它在N^AB/F和Q_CB方面排名第二，在|rSFe|方面排名第四。与大多数评价方法相比，F-DARTS对N^AB/F、Q_S、SCD、Q_CB和SD的标准偏差较小。

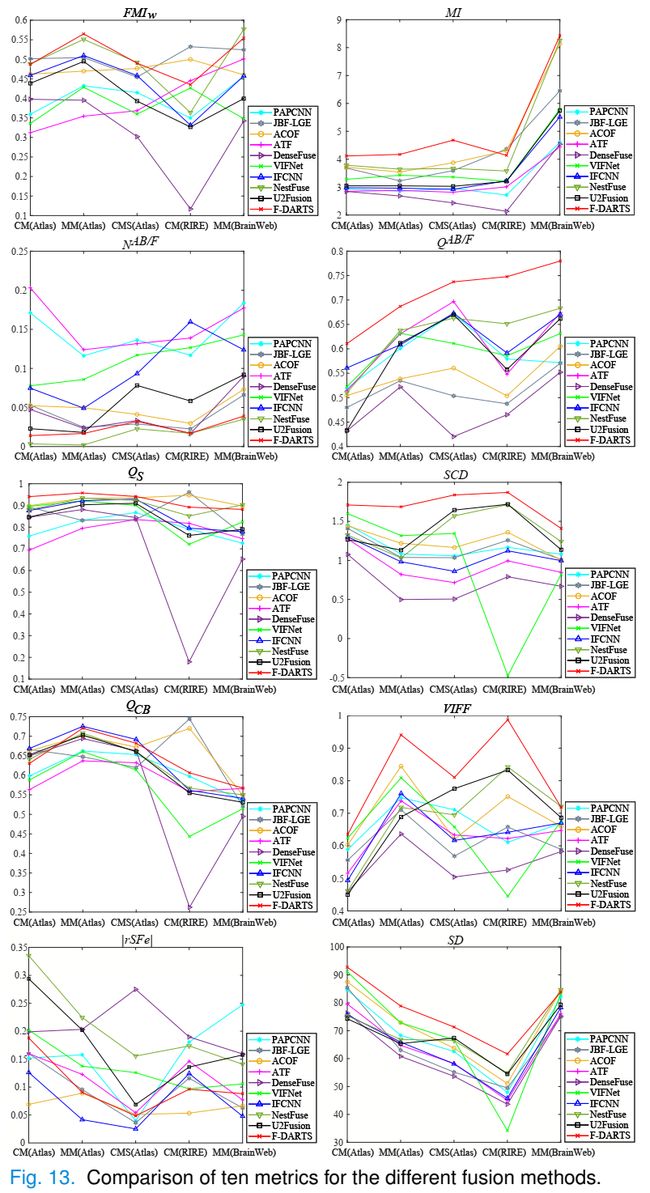
图13显示了每个测试集上各种方法的十个指标。显然，在所有方法中，F-DARTS在所有测试集中始终记录最高的Q^AB/F、SCD、VIFF和SD。除了在CM(RIRE)上优于JBFLGE、ACOF和ATF方法外，F-DARTS提供了最具竞争力的价值。至于MI，除了CM(RIRE)之外，F-DARTS在5个测试集上的表现优于其他方法，其中JBF-LGE和ACOF方法的表现优于我们的方法。对于N^AB/F, F-DARTS在所有方法中基本上排名第二或第三。此外，F-DARTS在Atlas数据集上提供了最高的Q_S值，在MM(Atlas)、CMS(Atlas)和MM(BrainWeb)上提供了最高或第二高的Q_CB值，并且在MM(Atlas)和CM(RIRE)上提供了几乎第二小的|rSFe|值。

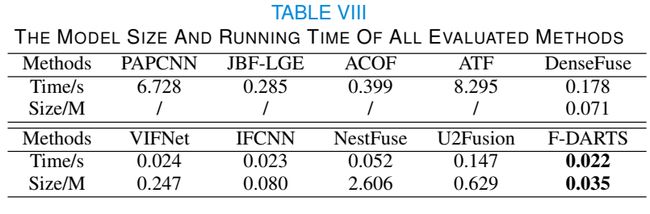
E. 模型复杂性和实现效率

在这里，我们将比较表8中所有评估方法的模型复杂性和实现效率。显然，F-DARTS在所有DL模型中具有最小的尺寸。同时，我们的方法在所有被评估的方法中实现效率最高，其运行时间约为PAPCNN的1/300，约为DenseFuse的1/8。

V. CONCLUSION

本文提出了一种基于可微结构搜索的MMIF无监督学习框架。由于采用以下策略，所提出的方法具有优越的融合性能。首先，我们提出了基于F-DARTS的寻优策略来寻找适合MMIF的可靠网络结构。自动搜索生成有效的编解码器结构和网络权值。其次，将Foveation算子引入到F-DARTS的权值学习中。Foveation算子能很好地再现HVS的Foveation特性，有助于有效地生成卷积核，保证融合图像的质量。最后，我们设计了一个无监督损失函数，它不需要融合图像的基础真理。所设计的损失函数包含了多种互补的度量，可以衡量融合图像与源图像在强度、结构信息和边缘信息方面的相关性。

对多模态MR图像、CT-MR图像和CT/MR-SPECT图像的定量和定性评估表明，与几种传统的基于DL的融合算法相比，我们的方法具有优越的融合性能。未来的工作将集中于为损失函数设计更有效的视觉感知度量，并将我们的方法扩展到三维医学图像融合。

APPENDIX

$v_u^{\rho ,\theta }$的计算

基于工作[53]，[71]，我们将提供计算模糊核$v_u^{\rho ,\theta }$的详细算法。对于$v_u^{\rho ,\theta }$，其计算依赖于窗核$k$，定义为[71]：
$$\begin{array}{rl}& \mathbf{k}=1-{\left(\frac{0.67568}{\sqrt{2}{U}_r}l2d\right)}^{0.059079081},\\ & l2d_{m,n}=\sqrt{{\left(s{1}_{m,n}-U_r-1\right)}^2+{\left(s{2}_{m,n}-U_r-1\right)}^2},\end{array}\text{\hspace{1em}(19)(20)}$$
其中$Ur$为patch的半径，$s2$和$s1$由meshgrid函数生成：
$$[s2,s1]=\text{meshgrid}(-U_r:U_r,-U_r:U_r).\text{\hspace{1em}(21)}$$
对于核$k$，其L1范数$wl1$计算为[72]：

$$wl1=\sqrt{\frac{-2\pi }{\ln (1-p)}\mathbf{k}(0)}=\sqrt{\frac{-2\pi }{\ln (1-(1-e^{-2\pi }))}\mathbf{k}(0)}=\sqrt{\mathbf{k}(0)},\text{\hspace{1em}(22)}$$
其中$p=1-e^{-2\pi }$是常数。

优化目标$oTT$为：
$$oTT=\min (\mathbf{k}(0),\max (\frac{\mathbf{k}}{\sum \mathbf{k}},\frac{\mathbf{k}(0)}{{\left(2U_r+1\right)}^2})),\text{\hspace{1em}(23)}$$
其中$\min (\cdot )$和$\max (\cdot )$分别表示最小和最大算子。

根据$wl1$和$oTT$，迭代优化初始化矩阵$vsI$计算为：
$$vsI=\frac{wl1}{2\sqrt{\pi \cdot oTT}}=\frac{\sqrt{\mathbf{k}(0)}}{2\sqrt{\pi \cdot oTT}}=\frac{1}{2}\sqrt{\frac{\mathbf{k}(0)}{\pi \cdot oTT}}.\text{\hspace{1em}(24)}$$
基于vsI，我们将实现以下迭代优化，以获得最终的模糊核。

步骤1：将$vsI$中$u_1,u_2$处的初始值$vs$设为$vs=ct\cdot vsI(u_1,u_2)$，其中$ct$为随迭代优化过程变化的系数。

步骤2：每次迭代计算非归一化椭圆高斯模糊核$bk$。
$${\theta }_p=\angle u+\theta =\mathrm{atan}2\frac{U_r-u_2+1}{U_r-u_1+1}+\theta ,\text{\hspace{1em}(25)}$$
式中${\theta }_p$为$bk$与patch的主轴之间的旋转角度，atan2计算方位角。

基于${\theta }_p$和meshgrid创建的过采样旋转网格$g_1$和$g_2$，切向旋转网格$gT$和径向旋转网格$gR$计算为[71]：
$$\{\begin{array}{l}gT=g_2\cos {\theta }_p-g_1\sin {\theta }_p,\\ gR=g_2\sin {\theta }_p+g_1\cos {\theta }_p.\end{array}\text{\hspace{1em}(26)}$$
设$ST=\frac{vs}{\sqrt{\rho }}$和$SR=vs\sqrt{\rho }$。在过采样的旋转网格上计算$bk$为：
$$\begin{array}{rl}bk=& \frac{\exp (-(\frac{g{T}^2}{2S{T}^2}+\frac{g{R}^2}{2S{R}^2}))}{2\pi \cdot ST\cdot SR}\\ =& \begin{array}{r}\frac{1}{2\pi v{s}^2}\exp (-\frac{1}{2v{s}^2\rho }({\rho }^{2}g{T}^2+g{R}^2))\end{array}\\ =& C_4\exp (C_1\cos (2\angle u+2\theta )+C_2\sin (2\angle u+2\theta )+C_3)\end{array}\text{\hspace{1em}(27)}$$
其中
$$\begin{array}{rl}& C_1=\begin{array}{r}\frac{({\rho }^2-1)(g_1^2-g_2^2)}{4\rho v{s}^2}.\end{array}\\ & C_2=\begin{array}{r}\frac{({\rho }^2-1)g_1{g}_2}{2\rho v{s}^2}.\end{array}\\ & C_3=\begin{array}{r}-\frac{({\rho }^2+1)(g_1^2+g_2^2)}{4\rho v{s}^2}.\end{array}\\ & C_4=\frac{1}{2\pi v{s}^2}.\end{array}\text{\hspace{1em}(28)(29)(30)(31)}$$
步骤3：下采样$bk$为：
$$bk=bk(\frac{oF+1}{2}:oF:(dim-\frac{oF-1}{2}),\frac{oF+1}{2}:oF:(dim-\frac{oF-1}{2})),\text{\hspace{1em}(32)}$$
其中$oF$表示预定义为5的过采样因子，$dim$表示$bk$中的行/列数。

步骤4：计算$v_u^{\rho ,\theta }$为：
$$v_u^{\rho ,\theta }=\sqrt{\mathbf{k}(0)}\frac{bk}{\sum bk}.\text{\hspace{1em}(33)}$$
步骤5：计算$v_u^{\rho ,\theta }$的$L_2$范数$bl2$的平方：
$$bl2(u_1,u_2)=\sum v_u^{\rho ,\theta }\cdot v_u^{\rho ,\theta }.\text{\hspace{1em}(34)}$$
步骤6：确定$bl2$和$oTT$之间的差异，如果该差异小于预定义值，则停止优化以输出最终的$v_u^{\rho ,\theta }$。否则，请执行步骤2。