算法通关村第一关——链表经典问题之寻找公共子节点笔记
链表之公共子节点问题
1、问题描述
本题是业界里一本经典的算法书《剑指offer》中的一道题,在原书中问题描述如下:
2、题目样例
回顾一下链表的定义,不难知道,本题要求的是找出下图中用方框框住的部分
- 输入:listA = [4,6,8,1,2]、listB = [3,9,1,2]
- 输出:firstCommonNode = 1
链表A中的node(8)和链表B中的node(9)共同指向了node(1),所以node(1)就是我们最终要找的第一个公共节点。
3、解题思路
当一个问题来了,该如何解决呢?一般在算法的解题中,主要运用的是常见的数据结构和常用的算法思想,把这些都想一遍,看看用什么能将问题解决。
常见的数据结构有数组、链表、队列、栈、Hash、集合、树、堆、图。
常用的算法思想有查找、排序、双指针、递归、迭代、分治、贪心、回溯和动态规划等。
再回到本题,首先想到的就是蛮力法,结合冒泡排序的思想,将其中一个链表的节点依次去与另一个链表的节点相比较,当出现相同的节点的时候,就是我们题目中需要的节点。但是这种方法虽然简单,但是时间复杂度比较高,在面试中将其作为最终方案的话比较low,直接pass。
再来看Hash,先将一个链表完全存入到Map中,再一边遍历第二个链表,一边检测遍历到的节点是否再Hash中,如果两个链表存在公共节点,那就能在Map中找到。集合跟Hash一样用,这种思路对Hash适用,所以对集合也适用,这样就又多出来两种方案。这两种方案是基于Hash的,所以时间复杂度很低,只有O(1),但是因为要另外存储一个链表,所以空间复杂度达到了O(n)。
既然想到了用空间换时间,那其他的开辟空间的方法呢?来看队列和栈,队列由于是先进先出的结构,所以在这里没啥用,不过栈是先进后出的,所以我们可以把两个链表分别压入两个栈中,之后一边同时出栈,一边比较出栈的节点是否相同,如果相同则说明两个链表存在相交的节点,那么最后一个出栈的相同节点就是我们要找的那个节点。
虽然Hash和栈解决了这个问题,但是额外开辟了O(n)的空间,那么有没有只用一两个变量就能解决问题的方法呢?答案是有的。
比如下面两种方法:
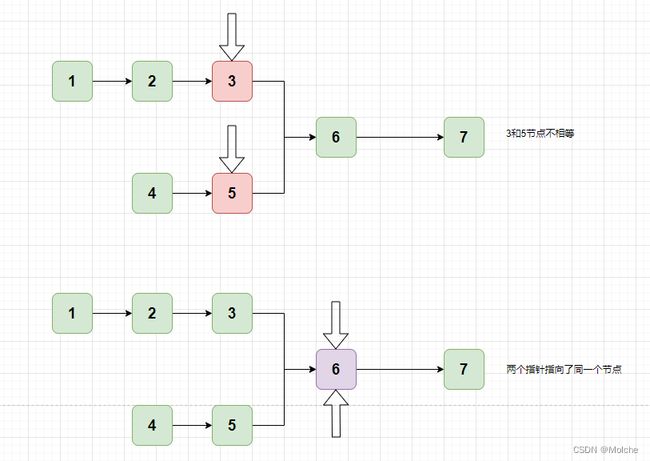
第一种是利用双指针的思想,结合链表长度的差值来达到一个错位相等的情况,如下图:
我们先将两个表都遍历一遍,上面一个链表的长度为5,下面一个链表的长度为4,两者相差为1(设为K)个。我们再使用两个指针,分别指向链表的头部,让长一点的链表先走K=1步,这样就相当于指针后面的链表等长了。
然后我们再比较指针指向的两个节点,如果相同则是我们需要的结果,如果不同就继续往下移,直到指向null。
虽然这种方法用到的空间不多,但是如果公共节点在最后一个,一个链表的长度为m,另一个链表的长度为n,先遍历得到长度需要的时间就是m+n,后面比较结果的时候,因为要移到最后一个节点,所以又用了m+n的时间,最后的时间复杂度是O(2*(m+n))。
有没有更好的一种方法,让我们来看最后一种方案:
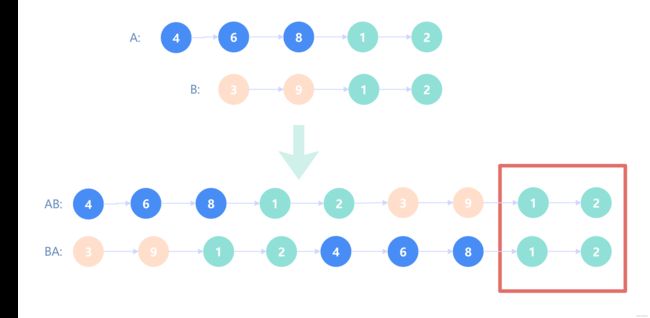
最后一种方法是拼接字符串,如下图:
我们可以这样理解,假设A、B链表存在公共子节点,链表A在公共子节点左侧的部分为leftA、右侧的部分为rightA,链表B在公共子节点左侧的部分为leftB、右侧的部分为rightB,因为公共子节点的右侧部分是相等的,所以rightA=rightB,有了这些前提条件,我们再来看刚刚拼接起来的链表
- AB = leftA + rightA + leftB + rightB
- BA = leftB + rightB + leftA + rightA
所以分别遍历AB和BA就能从某个位置开始恰好就找到了相交的点,即第一个公共子节点。
这里可以进一步优化一下,如果建立新的链表太浪费空间了,我们只要在每个链表访问完之后,将指针调整到另一个链表的表头继续遍历即可。
4、代码实现
解题的思路出来了,写代码就很容易了,只需要注意一些边界值的情况就好
4.1 哈希
/**
* 方法1:通过Hash辅助查找
*
* @param pHead1
* @param pHead2
* @return
*/
public static ListNode findFirstCommonNodeByMap(ListNode pHead1, ListNode pHead2){
if (pHead1 == null || pHead2 == null) {
return null;
}
ListNode current1 = pHead1;
ListNode current2 = pHead2;
HashMap<ListNode, Integer> hashMap = new HashMap<ListNode, Integer>();
while (current1 != null) {
hashMap.put(current1, null);
current1 = current1.next;
}
while (current2 != null) {
if (hashMap.containsKey(current2))
return current2;
current2 = current2.next;
}
return null;
}
4.2 集合
/**
* 方法2:通过集合来辅助查找
*
* @param headA
* @param headB
* @return
*/
public static ListNode findFirstCommonNodeBySet(ListNode headA, ListNode headB) {
Set<ListNode> set = new HashSet<>();
while (headA != null) {
set.add(headA);
headA = headA.next;
}
while (headB != null) {
if (set.contains(headB))
return headB;
headB = headB.next;
}
return null;
}
4.3 栈
/**
* 方法3:通过栈
*/
public static ListNode findFirstCommonNodeByStack(ListNode headA, ListNode headB) {
Stack<ListNode> stackA = new Stack();
Stack<ListNode> stackB = new Stack();
while (headA != null) {
stackA.push(headA);
headA = headA.next;
}
while (headB != null) {
stackB.push(headB);
headB = headB.next;
}
ListNode preNode = null;
while (stackB.size() > 0 && stackA.size() > 0) {
if (stackA.peek() == stackB.peek()) {
preNode = stackA.pop();
stackB.pop();
} else {
break;
}
}
return preNode;
}
4.4 双指针差值
/**
* 方法4:通过差值来实现
*
* @param pHead1
* @param pHead2
* @return
*/
public static ListNode findFirstCommonNodeBySub(ListNode pHead1, ListNode pHead2) {
if (pHead1 == null || pHead2 == null) {
return null;
}
ListNode current1 = pHead1;
ListNode current2 = pHead2;
int l1 = 0, l2 = 0;
while (current1 != null) {
current1 = current1.next;
l1++;
}
while (current2 != null) {
current2 = current2.next;
l2++;
}
current1 = pHead1;
current2 = pHead2;
int sub = l1 > l2 ? l1 - l2 : l2 - l1;
if (l1 > l2) {
int a = 0;
while (a < sub) {
current1 = current1.next;
a++;
}
}
if (l1 < l2) {
int a = 0;
while (a < sub) {
current2 = current2.next;
a++;
}
}
while (current2 != current1) {
current2 = current2.next;
current1 = current1.next;
}
return current1;
}
4.5 拼接链表
/**
* 方法5:通过序列拼接
*/
public static ListNode findFirstCommonNodeByCombine(ListNode pHead1, ListNode pHead2) {
if (pHead1 == null || pHead2 == null) {
return null;
}
ListNode p1 = pHead1;
ListNode p2 = pHead2;
while (p1 != p2) {
p1 = p1.next;
p2 = p2.next;
if (p1 != p2) {
if (p1 == null) {
p1 = pHead2;
}
if (p2 == null) {
p2 = pHead1;
}
}
}
return p1;
}
5、总结
本道题主要是考察对时间复杂度和空间复杂度的理解和分析能力。解决这道题的思路很多。每当我们想到一种思路的时候,都要能去分析出这种思路的时间复杂度和空间复杂度各是多少,并且找到可以优化的地方。