从树的创建、遍历(包括递归、非递归)到二叉堆的构建、插入和删除最后到优先队列(含STL优先队列)
文章目录
- 树
-
- 1、二叉树(常用树结构)
-
- 1.0、什么是二叉树?(了解)
-
- 1.0.1、**特殊的二叉树**(了解)
- 1.1、二叉树的创建
-
- 1.1.1、数组创建法
-
- 1.1.1.1、为什么不建议使用数组存储
- 1.1.2、链表创建法
- 1.2、二叉树遍历
-
- 1.2.0、遍历方式(了解)
- 1.2.1、深度优先遍历
-
- 1.2.1.1、前序遍历(递归实现)
- 1.2.1.2、中序遍历(递归实现)
- 1.2.1.3、后序遍历(递归实现)
- 1.2.1.4、前序遍历(非递归实现)
- 1.2.2、广度优先遍历
-
- 1.2.2.1、层序遍历
- 1.3、完整代码:
- 2、二叉堆
-
- 2.0、什么是二叉堆?(了解)
- 2.1、构建二叉堆
- 2.2、插入节点
- 2.3、删除元素
- 2.4、完整代码:
- 3、优先队列
-
- 3.0、什么是优先队列?(了解)
- 3.1、优先队列实现
-
- 3.1.1、入队操作
- 3.1.2、出队操作
- 3.1.3、完整代码
- 3.2、STL优先队列
-
- 3.2.0、为什么要会STL优先队列?(了解)
- 3.2.1、优先队列基本操作
-
- 3.2.1.1、头文件
- 3.2.1.2、创建形式
- 3.2.1.3、优先队列操作基本函数
- 3.2.1.4、示例演示:
树
##0、什么是树?(了解)
树:树(tree)是n(n >= 0)个节点的有限集,当n=0时为空树。在任意一个非空树中满足如下特点:
1、有且仅有一个特定的称为根的节点(通俗讲,从最初的节点引出到其他节点的节点为根节点)
2、当n>1时,其余节点可分为m(m>0)个互不相交的有限集,每个集合本身也是一个树,并称为根的子树。
树的例图如下:
孩子节点:从当前节点引出来的节点(当前节点的后继节点)。
父节点:被引出来节点的节点(后继节点的前一个节点)。
叶子节点:没有“孩子”的节点(没有后继节点)
树的高度/深度:树的最大层级。(例图中的树高度为3)
n叉树:每个节点最多只能有n个孩子的树。
1、二叉树(常用树结构)
1.0、什么是二叉树?(了解)
二叉树(binary tree):树的每个节点最多有2个节点。(注意:树节点可以没有孩子节点,可以有一个孩子节点)
左孩子(left child): 二叉树一个节点左边的孩子。
右孩子(right child): 二叉树一个节点右边的孩子。
1.0.1、特殊的二叉树(了解)
满二叉树:一个二叉树的所有非叶子节点都存在左右孩子,并且所有的叶子节点都在同一级上。
如下图高度为3的满二叉树:
完全二叉树:对一个有n个节点的二叉树,按层级顺序编号,则所有节点的编号为从1到n。如果这个树所有的节点和同深度的满二叉树的编号为从1到n的节点位置相同,则这个二叉树为完全二叉树。
如下图高度为3的完全二叉树:
注意:满二叉树要求所有分支都是满的,完全二叉树只需保证最后一个节点之前的节点都齐全。
1.1、二叉树的创建
1.1.1、数组创建法
数组存储:使用数组存储时,会按照层级顺序把二叉树的节点放到数组中的对应位置,如果某一个节点的左孩子或右孩子空缺,则数组的相应位置也要空出来。
定位二叉树的父节点和孩子节点:
1、(假设父节点下标为parent)则:
左孩子下标:leftChild = 2*parent +1;
右孩子下标:rightChild = 2*parent+2;
2、(假设左孩子下标为leftChild)则:
父节点下标:parent = (leftChild - 1)/2;
3、(假设右孩子下标为rightChild)则:
父节点下标:parent = (rightChild - 2)/2;
数组存储如下:
1、二叉树形式:
2、数组存储形式:
| 0 | 1 | 2 | 3 | 4 | 6 | 7 |
|---|
1.1.1.1、为什么不建议使用数组存储
数组存储:我们从上述的数组中不难看出,在树不满足完全二叉树的形式时,会浪费掉许多空间。在实际开发中,我们很难保证我们所创建的二叉树都是完全二叉树。故多以链表的方式建立、存储。
1.1.2、链表创建法
链表存储:一个节点最多可以指向左右两个孩子节点,故二叉树的每一个节点包含三部分:
- 存储数据的data变量;
- 指向左孩子的leftChild指针;
- 指向右孩子的rightChild指针;
故结构体形式为:
typedef struct treeNode {
char data;
struct treeNode* leftChild;
struct treeNode* rightChild;
}binaryTreeNode, * binaryTreePoint;
创建步骤:(递归创建)
- 先创建头节点(头节点肯定不空)
- 创建结点的左孩子,若为空,则输入#,并返回NULL
- 接着创建右孩子,若左孩子为空,则输入#,并返回NULL,
- 递归调用3、4步骤直到创建完成。
//主要代码:
binaryTreePoint create_binary_tree() {
char ch;
binaryTreePoint treeNode;
cin >> ch;
if (ch == '#') { //表示子节点为空,停止递归调用并返回空,
return NULL;
}
else {
treeNode = (binaryTreePoint)malloc(sizeof(binaryTreeNode));
treeNode->data = ch;
cout << "请输入" << ch << "左孩子节点(输入数据(A~Z), 无则输入#) :";
treeNode->leftChild = create_binary_tree();
cout << "请输入" << ch << "右孩子节点(输入数据(A~Z), 无则输入#) :";
treeNode->rightChild = create_binary_tree();
return treeNode;
}
}
下图为创建一颗二叉树的图,其中序号表示递归创建的顺序:
1.2、二叉树遍历
1.2.0、遍历方式(了解)
a、从节点位置关系的角度考虑,二叉树遍历分为以下4种:
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
b、从更宏观的角度,二叉树的遍历分为以下2种:
- 深度优先遍历(前序遍历、中序遍历、后序遍历)
- 广度优先遍历(层序遍历)
1.2.1、深度优先遍历
1.2.1.1、前序遍历(递归实现)
前序遍历的输出顺序为:根节点、左节点、右节点(常称为:中左右)
下图为创建一颗二叉树的图,其中序号表示前序遍历输出顺序:
详细步骤如下:
- 首先输出根节点1;
- 由于根节点1存在左孩子,输出左孩子节点2;
- 由于节点2也存在左孩子,输出左孩子节点3;
- 节点3既没有左孩子,也没有右孩子,那么回到节点2,输出节点2的右孩子节点4;
- 节点4既没有左孩子,也没有右孩子,那么回到节点1,输出节点1的右孩子节点5;
- 节点5有左孩子,输出节点6;
- 由于节点6既没有左孩子,也没有右孩子,那么回到节点5;
- 由于节点5没有右孩子,那么返回到根节点(至此所有节点遍历完成)。
//主要代码:
void preorder_traversal(binaryTreePoint treeNode) {
if (treeNode == NULL) {
return;
}
else {
cout << treeNode->data;
preorder_traversal(treeNode->leftChild);
preorder_traversal(treeNode->rightChild);
}
}
1.2.1.2、中序遍历(递归实现)
中序遍历的输出顺序为:左节点、根节点、右节点(常称为:左中右)
下图为创建一颗二叉树的图,其中序号表示中序遍历输出顺序:
详细步骤如下:
- 首先访问根节点的左孩子,如果这个左孩子还拥有左孩子,则继续深入访问下一个节点,一直找到不再拥有左孩子的节点,并输出该节点。显然,第一个没有左孩子的节点为节点1;
- 依照中序遍历的次序,接下来输出节点1的父节点;
- 再输出节点2的右孩子节点3;
- 以节点2为根节点的左子树已经输出完毕,再以2为左孩子节点找其父节点,即输出其父节点4;
- 由于节点5有右孩子,故输出其左孩子节点5;
- 最后返回父节点6,输出节点6;
- 由于节点6没有右节点,故返回到根节点(至此所有节点遍历完成)。
//主要代码:
void inorder_traversal(binaryTreePoint treeNode) {
if (treeNode == NULL) {
return;
}
else {
inorder_traversal(treeNode->leftChild);
cout << treeNode->data;
inorder_traversal(treeNode->rightChild);
}
}
1.2.1.3、后序遍历(递归实现)
后序遍历的输出顺序为:左节点、右节点、根节点(常称为:左右中)
下图为创建一颗二叉树的图,其中序号表示后序遍历输出顺序:
后序遍历与前、中序遍历几乎一样,在此不再叙述。
//主要代码:
void postorder_traversal(binaryTreePoint treeNode) {
if (treeNode == NULL) {
return;
}
else {
postorder_traversal(treeNode->leftChild);
postorder_traversal(treeNode->rightChild);
cout << treeNode->data;
}
}
1.2.1.4、前序遍历(非递归实现)
前序遍历的输出顺序为:根节点、左节点、右节点(常称为:中左右)
前面介绍了递归实现的方法,其实递归操作和栈存储操作再一定程度上是相同的,下面以一个例子说明。
下图为创建一颗二叉树的图,其中序号表示前序遍历输出顺序:
具体实现步骤:
-
首先遍历根节点1,输出根节点1,并压栈;
1 -
遍历根节点1的左孩子节点2,输出节点2,并压栈;
1 2 -
遍历节点2的左孩子节点3,输出节点3,并压栈;
1 2 3 -
节点3既没有左孩子节点,也没有右孩子节点,故此时让栈顶元素3弹栈,再访问栈顶元素2,得到节点2的右孩子节点4;
1 2 -
节点2的左、右孩子已近访问过,故节点2弹栈,遍历输出节点4,节点4压栈;
1 4 -
节点4既没有左孩子节点,也没有右孩子节点,故此时让栈顶元素4弹栈,再访问栈顶元素1,得到节点1的右孩子节点5;
1 -
节点1的左、右孩子已近访问过,故节点1弹栈,遍历输出节点5,节点5压栈;
5 -
节点5没有左孩子,故访问节点5的右孩子节点6,此时节点5弹栈,节点6压栈;
6 -
节点6既没有左孩子节点,也没有右孩子节点,故此时栈空,遍历完成。
其中运用了STL栈操作,详情请看栈与队列基础操作(含STL)从函数具体实现到STL运用
//主要代码:
void preorder_stack_traversal(binaryTreePoint treeRootNode) {
stack<binaryTreePoint> s; //栈元素类型为树节点指针
binaryTreePoint treeNode = treeRootNode;
while (treeNode != NULL || !s.empty()) {
while (treeNode != NULL) { //访问节点的左孩子,并进栈
cout << treeNode->data;
s.push(treeNode);
treeNode = treeNode->leftChild;
}
if (!s.empty()) { //如果节点没有左孩子,则弹栈顶定节点,访问节点右孩子
treeNode = s.top();
s.pop();
treeNode = treeNode->rightChild;
}
}
}
1.2.2、广度优先遍历
1.2.2.1、层序遍历
层序遍历:二叉树按照从根节点到叶节点的层序关系,一层一层地横向遍历各个节点。
以下层序遍历借助队列进行操作。
下图为创建一颗二叉树的图,其中序号表示层序遍历输出顺序:
具体实现步骤:
-
根节点1入队;
1 -
节点1出队,输出节点1,并得到节点1的左孩子节点2、右孩子节点3,让节点2、3依次入队;
2 3 -
节点2出队,输出节点2,得到节点2的左孩子节点4、右孩子节点5,让节点4、5依次入队;
3 4 5 -
节点3出队,输出节点3,得到节点3的右孩子节点6,让节点6入队;
4 5 6 -
节点4出队,输出节点4,节点4没有左右孩子节点,故没有新节点入队;
5 6 -
节点5出队,输出节点5,节点5没有左右孩子节点,故没有新节点入队;
6 -
节点6出队,输出节点6,节点6没有左右孩子节点,故没有新节点入队;
-
由于此时队列为空,故所有节点遍历完成。
其中运用了STL队列操作,详情请看栈与队列基础操作(含STL)从函数具体实现到STL运用
//主要代码
void sequence_traversal(binaryTreePoint treeRootNode) {
queue<binaryTreePoint> s; 队列元素类型为树节点指针
s.push(treeRootNode);
while (!s.empty()) {
binaryTreePoint treeNode = s.front();
s.pop();
cout << treeNode->data;
if (treeNode->leftChild != NULL) {
s.push(treeNode->leftChild);
}
if (treeNode->rightChild != NULL) {
s.push(treeNode->rightChild);
}
}
}
1.3、完整代码:
代码编译器:VS2019
//主要代码 建立BinaryTree类进行封装 BinaryTree.h
#pragma once
#include //主要代码 BinaryTree.cpp
#include "BinaryTree.h"
binaryTreePoint BinaryTree::create_binary_tree() {
char ch;
binaryTreePoint treeNode;
cin >> ch;
if (ch == '#') { //表示子节点为空,停止递归调用并返回空,
return NULL;
}
else {
treeNode = (binaryTreePoint)malloc(sizeof(binaryTreeNode));
treeNode->data = ch;
cout << "请输入" << ch << "左孩子节点(输入数据(A~Z), 无则输入#) :";
treeNode->leftChild = create_binary_tree();
cout << "请输入" << ch << "右孩子节点(输入数据(A~Z), 无则输入#) :";
treeNode->rightChild = create_binary_tree();
return treeNode;
}
}
void BinaryTree::preorder_traversal(binaryTreePoint treeNode) {
if (treeNode == NULL) {
return;
}
else {
cout << treeNode->data;
preorder_traversal(treeNode->leftChild);
preorder_traversal(treeNode->rightChild);
}
}
void BinaryTree::inorder_traversal(binaryTreePoint treeNode) {
if (treeNode == NULL) {
return;
}
else {
inorder_traversal(treeNode->leftChild);
cout << treeNode->data;
inorder_traversal(treeNode->rightChild);
}
}
void BinaryTree::postorder_traversal(binaryTreePoint treeNode) {
if (treeNode == NULL) {
return;
}
else {
postorder_traversal(treeNode->leftChild);
postorder_traversal(treeNode->rightChild);
cout << treeNode->data;
}
}
void BinaryTree::preorder_stack_traversal(binaryTreePoint treeRootNode) {
stack<binaryTreePoint> s; 栈元素类型为树节点指针
binaryTreePoint treeNode = treeRootNode;
while (treeNode != NULL || !s.empty()) {
while (treeNode != NULL) { //访问节点的左孩子,并进栈
cout << treeNode->data;
s.push(treeNode);
treeNode = treeNode->leftChild;
}
if (!s.empty()) { //如果节点没有左孩子,则弹栈顶定节点,访问节点右孩子
treeNode = s.top();
s.pop();
treeNode = treeNode->rightChild;
}
}
}
void BinaryTree::sequence_traversal(binaryTreePoint treeRootNode) {
queue<binaryTreePoint> s; 队列元素类型为树节点指针
s.push(treeRootNode);
while (!s.empty()) {
binaryTreePoint treeNode = s.front();
s.pop();
cout << treeNode->data;
if (treeNode->leftChild != NULL) {
s.push(treeNode->leftChild);
}
if (treeNode->rightChild != NULL) {
s.push(treeNode->rightChild);
}
}
}
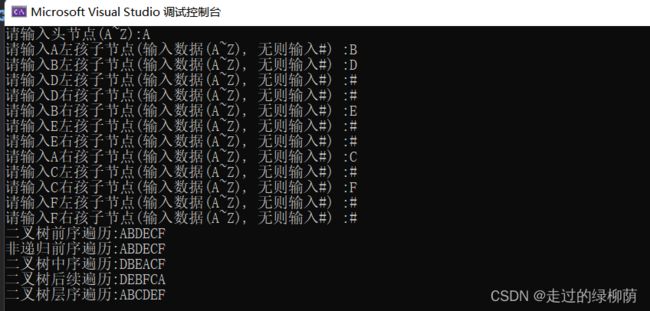
//示例代码运行 main.cpp
#include 示例截图:
2、二叉堆
2.0、什么是二叉堆?(了解)
二叉堆:二叉堆本质上是一种完全二叉树(由于是完全二叉树,利用数组存储的效率最大,事实上也是利用数组存储)。
二叉堆的分类:大根堆、小根堆。
大根堆:大根堆的任何一个父节点的值都大于或等于它左、右孩子节点的值。
下图为一个大根堆的示例:
小根堆:小根堆的任何一个父节点的值都小于或等于它左、右孩子节点的值。
下图为一个小根堆的示例:
堆顶:二叉堆的根节点。
大根堆的特点:大根堆的堆顶是整个堆中的最大元素。
小根堆的特点:小根堆的堆顶是整个堆中的最小元素。
2.1、构建二叉堆
以创建小根堆为例,进行讲解。
构建小根堆:就是把一个无序的的完全二叉树调整为二叉堆,本质上就是让所有非叶子节点依次下沉。(如果是大根堆则是让所有非叶子节点依次上浮)
下图为一个无序二叉树:
示例步骤:
-
首先,从最后一个非叶子节点开始,也就是从节点10开始。如果节点10大于它左、右孩子节点中的最小一个;则节点10”下沉“,与6进行交换;
1235107896 -
然后是节点3,如果节点3大于它左、右孩子节点中最小的一个,则节点3”下沉“,与2进行交换;
1325107896 -
然后是节点1,如果节点1大于它左、右孩子节点中最小的一个,则节点1”下沉“,但节点1小于左、右孩子节点,故不用改变;
-
然后是节点7,如果节点7大于它左、右孩子节点中最小的一个,则节点7”下沉“,与1进行交换;
7325101896 -
节点7继续比较,继续下沉,与5进行交换;
5327101896 -
经过比较后,最终每个节点都小于它的左、右孩子节点,小根堆创建完成。
//主要代码: 利用模板接受参数,使接受的参数根据有多样性。
template<class iterator>
void build_heap(iterator start, iterator end) {
int arrayLength = end - start;
for (int i = (arrayLength - 2) / 2; i >= 0; i--) { //从最后一个非叶子节点开始,依次下沉调整
down_adjustment(start, end, i, arrayLength);
}
}
template <class iterator>
void down_adjustment(iterator start, iterator end, int parentIndex, int length) {
int temp = *(start + parentIndex); //temp保存父节点值,用于最后的赋值
int childIndex = 2 * parentIndex + 1;
while (childIndex < length) {
if (childIndex + 1 < length && *(start + childIndex + 1) < *(start + childIndex)) {
childIndex++;
}
if (temp <= *(start + childIndex))
break;
*(start + parentIndex) = *(start + childIndex); //*解引用,取值
parentIndex = childIndex;
childIndex = 2 * childIndex + 1;
}
*(start + parentIndex) = temp;
}
2.2、插入节点
插入节点的位置:当二叉堆插入节点时,插入的位置时完全二叉树的最后一个位置。
下图以一个小根堆为例。(其中0为插入到末尾的元素,为节点5的左孩子)
示例步骤:
-
新插入的节点0比父节点5小,于是让新节点上浮,和父节点5交换;
left:51230678910 -
继续用节点0与父节点3作比较,因为节点3大于节点0,则让新节点继续上浮,和父节点3交换;
left:51203678910 -
继续比较,最终新节点0上浮到堆顶位置.
left:50213678910//主要代码: 利用模板接受参数,使接受的参数根据有多样性。 //插入到数组末尾的函数就省略,本质上就是再数组后再添加一个元素,模板函数为上浮元素 template <class iterator> void up_adjustment(iterator start, iterator end) { int arrayLength = end - start; int childIndex = arrayLength - 1; int parentIndex = (childIndex - 1) / 2; int temp = *(start + childIndex); while (childIndex > 0 && temp < *(start + parentIndex)) { *(start + childIndex) = *(start + parentIndex); childIndex = parentIndex; parentIndex = (parentIndex - 1) / 2; } *(start + childIndex) = temp; }
2.3、删除元素
删除元素:二叉堆删除节点的过程和插入节点的过程正好相反,所删除的元素为堆顶元素。(实际中删除元素并非真的删除,只是将其位置进行调整,并不再访问该位置)
下图以一个小根堆为例。删除节点1;
示例步骤:
-
删除节点1,把堆最后一个节点10临时补到原来的堆顶位置;
3725108left:96 -
接下来,让处于堆顶的节点10与左、右孩子节点进行比较,如果左、右孩子节点中的最小一个比节点10小,那么让节点10下沉,故与节点2进行交换;
3710528left:96 -
继续让处于节点10与左、右孩子节点进行比较,如果左、右孩子节点中的最小一个比节点10小,那么让节点10下沉,故与节点7进行交换;
3107528left:96 -
最终,二叉堆调整完成。
//主要代码:删除堆顶节点1,在此函数中,只是将堆顶节点1放在数组最后一个,并不再访问。
template<class iterator>
void delete_top(iterator start, iterator end) {
swap(*start, *(end - 1));
int arrayLength = end - start;
auto temp = *(start); //auto自动匹配数据类型
int parentIndex = 0;
int childIndex = parentIndex * 2 + 1;
while (childIndex < arrayLength - 1) {
if (childIndex + 1 < arrayLength - 1 && *(start + childIndex + 1) < *(start + childIndex)) {
childIndex++;
}
*(start + parentIndex) = *(start + childIndex);
parentIndex = childIndex;
childIndex = 2 * childIndex + 1;
}
*(start + parentIndex) = temp;
}
2.4、完整代码:
代码编译器:VS2019
/*主要代码 建立类进行封装 Heap.h 注意:写类进行封装时,不能把类写在.cpp中,模板是不能拆分的,在.h中声明,就要在.h中定义,否则会报错,在不同的编译器中,报错可能不同*/
#pragma once
#include //示例代码运行 main.cpp
#include 3、优先队列
3.0、什么是优先队列?(了解)
优先队列:优先队列不再遵循先进先出的原则,而是分为一下两种:
最大优先队列:无论入队顺序如何,都是当前最大的元素优先出队;
最小优先队列:无论入队顺序如何,都是当前最小的元素优先出队;
3.1、优先队列实现
利用线性结构实现优先队列,时间复杂度较高,因此使用二叉堆实现。
3.1.1、入队操作
以最大优先为例
入队操作:可以利用大根堆实现最大优先队列,每一次入队就是堆的插入操作(小根堆实现最小优先队列)。
下图以最大优先插入为例,插入5;
示例步骤:
-
插入新节点5;
8491210637left:5 -
新节点5上浮到合适的位置,到此入队操作结束。(提示:具体上浮操作请看前面的二叉堆)
8495210637left:1//主要代码: void push(int valua) { if (priority_queue.index >= priority_queue.arrayLength) { cout << "priority_queue full!" << endl; return; } priority_queue.array[++priority_queue.index] = valua; up_adjustment(); } void up_adjustment() { int childIndex = priority_queue.index; int parentIndex = (childIndex - 1) / 2; int temp = priority_queue.array[childIndex]; while (childIndex > 0 && temp > priority_queue.array[parentIndex]) { priority_queue.array[childIndex] = priority_queue.array[parentIndex]; childIndex = parentIndex; parentIndex = parentIndex / 2; } priority_queue.array[childIndex] = temp; }
3.1.2、出队操作
以最大优先为例
出队操作:可以利用大根堆实现最大优先队列,每一次出队就是堆的删除操作(小根堆实现最小优先队列)。
下图以最大优先删除为例,删除节点10;
示例步骤:
-
让节点10出队,把最后一个节点1替换到堆顶位置。
849521637 -
然后让节点1下沉,节点9成为新的堆顶节点。(提示:具体下沉操作请看前面的二叉堆)
846529137//主要代码: int pop() { if (priority_queue.index < 0) { cout << "priority_queue empty!" << endl; system("pause"); return 0; } int top = priority_queue.array[0]; priority_queue.array[0] = priority_queue.array[priority_queue.index--]; //让最后一个元素移动到堆顶 down_adjustment(); return top; } void down_adjustment() { int parentIndex = 0; int temp = priority_queue.array[parentIndex]; int childIndex = 1; while (childIndex <= priority_queue.index) { if (childIndex + 1 <= priority_queue.index && priority_queue.array[childIndex + 1] > priority_queue.array[childIndex]) { childIndex++; } priority_queue.array[parentIndex] = priority_queue.array[childIndex]; parentIndex = childIndex; childIndex = childIndex * 2 + 1; } priority_queue.array[parentIndex] = temp; }
3.1.3、完整代码
代码编译器:VS2019
//主要代码: 写PriorityQueue类进行封装 PriorityQueue.h
#pragma once
#include //主要代码: PriorityQueue.cpp
#include "PriorityQueue.h"
void PriorityQueue::push(int valua) {
if (priority_queue.index >= priority_queue.arrayLength) {
cout << "priority_queue full!" << endl;
return;
}
priority_queue.array[++priority_queue.index] = valua;
up_adjustment();
}
void PriorityQueue::up_adjustment() {
int childIndex = priority_queue.index;
int parentIndex = (childIndex - 1) / 2;
int temp = priority_queue.array[childIndex];
while (childIndex > 0 && temp > priority_queue.array[parentIndex]) {
priority_queue.array[childIndex] = priority_queue.array[parentIndex];
childIndex = parentIndex;
parentIndex = parentIndex / 2;
}
priority_queue.array[childIndex] = temp;
}
int PriorityQueue::pop() {
if (priority_queue.index < 0) {
cout << "priority_queue empty!" << endl;
system("pause");
return 0;
}
int top = priority_queue.array[0];
priority_queue.array[0] = priority_queue.array[priority_queue.index--]; //让最后一个元素移动到堆顶
down_adjustment();
return top;
}
void PriorityQueue::down_adjustment() {
int parentIndex = 0;
int temp = priority_queue.array[parentIndex];
int childIndex = 1;
while (childIndex <= priority_queue.index) {
if (childIndex + 1 <= priority_queue.index &&
priority_queue.array[childIndex + 1] > priority_queue.array[childIndex]) {
childIndex++;
}
priority_queue.array[parentIndex] = priority_queue.array[childIndex];
parentIndex = childIndex;
childIndex = childIndex * 2 + 1;
}
priority_queue.array[parentIndex] = temp;
}
//示例代码运行 main.cpp
#include 3.2、STL优先队列
3.2.0、为什么要会STL优先队列?(了解)
在实际开发中,优先队列的操作具有一定的通用性,且代码在本质上也相同,最多只是优先队列中存储的元素类型、大小不一。因此STL优先队列就孕育而生,其中STL优先队列具有更强的通用性。
3.2.1、优先队列基本操作
3.2.1.1、头文件
#include 3.2.1.2、创建形式
priority_queue<元素类型,容器类型,排序方式> 创建对象名
其中:1、容器类型可以用vector,deque(双向队列)等来实现,其中list不能用来实现,因为list的迭代器不是任意取iterator.
容器可以默认,如果容器默认,则排序方式也要默认(VS2019是这样的的,否则会报错)。
2、排序方式有:利用STL自带的比较大小
1)greater<元素类型> : 从小到大顺序出队,即为最小优先队列
2)less<元素类型> : 从大到小顺序出队,即为最大优先队列
3、不加排序方式默认为最大优先队列
3.2.1.3、优先队列操作基本函数
push() :添加一个元素。
pop(): 删除堆顶元素,本质上删除第一个元素,且不返回值(前提是已经形成二叉堆)。
empty():如果优先队列为空,返回true。否则,返回false。
size():返回优先队列中的元素个数
top():返回堆顶元素,本质上就是返回对一个元素(前提是已经形成二叉堆)。
3.2.1.4、示例演示:
代码编译器:VS2019
//主要代码: 写模板可接受更多不同参数类型
#include 树的学习就先告一段落,当然还有二叉搜索树(又称二叉排序树、二叉查找树),平衡二叉树,红黑树,B树B+树。我们会在后续陆续学到。希望这些分享能给你帮助。