LeetCode刷题总结C++-数组篇(上)
参考博客https://home.cnblogs.com/u/liuzhen1995/ ,题解换成C++
LeetCode刷题总结-数组篇(上)
数组是算法中最常用的一种数据结构,也是面试中最常考的考点。在LeetCode题库中,标记为数组类型的习题到目前为止,已累计到了202题。然而,这202道习题并不是每道题只标记为数组一个考点,大部分习题都有两到三个考点。比如,考查数组+哈希表、数组+动态规划+数学、数组+回溯等。
看到如此多考点标签,如果盲目地按照一个标签内部所有习题的顺序去刷题,会让人有点错乱感。对于时间比较紧凑的同学来说,题目的数量比较多,想在较短时间内刷完是一个很大的挑战。因此,本文针对时间较紧凑的同学精选一些数组类型的代表性题目,进行分类总结,希望能够起到一点帮助。
标记为数组类型的题目有200多道题,本文的重点关注那些主要考察数组的题目。对于考察点主要放在其它考点(比如:二分查找、双指针、哈希表等)上的题目,作者计划把这些题目放在后序总结篇章中。按照作者刷题的情况,在属于数组考点系列的题目中,划分为四个常考问题:子数组问题、矩阵问题、O(n)类型问题和思维转换类型问题。
- 子数组问题:就是给定一个数组,围绕该数组的子数组列出诸多难题,等待我们来解答。
- 矩阵问题:给定一个矩阵(或者称为二维数组),围绕该矩阵列出不同方式遍历矩阵中元素等难题,等待我们来解答。
- O(n)类型问题:O(n)是指时间复杂度为O(n),给定的题目题意一般很容易理解,其一般解法(俗称暴力解法,时间复杂度一般为O(n^2),甚至更高)也很简单,但是题目要求你的解法时间复杂度为O(n)。看到这些题目的某些解答后,会让我们忍不住夸赞:真乃神人、好厉害、奇异特解、巧妙、强、优雅。
- 思维转换类型问题:其解答不属于上述三种类型问题,但是解答方式有点巧妙,或者说该类型题目较为基础,很可能考察你的快速应用代码能力的题目。
本文是《LeetCode刷题总结-数组篇(上)》,总结归纳有关子数组问题的题目。本期题目数量共17题,其中难度为简单有1题,难度为中等的有12题,难度为困难的有4题。具体题目信息及解答见下文。
例1 最大子序和
题号:53,难度:简单
题目描述:
解题思路:
本题最为经典和广泛的解法是应用动态规划的思想来解答,其时间复杂度为O(n)。题目中鼓励尝试使用更为精妙的分治法求解,通过翻阅相关解答和评论发现,分治法并没有动态规划解答的优雅,其时间复杂度为O(nlogn),也并不是最优。所以,介绍一下应用动态规划解题的思路。
从数组第一个元素开始遍历,用一个一维数组存储遍历到当前元素的最大连续子数组的和。
当遍历到第i个元素时,如果前i-1和元素中连续子数组和加上第i个元素时比第i个元素的值要大,那么就更新dp[i] = dp[i-1] + nums[i],否则dp[i] = nums[i]。
具体代码:
class Solution
{
public:
int maxSubArray(vector &nums)
{
//dp[i]表示nums中以nums[i]结尾的最大子序和
vector dp(nums.size());
dp[0] = nums[0];
//类似寻找最大最小值的题目,初始值一定要定义成理论上的最小最大值
int result = nums[0];
for (int i = 1; i < nums.size(); i++)
{
dp[i] = max(dp[i - 1] + nums[i], nums[i]);
result = max(result, dp[i]);
}
return result;
}
}; 执行结果:
例2 乘积最大子序列
题号:152,难度:中等
题目描述:
解题思路:
这题其实是例1 最大子序和一个变例,由加法变换成了乘法操作(依旧是应用动态规划的思路)。此时需要做的改变是定义两个变量来存储当前子序列的乘积,一个是保存最大值,一个是保存最小值(包含负数的子序列)。
具体代码:
class Solution {
public:
int maxProduct(vector &nums) {
int maxValue = nums[0], minValue = nums[0], ans = nums[0];
int ret;
//类似寻找最大最小值的题目,初始值一定要定义成理论上的最小最大值
for (int i = 1; i < nums.size(); ++i) {
int mx = maxValue, mn = minValue;
maxValue = max(mx * nums[i], max(nums[i], mn * nums[i]));
minValue = min(mn * nums[i], min(nums[i], mx * nums[i]));
ret = max(maxValue, ret);
}
return ret;
}
}; 执行结果:
例3 子集
题号:78,难度:中等。(可参考子集II, 题号90,难度:中等)
题目描述:
解题思路:
本题考查我们应用回溯来求解所有子集的问题,在一些算法教材中最经典的问题时求解全排列的问题,解法和这道题类似。
此题需要特别注意的是,首先采用链表在递归过程中添加元素,在回溯时删除元素,能够有效提高时间效率。其次,给递归调用程序设计一个start参数,可以避免同一个元素被重复递归调用,达到了剪枝效果。
最后,在结果列表中采用重新创建一个列表存储子集的结果,是因为在递归函数中列表参数只对应一个地址,采用重新创建相当于应用了深拷贝的思想,避免了结果均为空集的情况。
具体代码:
class Solution {
public:
vector> ret;
vector> subsets(vector &nums) {
vector subRet;
dfs(nums, 0, subRet);
return ret;
}
void dfs(vector nums, int start, vector subRet) {
ret.push_back(subRet);
for (int i = start; i < nums.size(); ++i) {
subRet.push_back(nums[i]);
dfs(nums, i + 1, subRet);
subRet.pop_back();
}
}
}; 执行结果:
例4 最长连续序列
题号:128,难度:困难
题目描述:
解题思路:
采用哈希表存储数组中所有元素,然后应用哈希表查询当前元素的左右两边序列数字是否存在,查询操作的时间复杂度为O(1),所以整体的时间复杂度为O(n)。
具体代码:
class Solution {
public:
int longestConsecutive(vector nums) {
int result = 0;
set set;
for(auto n: nums)
set.insert(n);
for(auto n: nums) {
if(set.find(n) != set.end()) {
int len = 1;
int temp = n;
while(set.find(--temp) != set.end()) {
len++;
set.erase(temp);
}
temp = n;
while(set.find(++temp) != set.end()) {
len++;
set.erase(temp);
}
result = max(result, len);
}
}
return result;
}
}; 执行结果:
例5 乘积小于K的子数组
题号:713,难度:中等
题目描述:
解题思路:
本题考查应用双指针的思想,一前一后同时往后遍历。
具体代码:
class Solution {
public:
int numSubarrayProductLessThanK(vector& nums, int k) {
int result = 0, left = 0, right = 0;
int target = 1;
while(right < nums.size()) {
target *= nums[right++];
while(left < right && target >= k)
target = target / nums[left++];
result += (right - left);
}
return result;
}
}; 执行结果:
例6 和为K的子数组
题号:560,难度:中等
题目描述:
解题思路:
本题采用哈希表存储从数组第一个元素不断往后的子序列和,然后判断到当前元素的序列总和减去K的值在哈希表中有多少个,即为包含当前元素的子序列可以得到目标结果,利用前后子序列的差可以得到目标子序列和为K。
具体代码:
class Solution {
public:
int subarraySum(vector& nums, int k) {
unordered_map map;
map[0] = 1;
int count = 0, pre = 0;
for (auto& x:nums) {
pre += x;
if (map.find(pre - k) != map.end()) count += map[pre - k];
map[pre]++;
}
return count;
}
}; 执行结果:例7 可被K整除的子数组
题号:974,难度:中等
题目描述:
解题思路:
从第一个元素开始,求取连续子数组的余数(sum % k),采用Map存储每个余数的个数。
相同余数的子数组个数大于等于2时,任意选取其中两个子数组余数相减,即余数抵消,可得到一个符合题目要求的sum。(此处的个数计算方式为:n*(n-1) / 2)
但是,此处有两个需要注意的点:
(1) 如果余数为0,最终0的余数个数只有一个时(1*(1-1)/2 = 0),这样计算会漏掉(如果为多个,也会有遗漏,可以自己计算,可以自己稍微琢磨)。所以,在初始化Map时,添加以下代码:
map.insert({0, 1}); (2) 如果余数为负数,就不能执行相同余数相减抵消的操作。此时,需要做以下处理:
// sum % K 正常计算方法
((sum % K) + K) % K // 如果为负数时,需要转换为正数,这个转换原具体代码:
class Solution {
public:
int subarraysDivByK(vector& A, int K) {
unordered_map record = {{0, 1}};
int sum = 0, ans = 0;
for (int elem: A) {
sum += elem;
// 注意 C++ 取模的特殊性,当被除数为负数时取模结果为负数,需要纠正
int modulus = (sum % K + K) % K;
if (record.count(modulus)) {
ans += record[modulus];
}
++record[modulus];
}
return ans;
}
}; 执行结果:
例8 三个无重叠子数组的最大和
题号:689,难度:困难
题目描述:
解题思路:
采用动态规划求解,状态转移方程:dp[2][n] = max(dp[2][n-1], dp[1][n-k] + sumRange(n, n -k+1))。其中一维长度为3,表示三个子数组。
具体代码(代码引用自LeetCode的一个题解):
class Solution {
public:
vector maxSumOfNSubarrays(vector& nums, int k, int n) {
if (k < 1 || n * k > nums.size()) return {};
int N = nums.size();
int s = 0;
for (int i = 0; i < k; ++i) {
s += nums[i];
}
// 计算每个数的前k个数的前缀和
vector sums(N, 0);
sums[k - 1] = s;
for (int i = k; i < N; ++i) {
s += nums[i] - nums[i - k];
sums[i] = s;
}
// 动态规划
vector > dp(N, vector(n + 1, 0));
vector > path(N, vector(n + 1, 0));
dp[k - 1][1] = sums[k - 1];
path[k - 1][1] = k - 1;
for (int i = k; i < N; ++i) {
for (int j = 1; j <= n; ++j) {
dp[i][j] = dp[i - 1][j];
path[i][j] = path[i - 1][j];
if (sums[i] + dp[i - k][j - 1] > dp[i][j]) {
dp[i][j] = sums[i] + dp[i - k][j - 1];
path[i][j] = i;
}
}
}
// 路径回溯
vector res;
int ind = path[N - 1][n];
res.push_back(ind - k + 1);
for (int i = n - 1; i > 0; --i) {
ind = path[ind - k][i];
res.push_back(ind - k + 1);
}
reverse(res.begin(), res.end());
return res;
}
vector maxSumOfThreeSubarrays(vector& nums, int k) {
// 本题就是n=3的特殊情况,因此调用以下函数即可
return maxSumOfNSubarrays(nums, k, 3);
}
}; 执行结果:
例9 最长重复子数组
题号:718,难度:中等
题目描述:
解题思路:
本题既可以用哈希表来解答,也可以用动态规划的思想来解答。应用动态规划的思路解答的时间效率最高。此处介绍一下动态规划的解题思路。dp[i][j]表示A [i-1]为终点,B[j-1]为终点时两者的最长公共子数组,值为路径长度。具体更新策略见代码。
具体代码:
class Solution {
public:
int findLength(vector& A, vector& B) {
int n = A.size(), m = B.size();
vector> dp(n + 1, vector(m + 1, 0));
int ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
if (A[i - 1] == B[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
}
else {
dp[i][j] = 0;
}
ans = max(ans, dp[i][j]);
}
}
return ans;
}
}; 执行结果:
例10 匹配子序列的单词数
题号:792,难度:中等
题目描述:
解题思路:
要特别注意子序列的含义,子序列是按照从前往后的顺序任意多个元素组成的序列,其中的顺序不能更改。因此,不能应用哈希表统计字母的个数来判断是否包含某个单词。此处可采用暴力法直接匹配查找。
eg:
S = "abcde"
word = "dac"
S.find_first_of(word,1) = 2 (S当中c的位置) 即:从下标为1开始查,待查串"dac"第一个出现在S中的字符是c,返回c的下标值。
具体代码(贴一个LeetCode上评论的代码):
class Solution {
public:
int numMatchingSubseq(string S, vector& words) {
int res = 0, j;
for (int i = 0; i < words.size(); ++i) {
int position = -1;
for (j = 0; j < words[i].size(); ++j) {
position = S.find_first_of(words[i][j], position + 1); // 从下标position + 1开始遍历
if (position == -1) break; //若未找到弹出
}
if (j == words[i].size()) res ++; //表示str已全部被遍历了,则为其子串
}
return res;
}
}; 执行结果:
例11 区间子数组个数
题号:795, 难度:中等
题目描述:
解题思路:
最大元素满足大于等于L小于等于R的子数组个数 = 最大元素小于等于R的子数组个数 - 最大元素小于L的子数组个数。
具体代码:
class Solution {
public:
int numSubarrayBoundedMax(vector A, int L, int R) {
return count(A, R) - count(A, L - 1);
}
private:
int count(vector A, int bound) {
int res = 0;
int numSubarry = 0;
for (int num : A) {
if (num <= bound) {
numSubarry++;
res += numSubarry;
} else {
numSubarry = 0;
}
}
return res;
}
}; 执行结果:
例12 子数组的最小值之和
题号:907,难度:中等
题目描述:
解题思路:
参考自LeetCode的评论解答:计算每个数在子数组中最小的次数。
具体代码:
// ans:数组A[]的连续子数组最小值之和,ans=dp[0]+dp[1]+...+dp[n-1]
// dp[i]:以A[i]结尾的子数组的最小值之和,这是重点,以A[i]为结尾,意思就是 A[1,....,i],A[2,....,i]...A[i-1,i],就是线性的。
// 单调增栈st:从st[i-1]+1一直到st[i]代表一个段,且该段的最小值恰是A[st[i]]
//举个例子,对[1,3,2]来说:
//第一次1入栈,dp[0] = 1,以1结尾的;ans = dp[0] = 1;这时候只有一种情况就是{1}
//第二次3 > 1;dp[1] = dp[0] + A[1];这时候以3结尾的有两种情况{1,3},{3},所以最小值之和是 dp[1] = 1 + 3 = 4;
//第三次 2 < 3;dp[2] = {1,3,2} , {3,2},{2};然而dp[1] = {1,3},{3};所以2的出现,让{3} ——> {3,2},这里的最小值成了2;
// 所以要减去1; dp[2] = dp[1] + A[i] - 1 = 5;
//所以ans = 1 + 4 + 5 =10
class Solution {
public:
int sumSubarrayMins(vector& A) {
const int BASE = 1e9 + 7;
stack st;
int ans = 0, sum = 0; // sum:以A[i]结尾的子数组的ans,相当于dp[i]
for (int i = 0; i < A.size(); ++i) {
while (!st.empty() && A[st.top()] >= A[i]) {
int top = st.top(); st.pop();
int new_top = st.empty() ? -1 : st.top();
sum += ((A[i] - A[top]) % BASE * (top - new_top) % BASE);
}
sum = (sum + A[i]) % BASE;
ans = (ans + sum) % BASE;
st.push(i);
}
return ans % BASE;
}
}; 执行结果:
例13 子序列宽度之和
题号:891,难度:困难
题目描述:
解题思路:
具体可参考LeetCode的一篇题解。
具体代码:
class Solution {
public:
int sumSubseqWidths(vector& A) {
int MOD = (int) (1e9 + 7);
sort(A.begin(), A.end());
int n = A.size();
long res = 0;
long p = 1;
for (int i = 0; i < n; ++i) {
res = (res + (A[i] - A[n - 1 - i]) * p) % MOD;
p = (p << 1) % MOD;
}
return (int) ((res + MOD) % MOD);
}
};
执行结果:
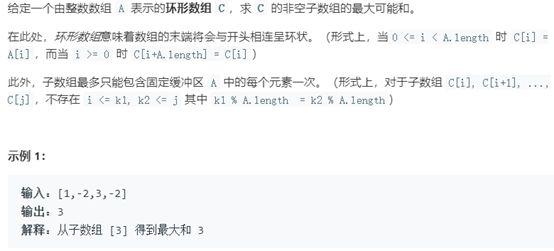
例14 环形子数组的最大和
题号:918, 难度:中等
题目描述:
解题思路:
伪代码:
#Kadane's algorithm
ans = cur = None
for x in A:
cur = x + max(cur, 0)
ans = max(ans, cur)
return ans因为题目要求有环形,所以需要定义两个变量。一个变量存储当前无环形是的连续最大子数组和,一个存储无环形连续最小子数组和。最后采用数组的总和减去最小和,和已经保存的最大和进行比较。另外,需要注意一点如果数组全部为负数时,此时直接返回子数组的最大值(因为此时,最小子数组和就是数组的和)。
具体代码:
class Solution {
public:
int maxSubarraySumCircular(vector& A) {
int maxValue = A[0];
int minValue = A[0];
int maxNew = A[0];
int minNew = A[0];
int sum = A[0];
for (int i = 1; i < A.size(); ++i) {
sum += A[i];
maxNew = max(A[i], maxNew + A[i]);
minNew = min(A[i], minNew + A[i]);
maxValue = max(maxValue, maxNew);
minValue = min(minValue, minNew);
}
if (maxValue < 0) {
return maxValue;
}
return max(maxValue, sum - minValue);
}
};
执行结果:
例15 最长湍流子数组
题号:978,难度:中等
题目描述:
解题思路:
采用连续三个位置数据是否符合湍流特征来判断,时间复杂度为O(n)。
具体代码(引用自LeetCode一个评论代码):
class Solution {
public:
int compare(int a,int b){
return (a>b)?1:(a==b)?0:-1;
}
int maxTurbulenceSize(vector& A) {
int N = A.size();
int ans = 1;
int anchor = 0;
for (int i = 1; i < N; ++i) {
int c = compare(A[i-1], A[i]);
if (i == N-1 || c * compare(A[i], A[i+1]) != -1) {
if (c != 0) ans = max(ans, i - anchor + 1);
anchor = i;
}
}
return ans;
}
};
执行结果:
例16 两个非重叠子数组的最大和
题号:1031,难度:中等
题目描述:
解题思路:
采用滑动窗口的思路来解答,对长度为L的数组,采用大小为L的滑动窗口,对于长度为M的数组采用大小为M的窗口。然后,通过两个窗口之间的距离来遍历。
考虑题意: 必然存在一条分界线把 A 拆分成两半,存在两大类情况:
长度为 L 的连续子数组在左边, 长度为 M 的连续子数组在右边
或者反过来长度为 M 的连续子数组在左边, 长度为 L 的连续子数组在右边
引入
dp[i][0]: 从 A[0]-A[i] 连续 L 长度子数组最大的元素和
dp[i][1]: 从 A[0]-A[i] 连续 M 长度子数组最大的元素和
dp[i][2]: 从 A[i]-A[A.size()-1] 连续 L 长度子数组最大的元素和
dp[i][3]: 从 A[i]-A[A.size()-1] 连续 M 长度子数组最大的元素和
某些超出范围的下标, 值设置为 0 (默认值)
代码中首先用滑动窗口计算了 dp, 然后将 dp 分成两组, 计算两大类情况下的结果,取最大值返回即可
class Solution {
public:
int maxSumTwoNoOverlap(vector& A, int L, int M) {
int len = A.size();
vector dpL(len - L + 1);
vector dpM(len - M + 1);
int maxValue = 0;
for (int i = 0; i < L; i++)
dpL[0] += A[i];
for (int i = 0; i < M; i++)
dpM[0] += A[i];
for (int i = 1; i < len - L + 1; i++)
dpL[i] = dpL[i - 1] + A[i + L - 1] - A[i - 1];
for (int i = 1; i < len - M + 1; i++)
dpM[i] = dpM[i - 1] + A[i + M - 1] - A[i - 1];
for (int i = 0; i < len - L - M + 1; i++) {
int count = len - i - L - M;
while (count >= 0) {
maxValue = max(maxValue, max(dpL[i] + dpM[i + L + count], dpM[i] + dpL[i + M + count]));
count--;
}
}
return maxValue;
}
};
执行结果:
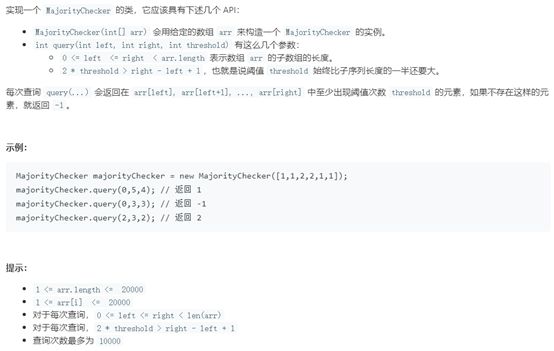
例17 子数组中占绝大多数的元素
题号:1157,难度:困难
题目描述:
解题思路:
采用哈希map来解答,一旦哈希map中目标元素值大于等于threshold,就返回目标数字,否则返回-1。
upper_bound(i) 返回的是键值为i的元素可以插入的最后一个位置(上界)
lowe_bound(i) 返回的是键值为i的元素可以插入的位置的第一个位置(下界)。
具体代码:
class MajorityChecker {
public:
unordered_map> idx;
MajorityChecker(vector& arr) {
for (auto i = 0; i < arr.size(); ++i) idx[arr[i]].push_back(i);
}
int query(int left, int right, int threshold) {
for (auto &i : idx) {
if (i.second.size() < threshold) continue;
auto it1 = lower_bound(begin(i.second), end(i.second), left);
auto it2 = upper_bound(begin(i.second), end(i.second), right);
if (it2 - it1 >= threshold) return i.first;
}
return -1;
}
}; 执行结果: