机器学习(中)-bagging套袋法原理+思路+案例
一、bagging套袋法的原理分析
Bagging(套袋法)的核心在于自助采样(bootstrap)/随机采样这一概念,即从数据集中进行有放回采样,也就是说,同样的一个样本可能被多次进行采样。
举例说明:
估计全国所有人口年龄的平均值:可在全国所有人口中随机抽取不同的集合(这些集合可能存在交集),计算每个集合的平均值,然后将所有平均值的均值作为估计值。
Bagging的基本流程:
首先随机取出一个样本放入采样集合中,再把这个样本放回初始数据集,重复K次采样,最终可获得一个大小为K的样本集合。
同样的方法,也可以采样出T个含K个样本的采样集合,然后基于每个采样集合训练出一个基学习器,再将这些基学习器进行结合。
回归问题的预测:通过预测取平均值来进行。
分类问题的预测:通过对预测取多数票预测来进行。
Bagging方法之所以有效,是因为每个模型都是在略微不同的训练数据集上拟合完成的,这又使得每个基模型之间存在略微的差异,使每个基模型拥有略微不同的训练能力。
Bagging同样是一种降低方差的技术,因此它在不剪枝决策树、神经网络等易受样本扰动的学习器上效果更加明显。在实际的使用中,加入列采样的Bagging技术对高维小样本往往有神奇的效果。
具体解释可看:https://www.cnblogs.com/pinard/p/6156009.html
二、bagging套袋法的思路
与投票法不同的是,Bagging不仅集成模型最后的预测结果,同时采用一定策略来影响基模型训练,保证基模型可以服从一定的假设。
理想状态下,各个模型之间具有较大的差异性,但在实际操作中的模型往往是同质的。
因此bagging的思路:
通过不同的采样增加模型的差异性。
三、bagging套袋法的案例分析(基于sklearn,介绍随机森林的相关理论以及实例)
Sklearn为我们提供了 BaggingRegressor 与 BaggingClassifier 两种Bagging方法的API,我们在这里通过一个完整的例子演示Bagging在分类问题上的具体应用。这里两种方法的默认基模型是树模型。
这里的树模型一般指决策树,它是一种树形结构,树的每个非叶子节点表示对样本在一个特征上的判断,节点下方的分支代表对样本的划分。决策树的建立过程是一个对数据不断划分的过程,每次划分中,首先要选择用于划分的特征,之后要确定划分的方案(类别/阈值)。我们希望通过划分,决策树的分支节点所包含的样本“纯度”尽可能地高。节点划分过程中所用的指标主要是信息增益和GINI系数。
信息增益衡量的是划分前后信息不确定性程度的减小。信息不确定程度一般使用信息熵来度量,其计算方式是:
H ( Y ) = − ∑ p i l o g p i H(Y) = -\sum{p_ilogp_i} H(Y)=−∑pilogpi
其中i表示样本的标签,p表示该类样本出现的概率。当我们对样本做出划分之后,计算样本的条件熵:
H ( Y ∣ X ) = − ∑ x ∈ X p ( X = x ) H ( Y ∣ X = x ) H(Y|X) = -\sum_{x\in X}p(X=x){H(Y|X=x)} H(Y∣X)=−x∈X∑p(X=x)H(Y∣X=x)
其中x表示用于划分的特征的取值。信息增益定义为信息熵与条件熵的差值:
I G = H ( Y ) − H ( Y ∣ X ) IG = H(Y) - H(Y|X) IG=H(Y)−H(Y∣X)
信息增益IG越大,说明使用该特征划分数据所获得的信息量变化越大,子节点的样本“纯度”越高。
同样的,我们也可以利用Gini指数来衡量数据的不纯度,计算方法如下:
G i n i = 1 − ∑ p i 2 Gini = 1 - \sum{p_i^2} Gini=1−∑pi2
当我们对样本做出划分后,计算划分后的Gini指数:
G i n i x = ∑ x ∈ X p ( X = x ) [ 1 − ∑ p i 2 ] Gini_x = \sum_{x\in X}p(X=x)[1 - \sum{p_i^2}] Ginix=x∈X∑p(X=x)[1−∑pi2]
一般来说,我们选择使得划分后Gini指数最小的特征(注意这里是直接根据Gini指数进行判断,而并非其变化量)。
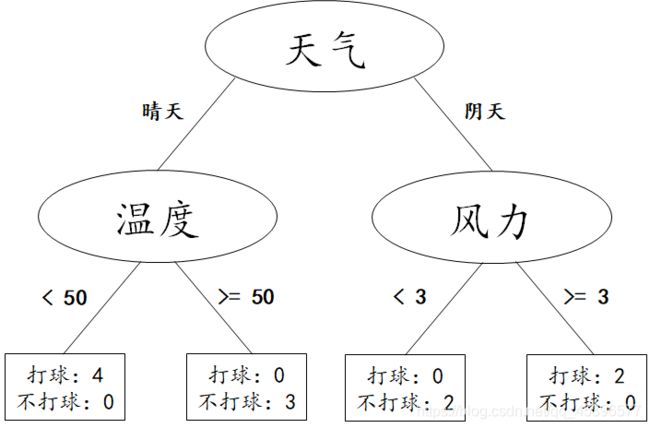
下方给出了决策树的一个例子,我们要训练一个模型,根据天气、温度和风力等级来判断是否打网球。
首先我们通过计算信息增益或Gini指数确定了首先根据天气情况对样本进行划分,之后对于每个分支,继续考虑除天气之外的其他特征,直到样本的类别被完全分开,所有特征都已使用,或达到树的最大深度为止。
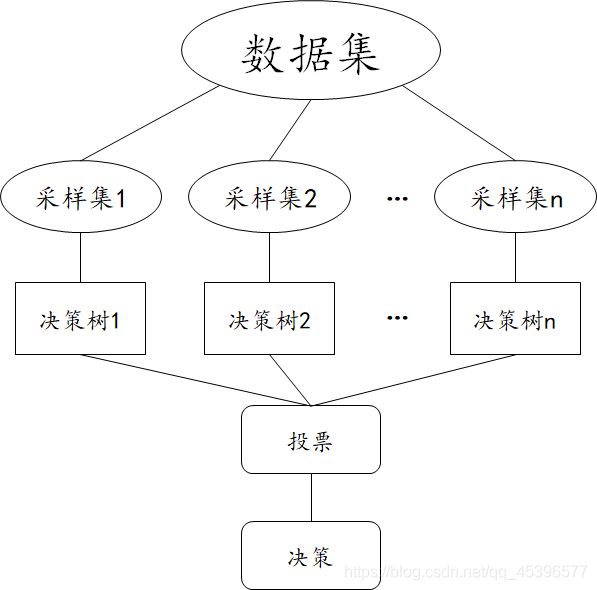
Bagging的一个典型应用是随机森林。顾名思义,“森林”是由许多“树”bagging组成的。在具体实现上,用于每个决策树训练的样本和构建决策树的特征都是通过随机采样得到的,随机森林的预测结果是多个决策树输出的组合(投票)。随机森林的示意图如下:
下面我们使用sklearn来实现基于决策树方法的bagging策略。
我们创建一个含有1000个样本20维特征的随机分类数据集:
# test classification dataset
from sklearn.datasets import make_classification
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
# summarize the dataset
print(X.shape, y.shape)
(1000, 20) (1000,)
我们将使用重复的分层k-fold交叉验证来评估该模型,一共重复3次,每次有10个fold。我们将评估该模型在所有重复交叉验证中性能的平均值和标准差。
# evaluate bagging algorithm for classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier
# define dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
# define the model
model = BaggingClassifier()
# evaluate the model
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
# report performance
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))
Accuracy: 0.864 (0.043)
最终模型的效果是Accuracy:0.864 标准差0.043