【数据结构】别跟我讲你不会冒泡排序

个人主页：Weraphael
✍作者简介：目前正在学习c++和算法
✈️专栏：数据结构
希望大家多多支持，咱一起进步！
如果文章有啥瑕疵
希望大佬指点一二
如果文章对你有帮助的话
欢迎 评论 点赞 收藏 加关注

---

一、算法思想

算法思想：两两相邻的元素进行比较，不满足要求则交换。

二、算法分析

为了加深对冒泡排序的理解，我们先模拟过程，以升序为例：

​​​​​​​​​​​​​​​​

• 第一趟排序：

第一次排序：5和9比较，满足升序，位置不变 5,9,3,6

第二次排序：9和3比较，不满足升序，位置交换，5,3,9,6

第三次排序：9和6比较，不满足升序，位置交换，5,3,6,9（此时9已经是最大的，无需参与排序）

因此，第一趟总共进行3次排序。

• 第二趟排序：

第一次排序：5和3比较，不满足升序，位置交换， 3,5,6,9

第二次排序：5和6比较，满足升序，位置不变， 3,5,6,7（此时6已经有序，无需参与排序）

因此，第二趟总共进行2次排序。

• 第三趟排序 ：

第一次排序：3和5比较，位置不变 3,5,6,7（已经有序）

因此，第三趟总共进行1次排序。

【总结】

通过以上过程的模拟，我们可以总结以下规律

1. 3个数进行冒泡排序，总趟数为3；那么n个数进行冒泡排序，总趟数为n - 1
2. 3个数进行冒泡排序，第一个数内部排序的次数为3，第二个数内部排序的次数为2…；那么n个数进行冒泡排序，内部的趟数应该是n - 1 - i

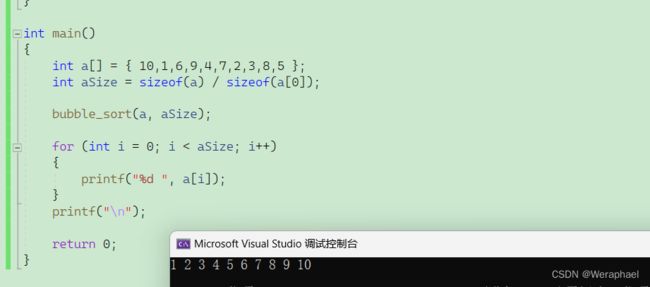
三、代码实现

#include 

void Swap(int* p1, int* p2)
{
	int t = *p1;
	*p1 = *p2;
	*p2 = t;
}

void bubble_sort(int* a, int n)
{
	// n个数有n - 1躺
	for (int i = 0; i < n - 1; i++)
	{
		// 1个数需要排n - 1 - i次
		for (int j = 0; j < n - 1 - i; j++)
		{
			// 两两比较，不满足条件交换
			if (a[j + 1] < a[j])
			{
				Swap(&a[j + 1], &a[j]);
			}
		}
	}
}

int main()
{
	int a[] = { 10,1,6,9,4,7,2,3,8,5 };
	int aSize = sizeof(a) / sizeof(a[0]);

	bubble_sort(a, aSize);

	for (int i = 0; i < aSize; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");

	return 0;
}

【程序结果】

四、优化版思路 + 代码实现

思路：优化版是对序列进行了特判，如果某一趟遍历数组发现内部根本没有进行交换，就代表其有序

【代码实现】

这里我就不直接给出完整的代码，因为我发现有很多人搞不定边界问题，这次我就带领大家来一起分析

想搞定任何一个排序问题，首先你就必须要先写出单躺

假设i指向序列下标为1的位置，那我们就想i最多能到哪个地方(边界)。因为冒泡排序需要进行两两比较，那么i就一定不能等于序列长度n。因此i < n。以下就是单趟代码

void bubble_sort(int* a, int n)
{
	// 单趟
	for (int i = 1; i < n; i++)
	{
		if (a[i - 1] > a[i])
		{
			Swap(&a[i - 1], &a[i]);
		}
	}
}

那接下来想：由于单趟排完之后，序列的最后一个数已经是有序的了，那么循环的判断条件就不能一直是i < n，必须要有一个变量来控制。而一开始我我们已经分析过了，n个数的冒泡排序的总趟数是n - 1

void bubble_sort(int* a, int n)
{
	for (int j = 0; j < n - 1; j++)
	{
		for (int i = 1; i < n - j; i++)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
			}
		}
	}
}

最后再根据优化思路，因此优化后的完整代码 如下：

【完整代码】

#include 
#include 

void Swap(int* p1, int* p2)
{
	int t = *p1;
	*p1 = *p2;
	*p2 = t;
}

void bubble_sort(int* a, int n)
{
	for (int j = 0; j < n - 1; j++)
	{
		bool flag = true;
		for (int i = 1; i < n - j; i++)
		{
			if (a[i - 1] > a[i])
			{
				Swap(&a[i - 1], &a[i]);
				flag = false;
			}
		}
		// 如果一趟排序后，没有发生交换->flag没有发生改变
		// 那么序列一定有序
		if (flag)
			break;
	}
}

int main()
{
	int a[] = { 10,1,6,9,4,7,2,3,8,5 };
	int aSize = sizeof(a) / sizeof(a[0]);

	bubble_sort(a, aSize);

	for (int i = 0; i < aSize; i++)
	{
		printf("%d ", a[i]);
	}
	printf("\n");

	return 0;
}

五、性能分析

• 时间复杂度

① 未优化版的时间复杂度最好和最坏的情况：不管怎样每一个数都要进行两两比较，因此时间复杂度为：O(N²）
② 而优化版最好的情况就是第一趟下来，没有发生交换，因此最好的时间复杂度是O(N)，最坏的情况还是O(N²）

综上：冒泡排序的时间复杂度是O(N²）

• 空间复杂度：O(1)
• 稳定性：稳定