LC-1334. 阈值距离内邻居最少的城（Floyd算法，记忆化搜索 ==＞ 动态规划(0x3f)）

1334. 阈值距离内邻居最少的城市

中等

有 n 个城市，按从 0 到 n-1 编号。给你一个边数组 edges，其中 edges[i] = [fromi, toi, weighti] 代表 fromi 和 toi 两个城市之间的双向加权边，距离阈值是一个整数 distanceThreshold。

返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold 的城市。如果有多个这样的城市，则返回编号最大的城市。

注意，连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。

示例 1：

输入：n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
输出：3
解释：城市分布图如上。
每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是：
城市 0 -> [城市 1, 城市 2] 
城市 1 -> [城市 0, 城市 2, 城市 3] 
城市 2 -> [城市 0, 城市 1, 城市 3] 
城市 3 -> [城市 1, 城市 2] 
城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市，但是我们必须返回城市 3，因为它的编号最大。

示例 2：

输入：n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
输出：0
解释：城市分布图如上。 
每个城市阈值距离 distanceThreshold = 2 内的邻居城市分别是：
城市 0 -> [城市 1] 
城市 1 -> [城市 0, 城市 4] 
城市 2 -> [城市 3, 城市 4] 
城市 3 -> [城市 2, 城市 4]
城市 4 -> [城市 1, 城市 2, 城市 3] 
城市 0 在阈值距离 2 以内只有 1 个邻居城市。

提示：

• 2 <= n <= 100
• 1 <= edges.length <= n * (n - 1) / 2
• edges[i].length == 3
• 0 <= fromi < toi < n
• 1 <= weighti, distanceThreshold <= 10^4
• 所有 (fromi, toi) 都是不同的。

记忆化搜索（0x3f）

https://leetcode.cn/problems/find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance/solutions/2525946/dai-ni-fa-ming-floyd-suan-fa-cong-ji-yi-m8s51/?envType=daily-question&envId=2023-11-14

题意解读：对于城市i，求出i到其余城市的最短路长度，统计有多少个最短路长度 <= distanceThreshold

启发思考：

class Solution {
    public int findTheCity(int n, int[][] edges, int distanceThreshold) {
        int[][] w = new int[n][n];
        for(int[] row : w)
            Arrays.fill(row, Integer.MAX_VALUE / 2);
        for(int[] e : edges){
            int x = e[0], y = e[1], wt = e[2];
            w[x][y] = w[y][x] = wt;
        }
        int[][][] memo = new int[n][n][n];

        int ans = 0;
        int minCnt = n;
        for(int i = 0; i < n; i++){
            int cnt = 0;
            for(int j = 0; j < n; j++){
                if(j != i && dfs(n-1, i, j, memo, w) <= distanceThreshold){
                    cnt++;
                }
            }
            if(cnt <= minCnt){ // 相等时取最大的 i
                minCnt = cnt;
                ans = i;
            }
        }
        return ans;
    }

    /**
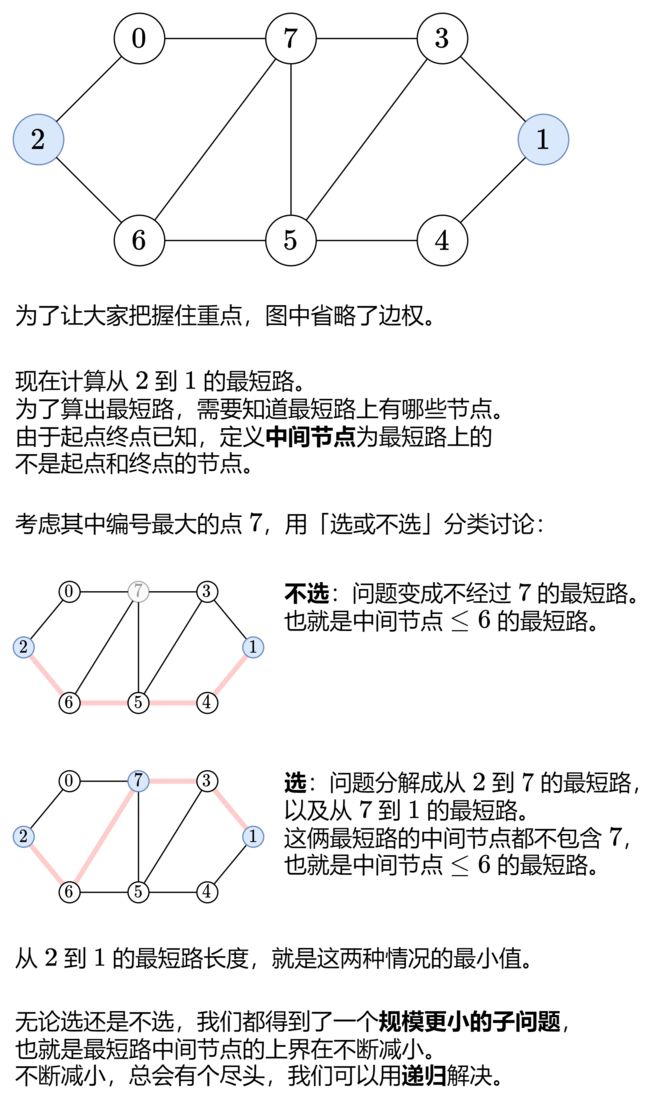
    定义 dfs(k, i, j) 表示从 i 到 j 的最短路长度，并且这条最短路的中间节点编号都 <= k
                    注意中间结点不包含 i 和 j
    转移 
    不选 k， 那么中间结点的编号都 <= k-1，即 dfs(k, i, j) = dfs(k-1, i, j)
    选 k， 那么问题分解成从 i 到 k 的最短路，以及从 k 到 j 的最短路，由于这两条最短路的中间结点不包含k
            所有中间结点标号都 <= k-1，即 dfs(k, i, j) = dfs(k-1, i, k) + dfs(k-1, k, k)
        这两种情况取最小值
    递归边界 dfs(-1, i, j) = w[i][j], k=-1 表示 i 和 j 之间没有任何中间节点，最短路长度只能是i和j的边权
                                        如果没有连接 i 和 j 的边，那么 w[i][j] = ∞
    递归入口 dfs(n-1, i, j) 表示 i 到 j 的最短路长度，k=n-1 是因为本题结点编号 0 到 n-1
     */
    public int dfs(int k, int i, int j, int[][][] memo, int[][] w){
        if(k < 0)
            return w[i][j];
        if(memo[k][i][j] != 0)
            return memo[k][i][j];
        return memo[k][i][j] = Math.min(dfs(k-1, i, j, memo, w), 
                                dfs(k-1, i, k, memo, w) + dfs(k-1, k, j, memo, w));
    }
}

转递推

问: 为什么一定要在最外层枚举 k ?

答: 仔细看上面的状态转移方程，要正确地算出 f[k+1][i][j] ，必须先把 f[k][i][j]、f[k][i][k]和 f[k][k][j] 算出来。由于我们不知道 k 和i,j的大小关系，只有把 k 放在最外层枚举，才能保证先把 f[k][i][j]、f[k][i][k]和 f[k][k][j] 算出来。顺带一提，对于 i 和 j 来说，由于在计算 f[k+1][i][j] 的时候，f[k][.][.] 已经全部计算完毕，所以 i 和 j 按照正序/逆序枚举都可以。

class Solution {
    /**
    第 0 位表示 k=-1 的情况
    f[k+1][i][j] = Math.min(f[k][i][j], f[k][i][k] + f[k][k][j])
    初始化 f[0][i][j] = w[i][j]
     */
    public int findTheCity(int n, int[][] edges, int distanceThreshold) {
        int[][] w = new int[n][n];
        for(int[] row : w)
            Arrays.fill(row, Integer.MAX_VALUE / 2);
        for(int[] e : edges){
            int x = e[0], y = e[1], wt = e[2];
            w[x][y] = w[y][x] = wt;
        }
        int[][][] f = new int[n+1][n][n];
        f[0] = w;
        for(int k = 0; k < n; k++){
            for(int i = 0; i < n; i++){
                for(int j = 0; j < n; j++){
                    f[k+1][i][j] = Math.min(f[k][i][j], f[k][i][k] + f[k][k][j]);
                }
            }
        }
        int ans = 0;
        int minCnt = n;
        for(int i = 0; i < n; i++){
            int cnt = 0;
            for(int j = 0; j < n; j++){
                if(j != i && f[n][i][j] <= distanceThreshold){
                    cnt++;
                }
            }
            if(cnt <= minCnt){ // 相等时取最大的 i
                minCnt = cnt;
                ans = i;
            }
        }
        return ans;

    }
}

状态优化

class Solution {
    /**
    在计算f[k+1]的时候，只会用到f[k]
    f[k+1][i][k] 表示 从 i 到 k 的最短路长度，且这条最短路的中间节点编号都 <= k
            由于终点是 k，那么中间节点必然不包含 k，所以中间节点编号都 <= k-1
    ==> f[k+1][i][k] = f[k][i][k]
    同理，f[k+1][k][j] = f[k][k][j]
     */
    public int findTheCity(int n, int[][] edges, int distanceThreshold) {
        int[][] w = new int[n][n];
        for(int[] row : w)
            Arrays.fill(row, Integer.MAX_VALUE / 2);
        for(int[] e : edges){
            int x = e[0], y = e[1], wt = e[2];
            w[x][y] = w[y][x] = wt;
        }
        int[][] f = new int[n][n];
        f = w;
        for(int k = 0; k < n; k++){
            for(int i = 0; i < n; i++){
                for(int j = 0; j < n; j++){
                    f[i][j] = Math.min(f[i][j], f[i][k] + f[k][j]);
                }
            }
        }
        int ans = 0;
        int minCnt = n;
        for(int i = 0; i < n; i++){
            int cnt = 0;
            for(int j = 0; j < n; j++){
                if(j != i && f[i][j] <= distanceThreshold){
                    cnt++;
                }
            }
            if(cnt <= minCnt){ // 相等时取最大的 i
                minCnt = cnt;
                ans = i;
            }
        }
        return ans;

    }
}