海亮DAY8 关于Tarjan算法用于割点割边相关感受

Tarjan

简介

Tarjan算法在求割点，割边，连通分量方面及其高效，在军事，交通，设计等方面有重要作用。

由于Tarjan算法思想并不难懂，在此不放上Tarjan算法的具体介绍。

[Usaco2006 Jan] Redundant Paths 分离的路径

传送门
两个点有两条不同的路径，显然这两点组成了一个环。那么我们思考环的特性。显然环是没有割边与割点的。由此想到Tarjan算法求双联通分量。
由严格证明（显然证明法）可知：
答案是度为1的边双连通分量的一半

• 为什么
  显见对一个无向图做边双连通分量缩点由双连通分量可知，缩点后不会形成环，即树。
  而我们也可以证明，一个图任意两点存在两条以上的路径是图无割边的充分必要条件。
  那么问题就转化为：
  对于一个树，增加一些边，求使其不存在割边的最小边数

现在我们的方向就比较明确了。

根据最开始的讨论：两点有两条路径，即成环。
所以只需要将加的边生成环即可。
再根据贪心的思想，每一个环囊括尽可能多的节点。
例如：
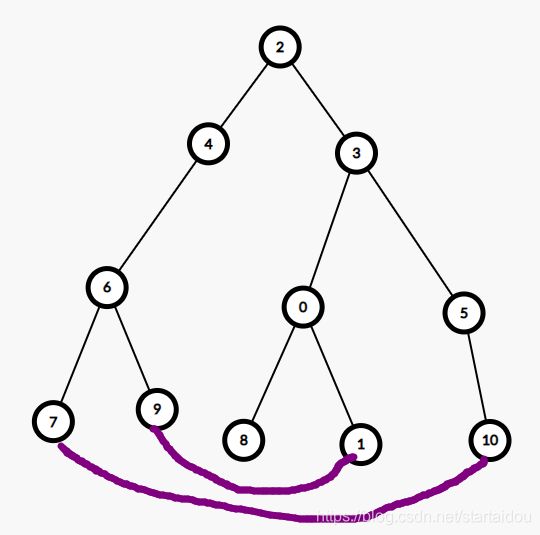那么8节点呢？？
随便连一个就好了。
这是代码。

#include
#include
#include
#include
using namespace std;
const int maxn=5010;
const int maxm=20010;
int n,m,u[maxn],v[maxn],x,y,len=0,head[maxn],ne[maxm],p[maxm],id=0,dfn[maxn],low[maxn],bcc[maxn],deg[maxn],ans=0,anss=0;
bool vis[maxm];
stack<int> st;
inline void adde(int x,int y)
{
    ne[++len]=head[x];
    head[x]=len;
    p[len]=y;
}
void dfs(int cur)
{
	++id;
    dfn[cur]=id;
	low[cur]=id;
    int j=head[cur];
    while(j)
    {
		if(vis[j])
    	{
    	    int i=p[j];
    	    if(dfn[i]) low[cur]=min(low[cur],dfn[i]);
    	    else
    	    {
    	        st.push(i);
    	        vis[j]=vis[(j&1) ? j+1 : j-1]=false;
    	        dfs(i);
    	        vis[j]=vis[(j&1) ? j+1 : j-1]=true;
    	        low[cur]=min(low[cur],low[i]);
    	    }
    	}
    j=ne[j];
	}
    if(dfn[cur]==low[cur])
    {
        ++ans;
        while(!st.empty())
        {
            bcc[st.top()]=ans;
            if(st.top()==cur){st.pop();break;} 
            st.pop();
        }
    } 
}
int main()
{
    memset(head,0,sizeof(head));
    memset(dfn,0,sizeof(dfn));
    memset(low,0,sizeof(low));
    memset(deg,0,sizeof(deg));
    memset(bcc,0,sizeof(bcc));
    memset(vis,true,sizeof(vis));
    scanf("%d%d",&n,&m);
    int i=1;
    while(i<=m)
	{
		scanf("%d%d",u+i,v+i);
		adde(u[i],v[i]);
		adde(v[i],u[i]);
		++i;
	}
	i=1;
    while(i<=n)
	{
		if(!dfn[i])
		{
			ans=0;
			st.push(i);
			dfs(i);
		}
		++i;
	}
	i=1;
    while(i<=m)
	{
		if(bcc[u[i]]!=bcc[v[i]])
		{
			++deg[bcc[u[i]]];
			++deg[bcc[v[i]]];
		}
		++i;
	}
	i=1;
	while(i<=n)
	{
		if(deg[i]==1) ++anss;
		++i;
	}
    printf("%d\n",(anss+1)/2);
    return 0;
}

逃不掉的路

找不到链接，粘原文。

现代社会，路是必不可少的。任意两个城镇都有路相连，而且往往不止一条。但有些路连年被各种XXOO，走着很不爽。按理说条条大路通罗马，大不了绕行其他路呗——可小撸却发现：从a城到b城不管怎么走，总有一些逃不掉的必经之路。

他想请你计算一下，a到b的所有路径中，有几条路是逃不掉的？

输入格式

第一行是n和m，用空格隔开。

接下来m行，每行两个整数x和y，用空格隔开，表示x城和y城之间有一条长为1的双向路。

第m+2行是q。接下来q行，每行两个整数a和b，用空格隔开，表示一次询问。

输出格式

对于每次询问，输出一个正整数，表示a城到b城必须经过几条路。
样例输入

5 5
1 2
1 3
2 4
3 4
4 5
2
1 4
2 5

样例输出

0
1

这显然是模板题。根据上题的思想，缩点成树。
我们又知道割边一定要经过。
那就缩点后lca求一下点距。AC

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int maxn=100010;
const int maxm=400010;
int n,m,u[maxm],v[maxm],x,y,len=0,head[maxn],ne[maxm],p[maxm],id=0,dfn[maxn],low[maxn],bcc[maxn],ans=0,anss=0,pp[maxn][22],dee[maxn],q=0;
bool vis[maxm];
stack<int> st;
inline void adde(int x,int y)
{
    ne[++len]=head[x];
    head[x]=len;
    p[len]=y;
}
void dfs(int cur)
{
	++id;
    dfn[cur]=id;
	low[cur]=id;
    int j=head[cur];
    while(j)
    {
		if(vis[j])
    	{
    	    int i=p[j];
    	    if(dfn[i]) low[cur]=min(low[cur],dfn[i]);
    	    else
    	    {
    	        st.push(i);
    	        vis[j]=vis[(j&1) ? j+1 : j-1]=false;
    	        dfs(i);
    	        vis[j]=vis[(j&1) ? j+1 : j-1]=true;
    	        low[cur]=min(low[cur],low[i]);
    	    }
    	}
    j=ne[j];
	}
    if(dfn[cur]==low[cur])
    {
        ++ans;
        while(!st.empty())
        {
            bcc[st.top()]=ans;
            if(st.top()==cur){st.pop();break;} 
            st.pop();
        }
    } 
}
void dfss(int x,int f)
{
	dee[x]=dee[f]+1;
	pp[x][0]=f;
	int i=1;
	while(i<=20)
	{
		pp[x][i]=pp[pp[x][i-1]][i-1];
		++i;
	}
	i=head[x];
	while(i)
	{
		int y=p[i];
		if(y!=f) dfss(y,x);
		i=ne[i];
	}
	return ;
}
int lca(int x,int y)
{
	if(dee[y]>dee[x]) swap(x,y);
	int i=20;
	while(i>=0)
	{
		if(dee[pp[x][i]]>=dee[y]) x=pp[x][i];
		if(dee[x]==dee[y]) break;
		--i;
	}
	if(x==y) return x;
	i=20;
	while(i>=0)
	{
		if(pp[x][i]!=pp[y][i])
		{
			x=pp[x][i];
			y=pp[y][i];
		}
		--i;
	}
	return pp[x][0];
}
int main()
{
    memset(head,0,sizeof(head));
    memset(dfn,0,sizeof(dfn));
    memset(low,0,sizeof(low));
    memset(bcc,0,sizeof(bcc));
    memset(dee,0,sizeof(dee));
    memset(vis,0,sizeof(vis));
    memset(pp,0,sizeof(pp));
    memset(vis,true,sizeof(vis));
    scanf("%d%d",&n,&m);
    int i=1;
    while(i<=m)
	{
		scanf("%d%d",u+i,v+i);
		adde(u[i],v[i]);
		adde(v[i],u[i]);
		++i;
	}
	i=1;
    while(i<=n)
	{
		if(!dfn[i])
		{
			ans=0;
			st.push(i);
			dfs(i);
		}
		++i;
	}
	memset(head,0,sizeof(head));
	memset(ne,0,sizeof(ne));
	memset(p,0,sizeof(p));
	len=0;
	i=1;
	while(i<=m)
	{
		if(bcc[u[i]]!=bcc[v[i]])
		{
			adde(bcc[u[i]],bcc[v[i]]);
			adde(bcc[v[i]],bcc[u[i]]);
		}
		++i;
	}
	dee[0]=0;
	dfss(1,0);
	scanf("%d",&q);
	i=1;
	int a,b;
	while(i<=q)
	{
		scanf("%d%d",&a,&b);
		int lc=lca(bcc[a],bcc[b]);
		printf("%d\n",dee[bcc[a]]+dee[bcc[b]]-2*dee[lc]);
		++i;
	}
    return 0;
}

【hdoj3394】railway

传送门
简单环，多余边。我们可以确定分别对应的点双算法和Tarjan求割边（桥）。
割边可以用模板，简单环呢？
用点双就行了。
将图分成多个双连通分量，判断每个连通分量的边是否大于点数就行了（为什么？）。如果是，就将答案加上边数。
AC代码

AC

???

AC!!

??

A…

但在此之前，我在hdoj上ac过了。
经过多次造数据，我终于发现是重边的问题。
怎么办呢？
在Tarjan算法里判断一个边会不会经过两次就行了。
经过两次就让它通过就行。
最终代码。

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
int n,len=0,m,hea[10010],dfn[10010],low[10010],id=0,num=0,cnt=0,ans=0,lin=0;
bool vis[10010];
bool ins[10010];
int sk[10010],top=0;
int gro=0,root=0,rs=0,si=0;
int vss[10010];
int blo[10010];
struct nobe
{
	int ne,to,id;
}e[200010];
bool mmp(nobe x,nobe y)
{
	return (x.ne<y.ne)||((x.ne==y.ne)&&(x.to<y.to));
}
inline int read()
{
    char c;
	int r;
    while(c=getchar()){if((c>='0')&&(c<='9')){r=c^0x30;break;}}
    while(isdigit(c=getchar())) r=(r<<3)+(r<<1)+(c^0x30);
    return r;
}
inline void adde(int u,int v,int id)
{
	e[++len].to=v;
	e[len].ne=hea[u];
	e[len].id=id;
	hea[u]=len;
}
void dfss(int now,int fa)
{
    ++id;
    dfn[now]=id;
    low[now]=id;
    int i=hea[now];
    bool fl=0;
    while(i)
    {
    	if((e[i].to==fa)&&(!fl))
    	{
    		fl=true;
    		i=e[i].ne;
    		continue ;
		}
        if(dfn[e[i].to]==0)
        dfss(e[i].to,now);
		low[now]=min(low[now],low[e[i].to]);
        if(low[e[i].to]>dfn[now]) ++ans;
        i=e[i].ne;
    }
}
void ck()
{
    int num=0;
    int t=1,i;
    while(t<=blo[0])
    {
    	i=hea[blo[t]];
        while(i)
        {
            int j=e[i].to;
            if(ins[j]) ++num;
            i=e[i].ne;
        }
        ++t;
    }
    num/=2;
    if(blo[0]<num) ans+=num;
}
 
void tarjan(int u,int fa)
{
    int v;
    ++id;
    low[u]=id;
	dfn[u]=id;
    sk[top++]=u;
 	int i=hea[u];
    while(i)
    {
        int v=e[i].to;
        if(!dfn[v])
        {
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u])
            {
                memset(ins,false,sizeof(ins));
                blo[0]=0;
                do
                {
                    blo[++blo[0]]=sk[--top];
                    ins[sk[top]]=true;
                }while(sk[top]!=v);
                blo[++blo[0]]=u;
                ins[u]=true;
                ck();
            }
        }
        else low[u]=min(low[u],dfn[v]);
        i=e[i].ne;
    }
}
int main()
{
freopen("way.in","r",stdin);
freopen("way.out","w",stdout);
	while(1)
	{
	n=0;
	id=0;
	rs=0;
	len=0; 
	num=0;
	cnt=0;
	gro=0;
	ans=0;
	lin=0;
	top=0;
	memset(dfn,0,sizeof(dfn));
	memset(low,0,sizeof(low));
	memset(vis,0,sizeof(vis));
	memset(hea,0,sizeof(hea));
	memset(vss,0,sizeof(vss));
	++si;
	int i=1,a,b;
	n=read();
	m=read();
	if((m==0)&&(n==0)) return 0;
	while(i<=m)
	{
		a=read();
		b=read();
		adde(a,b,i);
		adde(b,a,i);
		++i;
	}
	i=0;
	while(i<n)
	{
		if(!dfn[i]) dfss(i,-1);
		++i;
	}
	memset(dfn,0,sizeof(dfn));
	id=0;
	printf("%d ",ans);
	ans=0;
	i=0;
	while(i<n)
	{
		if(!dfn[i]) tarjan(i,i);
		++i;
	}
	printf("%d\n",ans);
	}
	return 0;
}

【hnoi2012_bzoj2730】矿场搭建

传送门
显然是数学题。
现在考虑各种情况。

• 一个联通子图如果没有割点，那只建一个的话，显然塌了所有人都出不去。所以最少两个。方案数为点数*（点数-1）/2。
• 若有一个割点，任何点塌，都不影响图的连通。即使避难所塌了，你也可以通过割点逃到其他子图。所以最少一个。方案数为非割点。
• 若此图割点大于等于2，怎么塌你都能逃出去。

加上乘法原理，加法原理，此题A了。

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
int n,len=0,m,hea[100010],dfn[100010],low[100010],id=0,num=0,cnt=0,gro=0,root=0,rs=0,si=0;
bool vis[100010];
int vss[100010];
unsigned long long ans=0,anss=0;
struct nobe
{
	int ne,to;
}e[600010];
inline int read()
{
    char c;
	int r;
    while(c=getchar()){if((c>='0')&&(c<='9')){r=c^0x30;break;}}
    while(isdigit(c=getchar())) r=(r<<3)+(r<<1)+(c^0x30);
    return r;
}
inline void adde(int u,int v)
{
	e[++len].to=v;
	e[len].ne=hea[u];
	hea[u]=len;
}
void tarjan(int u,int f)
{
	++id;
    int v;
    dfn[u]=id;
	low[u]=id;
	int i=hea[u];
    while(i)
    {
        v=e[i].to;
        if(!dfn[v])
        {
            tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u])
            {
                if(u!=root) vis[u]=true;
                else ++rs;
            }
        }
        else if(v!=f) low[u]=min(low[u],dfn[v]);
        i=e[i].ne;
    }
}
void dfs(int u)
{
	int v;
    vss[u]=gro;
    ++num;
	int i=hea[u];
    while(i)
    {
        v=e[i].to;
        if((vis[v])&&(vss[v]!=gro)) 
        {
            ++cnt;
            vss[v]=gro;
        }
        if(!vss[v]) dfs(v);
        i=e[i].ne;
    }
}
int main()
{
	while(1)
	{
	n=0;
	id=0;
	rs=0;
	len=0;
	ans=0;
	num=0;
	cnt=0;
	ans=0;
	gro=0;
	anss=1;
	memset(dfn,0,sizeof(dfn));
	memset(low,0,sizeof(low));
	memset(vis,0,sizeof(vis));
	memset(hea,0,sizeof(hea));
	memset(vss,0,sizeof(vss));
	++si;
	int i=1,a,b;
	m=read();
	if(m==0) return 0;
	while(i<=m)
	{
		a=read();
		b=read();
		adde(a,b);
		adde(b,a);
		n=max(n,max(a,b));
		++i;
	}
	i=1;
	while(i<=n)
	{
		if(!dfn[i])
		{
			rs=0;
			root=i;
			tarjan(i,i);
			if(rs>=2) vis[root]=true;
		}
		++i;
	}
	i=1;
	while(i<=n)
	{
		if((!vss[i])&&(!vis[i]))
		{
			++gro;
			num=0;
			cnt=0;
			dfs(i);
			if(cnt==0)
			{
				ans+=2;
				anss*=((num-1)*num)/2;
			}
			else if(cnt==1)
			{
				ans+=1;
				anss*=num;
			}
		}
		++i;
	}
	printf("Case %d: %lld %lld\n",si,ans,anss);
	}
	return 0;
 } 

以上