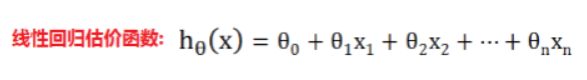python手写函数与调用库分别实现逻辑回归与线性回归

逻辑回归

使用uci数据集中的data_banknote_authentication数据进行逻辑回归。
数据集：

代价cost:

最终目标是要求出使得 J(theta)最小时theta的值。采取的方法均为类似梯度下降法的方法。

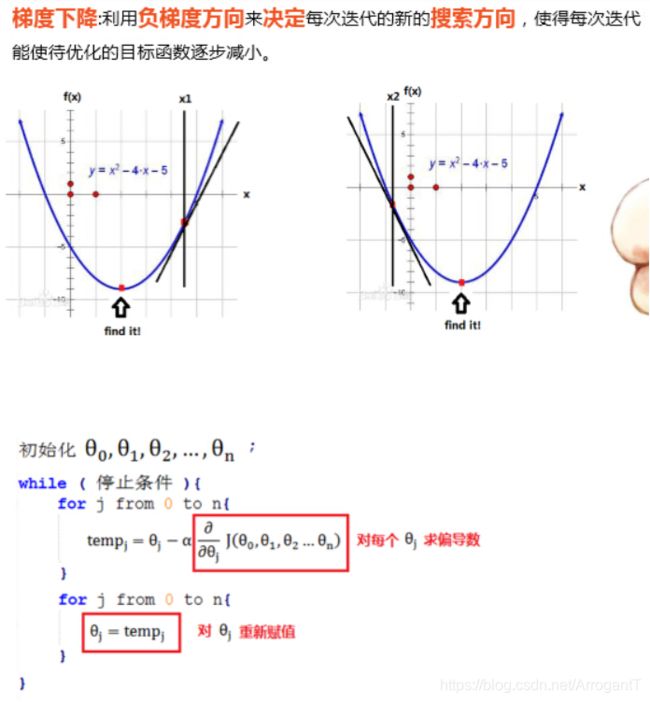
不调库代码实现：

import pandas as pd

# 加载数据集
data= pd.read_csv('D:/Desktop/data_banknote_authentication.txt',header=None)
print(data.head())

X = data[[0,1,2,3]]  # 取前四个作为特征
y = data[[4]]

import math

MAX_FEATURE_DIMENSION = 1024
MAX_SAMPLE_NUMBER = 1024
MAX_ITERATE_NUMBER = 1024

##估价函数
def sigmoid(z):
    return(1 / (1.0 + math.exp(-z)))

def hypothesis(x, theta, feature_number):
    h = 0.0
    for i in range(feature_number+1):
        h += x[i] * theta[i]
    return(sigmoid(h))

##计算偏导数
def compute_gradient(x, y, theta, feature_number, feature_pos, sample_number):
    sum = 0.0
    for i in range(sample_number):
        h = hypothesis(x[i], theta, feature_number)
        sum += (h - y[i]) * x[i][feature_pos]
    return(sum / sample_number)


##代价
def compute_cost(x, y, theta, feature_number, sample_number):
    sum = 0.0
    for i in range(sample_number):
        h = hypothesis(x[i], theta, feature_number)
        sum += -y[i] * math.log(h) - (1 - y[i]) * math.log(1 - h)
    return(sum / sample_number)

##梯度下降
def gradient_descent(x, y, theta, feature_number, sample_number, alpha, count):
    for i in range(count):
        tmp = []
        for j in range(MAX_FEATURE_DIMENSION):
            tmp.append(0)
        for j in range(feature_number + 1):
            tmp[j] = theta[j] - alpha * compute_gradient(x, y ,theta, feature_number, j, sample_number)
        for j in range(feature_number + 1):
            theta[j] = tmp[j]
        print(compute_cost(x, y, theta, feature_number, sample_number))
        
if __name__ == '__main__':
    sample_number = X.shape[0]
    count = 30000 # 迭代次数
    feature_number = 3
    alpha = 0.002 # 步长

    theta = []
    for i in range(MAX_FEATURE_DIMENSION):
        theta.append(0)

    gradient_descent(X.values.tolist(), y[4].tolist(), theta, feature_number, sample_number, alpha, count)

    theta1 = []
    for i in range(feature_number+1):
        theta1.append(theta[i])
    print("cost收敛时的theta值：",theta1)

代码实现（调用sklearn）：

import pandas as pd

# 加载数据集
data= pd.read_csv('D:/Desktop/data_banknote_authentication.txt',header=None)
print(data.head())

from sklearn.model_selection import train_test_split
X = data[[0,1,2,3]]  # 取前四个作为特征
y = data[[4]]
X_train, X_test, y_train, y_test = train_test_split(X,y)
X_train.head()

from sklearn.linear_model import LogisticRegression
clf = LogisticRegression(random_state=0, solver='lbfgs')
##在训练集上训练逻辑回归模型
clf.fit(X_train, y_train)
##查看其对应的w
print('the weight of Logistic Regression:', clf.coef_)

##查看其对应的w0
print('the intercept(w0) of Logistic Regression:', clf.intercept_)

##在训练集和测试集上分别利用训练好的模型进行预测
train_predict = clf.predict(X_train)
test_predict = clf.predict(X_test)

from sklearn import metrics
# import matplotlib.pyplot as plt

##利用accuracy（准确度）【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression is:', metrics.accuracy_score(y_train, train_predict))
print('The accuracy of the Logistic Regression is:', metrics.accuracy_score(y_test, test_predict))

##查看混淆矩阵(预测值和真实值的各类情况统计矩阵)
confusion_matrix_result = metrics.confusion_matrix(test_predict, y_test)
print('The confusion matrix result:\n', confusion_matrix_result)

# ##利用热力图对于结果进行可视化
# import seaborn as sns
# plt.figure(figsize=(8, 6))
# sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues')
# plt.xlabel('Predictedlabels')
# plt.ylabel('Truelabels')
# plt.show()

线性回归

使用uci数据集地址：http://archive.ics.uci.edu/ml/datasets/Combined+Cycle+Power+Plant

代价cost：

不调库代码实现（结果可能有点问题，需要对数据进行归一化）：

#每小时平均环境变量温度（T），环境压力（AP），相对湿度（RH）和排气真空（V），以预测工厂的每小时净电能输出（PE）。9568个数据
import pandas as pd

# 加载数据集
data= pd.read_csv('D:/Desktop/Folds5x2_pp.CSV')
data.columns=[0,1,2,3,4]
print(data.head())

X = data[[0,1,2,3]]
y = data[[4]]
X.shape

import math

MAX_FEATURE_DIMENSION = 10000
MAX_SAMPLE_NUMBER = 10000
MAX_ITERATE_NUMBER = 10000

##求导
def compute_gradient(x,y,theta,feature_number,feature_pos,sample_number):
    sum = 0.0
    for i in range(sample_number):
        res = 0.0
        for j in range(feature_number+1):
            res += x[i][j] * theta[j]
        sum += (res - y[i])*x[i][feature_pos]
    return sum/sample_number

##估价函数
def compute_cost(x,y,theta,feature_number,sample_number):
    sum = 0.0
    for i in range(sample_number):
        res = 0.0
        for j in range(feature_number+1):
            res += x[i][j] * theta[j]
        sum += (res - y[i]) * (res - y[i])
    return sum/(2*sample_number)

##梯度下降法
def gradient_descent(x,y,theta,feature_number,sample_number,alpha,count):
    for i in range(count):
        tmp = []
        for j in range(MAX_FEATURE_DIMENSION):
            tmp.append(0)
        for j in range(feature_number+1):
            tmp[j] = theta[j] - alpha * compute_gradient(x,y,theta,feature_number,j,sample_number)
        for j in range(feature_number+1):
            theta[j] = tmp[j]

        print("第",i,"次",compute_cost(x,y,theta,feature_number,sample_number))

##测试
def predict(theta,x,feature_number):
    sum = 0.0
    for i in range(feature_number+1):
        sum += theta[i]*x[i]
    return sum


if __name__ == '__main__':
    
    sample_number = X.shape[0]
    alpha = 0.0001
    count = 1500
    feature_number = 3
    theta = []
    for i in range(MAX_FEATURE_DIMENSION):
        theta.append(0)
        
    gradient_descent(X.values.tolist(),y[4].tolist(),theta,feature_number,sample_number,alpha,count)

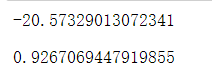
    print("[28.65,55.4,1000.25,40,95]的预测值：",predict(theta, [28.65,55.4,1000.25,40,95], feature_number))

代码实现（调用sklearen）：

#每小时平均环境变量温度（T），环境压力（AP），相对湿度（RH）和排气真空（V），以预测工厂的每小时净电能输出（PE）。9568个数据
import pandas as pd

# 加载数据集
data= pd.read_csv('D:/Desktop/Folds5x2_pp.CSV')
data.columns=[0,1,2,3,4]

X = data[[0,1,2,3]]
y = data[[4]]

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y ,test_size = 1/3.,random_state = 8)

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score

# 线性回归
lr = LinearRegression(normalize=True,n_jobs=2) 
scores = cross_val_score(lr,X_train,y_train,cv=10,scoring='neg_mean_squared_error') #计算均方误差
print(scores.mean())

lr.fit(X_train,y_train)
lr.score(X_test,y_test)

# 多项式回归
from sklearn.preprocessing import PolynomialFeatures
for k in range(1,4):
    lr_featurizer = PolynomialFeatures(degree=k) # 用于产生多项式 degree:最高次项的次数
    print('-----',k,'-----')

    X_pf_train = lr_featurizer.fit_transform(X_train)
    X_pf_test = lr_featurizer.transform(X_test)

    pf_scores = cross_val_score(lr,X_pf_train,y_train,cv=10,scoring='neg_mean_squared_error')
    print(pf_scores.mean())

    lr.fit(X_pf_train,y_train)
    print(lr.score(X_pf_test,y_test))
    print(lr.score(X_pf_train,y_train))

#当 k=1 时，回归为线性回归；
#当 k=2 时，回归为多项式回归，模型的效果比线性回归要好一点。
#当 k=3 时，已经出现过拟合现象，模型在训练集上得分很高，然而在验证集上得分很低，从交叉验证的得分结果也可以看得出来

# 正则化解决k=3的过拟合现象

lr_featurizer = PolynomialFeatures(degree=3) # 用于产生多项式 degree:最高次项的次数
X_pf_train = lr_featurizer.fit_transform(X_train)
X_pf_test = lr_featurizer.transform(X_test)

from sklearn.linear_model import Ridge

# 岭回归
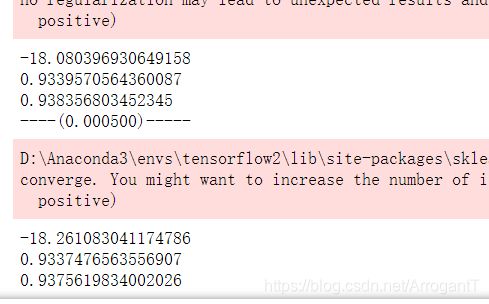
for a in [0,0.005]:
    print('----(%f)-----'%(a))
    ridge = Ridge(alpha=a,normalize=True)
    pf_scores = cross_val_score(ridge,X_pf_train,y_train,cv=10,scoring='neg_mean_squared_error')
    print(pf_scores.mean())

    ridge.fit(X_pf_train,y_train)
    print(ridge.score(X_pf_test,y_test))
    print(ridge.score(X_pf_train,y_train))


# 正则化解决k=3的过拟合现象

lr_featurizer = PolynomialFeatures(degree=3) # 用于产生多项式 degree:最高次项的次数
X_pf_train = lr_featurizer.fit_transform(X_train)
X_pf_test = lr_featurizer.transform(X_test)

# LASSO回归：
from sklearn.linear_model import Lasso

for a in [0,0.0005]:
    print('----(%f)-----'%(a))
    lasso = Lasso(alpha=a,normalize=True)
    pf_scores = cross_val_score(lasso,X_pf_train,y_train,cv=10,scoring='neg_mean_squared_error')
    print(pf_scores.mean())

    lasso.fit(X_pf_train,y_train)
    print(lasso.score(X_pf_test,y_test))
    print(lasso.score(X_pf_train,y_train))
    

线性回归运行截图：

多项式回归：

正则化解决k=3的过拟合现象：

岭回归：

LOSS回归：