【读书笔记->统计学】03-02 各种“距”和“差”-方差、标准差、标准分概念简介
变异性 “>” 分散性
继续上一篇挑选球员的例子,全局、四分位距可以告诉我们最大值和最小值之间的差值,但是无法告诉球员们得到这些最高分或最低分的频率(得高分次数多的球员好),以及球员们得到更接近数据中心的得分的频率(决赛时,得分更稳定的球员,减少得分起伏)。
可以说,全局、四分位距等方法可以帮助我们量度每批得分的分散性。但是我们还需要看出球员的稳定程度,也就是量度每批得分的“变异性”。
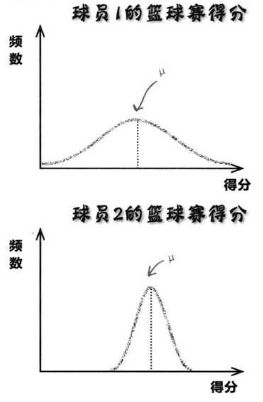
比如下图的球员1和2。
- 球员1的各个数值与均值相距甚远,可能得很低的分,也可能得很高的分,这让教练很难预测在比赛日那天是否顺利。如果不顺利,很可能球队因他而败北。
- 球员2的频数比较集中,与均值的距离近得多,变化也更少。这样教练会非常清楚该球员在每场比赛中可能的表现。
那么,有一种办法,就是求出数值与均值的平均距离就好了!数值们与均值的距离越远,说明这个球员越不稳定,不管是超低分还是超高分。
计算平均距离
如果有3个数字:1、2、9,均值为4。那么
平 均 距 离 = ( 1 至 μ ) + ( 2 至 μ ) + ( 9 至 μ ) 3 = 3 + 2 + ( − 5 ) 3 = 0 平均距离 = \frac{(1至\mu)+(2至\mu)+(9至\mu)}{3} = \frac{3 + 2 + (-5)}{3} = 0 平均距离=3(1至μ)+(2至μ)+(9至μ)=33+2+(−5)=0
( μ \mu μ表示均值)
各个数值与均值的平均距离总是为0—正负距离相互抵消。怎么办?
有人可能会说,我们直接使用正距离计算就好啦,(3+2+5)/3=3.333,不就可以啦?实际应用中,很少有统计师这样做。另外一种更常用的方式,大家应该也很熟悉,那就是方差。
方差
为了让各个距离都变成正数,我们加一个平方。
平 均 ( 距 离 ) 2 = ( 1 至 μ ) 2 + ( 2 至 μ ) 2 + ( 9 至 μ ) 2 3 = 3 2 + 2 2 + ( − 5 ) 2 3 = 12.67 平均(距离)^2 = \frac{(1至\mu)^2+(2至\mu)^2+(9至\mu)^2}{3} = \frac{3^2 + 2^2 + (-5)^2}{3} = 12.67 平均(距离)2=3(1至μ)2+(2至μ)2+(9至μ)2=332+22+(−5)2=12.67
方差:方差是量度数据分散性的一种方法,是数值与均值的距离的平方数的平均值。
方 差 = ∑ ( x − μ ) 2 n 方差 = \frac{\sum(x-\mu)^2}{n} 方差=n∑(x−μ)2
标准差
方差在量度数据的分散情况上很有用,不过其公式是距离的平方再取平均值,更难让人用平方考虑分散性。一种简单的修正方法就是—对方差取平方根,我们将此结果称为标准差。
标准差的符号为 σ \sigma σ(希腊字母“西格玛”的小写;大写“西格玛”为 Σ \Sigma Σ,表示求和)。猜得出来,那么方差就是 σ 2 \sigma^2 σ2了。
标 准 差 = 12.67 = 3.56 标准差 = \sqrt{12.67} = 3.56 标准差=12.67=3.56
可以说,典型值与均值的距离是3.56。
我们可以看出,标准差是描述典型值与均值距离的一种方法,标准差越小,数值离均值越近。标准差可能得到的最小数值为0。
书上有一段话很有趣,我快要笑死了。贴在这里给大家看看
Head First:告诉我,你和方差有什么关系吗?
标准差:问得真好笑。方差就是另一个我 — 把我平方一下,我就变成方差;取方差的平方根,我就又回来了。我们两个就像是克拉克和超人,只是少件披风而已。
方差速算法
除了求均值,然后算出每个x与均值的平方的方法,还有一种快速的方法,公式推导如下:
方 差 = ∑ ( x − μ ) 2 n = ∑ ( x − μ ) ( x − μ ) n = ∑ ( x 2 − 2 μ x + μ 2 ) n = ∑ x 2 n − 2 μ ∑ x n + ∑ μ 2 n = ∑ x 2 n − 2 μ ∗ μ + n μ 2 n = ∑ x 2 n − μ 2 方差 = \frac{\sum(x-\mu)^2}{n} \\ = \frac{\sum (x-\mu)(x-\mu)}{n} \\ = \frac{\sum (x^2-2\mu x+\mu^2)}{n} \\ = \frac{\sum x^2}{n} - \frac{2\mu\sum x}{n} + \frac{\sum \mu^2}{n} \\ = \frac{\sum x^2}{n} - 2\mu*\mu + \frac{n \mu^2}{n} \\ = \frac{\sum x^2}{n} - \mu^2 方差=n∑(x−μ)2=n∑(x−μ)(x−μ)=n∑(x2−2μx+μ2)=n∑x2−n2μ∑x+n∑μ2=n∑x2−2μ∗μ+nnμ2=n∑x2−μ2
因此, 方 差 = ∑ x 2 n − μ 2 方差 = \frac{\sum x^2}{n} - \mu^2 方差=n∑x2−μ2
相应的,标准差只需要加个根号就好了。
小知识:标准差的计量单位是什么?
标准差的计量单位与相应数据的单位相同。若以“厘米”进行计量,当标准差为1时,即表示在典型情况下,数值与均值相距1厘米。
小知识:方差的计算公式,好像除数是(n-1)来着,而不是n,是不是弄错了?
倒是没错,不过这种形式的方差仅在处理样本时使用,书后文谈及抽样时将相加说明。
有一道例题很好,大家可以做做看,利用上面的式子,对x和 μ \mu μ做出相应的改变即可求出答案。
看完这道题,是不是可以这样理解,如果公司要涨薪,全体加薪10%,那么相对来说大老板涨薪多,小员工涨薪少,只能说一直利用比例加薪的方法,会使两者差距越来越大。(直觉猜想)
标准分
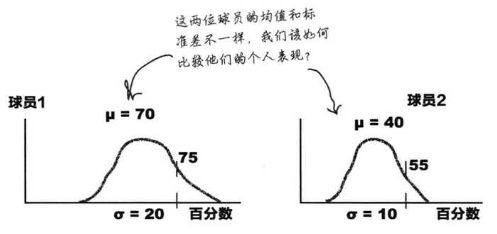
标准差可以帮助我们看出一批数据的变异情况,但是它还有其他用途。我们再看一个情境:若有两位能力不同的篮球队员,第一位投篮命中率为70%,其标准差为20%;第二位投篮命中率为40%,标准差为10%。在某次训练中,球员1投篮命中率是75%,球员2投篮命中率为55%。从球员本人的历史记录来看,哪一位球员的表现更好?
为了比较两者的“进步情况”,我们可以使用标准分(或者叫Z分)。
标准分的计算方法
使用标准分可以对不同数据集的数据进行比较,而这些不同数据集的均值和标准差各不相同—标准分是对不同环境下的相关数据进行比较的一种方法。例如,你可以使用标准分比较球员相对于其本人历史记录的表现,这有点像私人教练的一贯做法。
标准分通常以字母“z”表示,公式如下:
z = x − μ σ z = \frac{x-\mu}{\sigma} z=σx−μ
其中 μ \mu μ表示均值, σ \sigma σ表示标准差。
因此,两位球员的标准分分别为0.25和1.5:
z 1 = 75 − 70 20 = 0.25 z_1 = \frac{75-70}{20} = 0.25 z1=2075−70=0.25
z 2 = 55 − 40 10 = 1.5 z_2 = \frac{55-40}{10} = 1.5 z2=1055−40=1.5
标准分释义
通过标准分方法,可以把转换后的数值视为来自统一数据集或数据分布,从而进行比较。
可以看出,球员2的标准分比球员1更高。这意味着尽管从总体上看球员1是一位更优秀的投篮手,投篮命中率比球员2更高。但相对于本人的历史记录,却是球员2表现更好。
标准分的作用是将几个数据集转换成一个理论上的新分布,这个分布的均值为0,标准差为1,这是一种可用于进行比较的通用分布。标准分将你的数据有效地转化为符合这个模型的数据,同时确保数据的基本形状不变。
标准分可以取任意值,这些值表示相对于均值的位置。正的z分表示数值高于均值,负的z分表示数值低于均值。若z分为0,则数值等于均值本身。数值大小体现了数值与均值的距离。
概念:距离均值若干个标准差
有时候,数据师会用距离均值若干个标准差表示某个特定数值的相对位置。例如,一个数值在距离均值1个标准差的范围内 = 数值的标准分在-1到1之间;一个数值在距离均值2个标准差范围内 = 数值的标准分在-2到2之间。
小知识:标准分和异常值检测有什么关系?
答:我们可以凭主观判断确定异常值,但有时候可以将异常值定义为偏离均值三个标准差的数值。
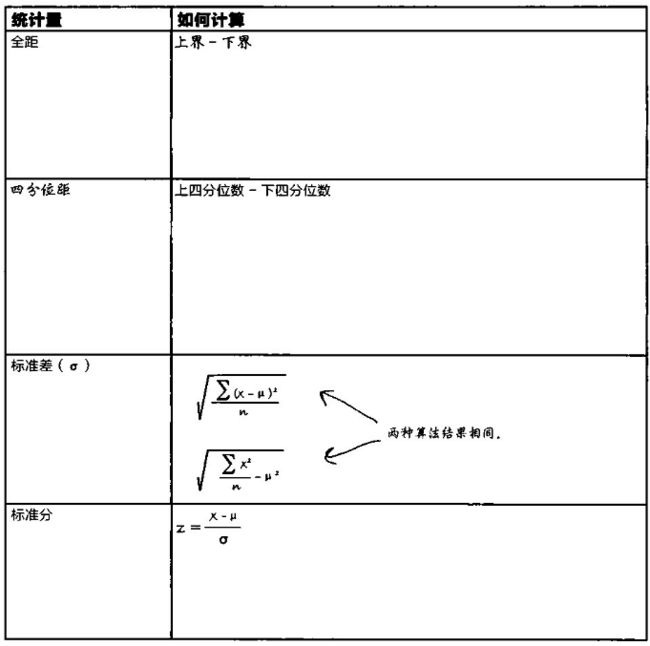
最后,书中给了全距、四分位距、标准差 σ \sigma σ、标准分的公式总结。