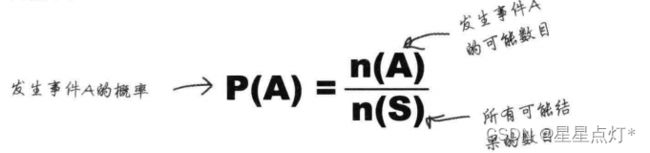【统计学知识】
一、数据类型
①定性数据(类别数据)
类别数据也称为定性数据,描述某些类的性质或者特征,不能将数据值称为数字。如:游戏种类、性别、手机种类等。
②定量数据(数值型数据)
描述的是数量,涉及的是数字。如:长度、重量、时间等。
二、图表使用
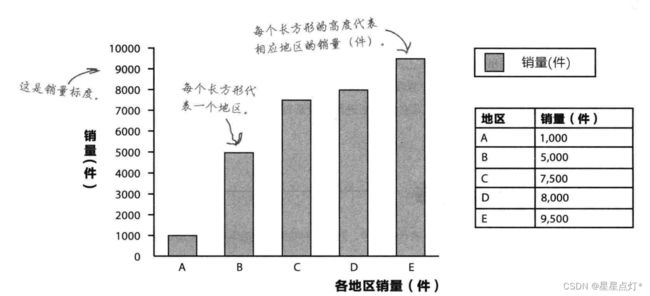
(1)条形图
①垂直条形图(频数)更常用
针对类别的频数差不多大时,可以准确的看出哪个频数最高,发现细小差别。
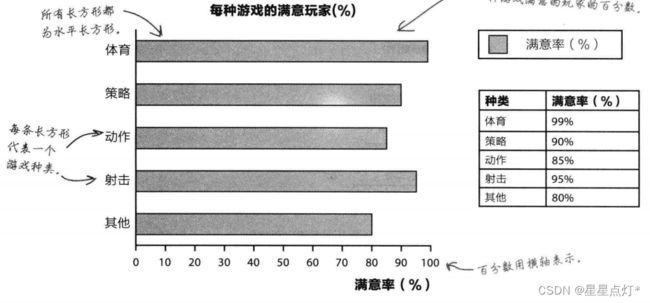
②水平条形图(百分数)
与垂直条形图类似,只是轴对掉下。
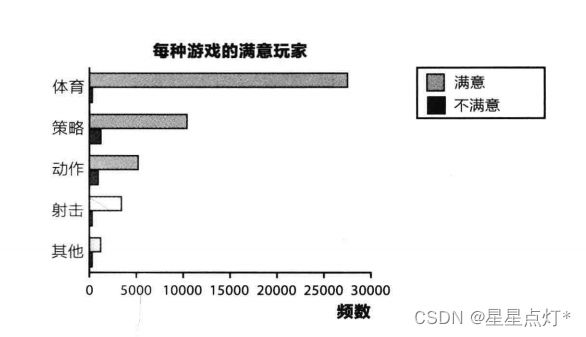
③堆积条形图
同一个图形展现多批数据进行对比。
(2)直方图(分组数据)
与条形图类型,但是频数与面积成比例,长方形间无间隔。
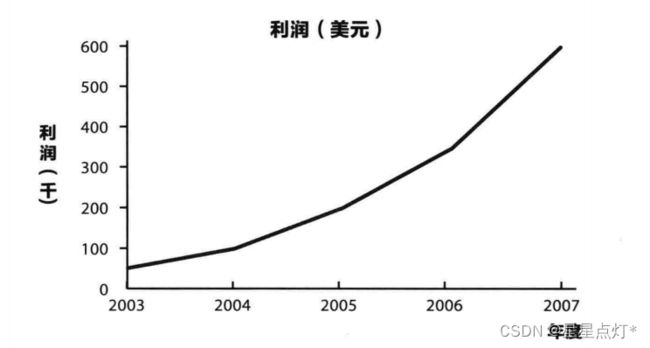
可以反映趋势,随时间变化的数值。展示数值型数据,不用于类别数据。
(4)箱线图
可以绘制各种距,根据箱线图上的线,观察到数据的偏斜程度。可以在一张图体现多批数据,便于比较。
四分位距相当于二、三四分位数
(5)维恩图(概率的图形表示)
概率的图形表示,画一个方框表示样本空间S,几个圆圈表示事件。
(6)概率树
(7)散点图(相关性)
散点图可以显示数据对之间的相关性。散点图上的点几乎成直线,为线性。有正相关、负相关、不相关。
三、统计量
(1)平均数
也称均值。把握全局,找出最具代表性的数值。一组数总和,除以组的个数。将每一个数值表示为X1,X2,X3,X4,X5……Xn
总和:SUM=X1+X2+X3+X4+X5……+Xn=![]() X
X
(2)极值(异常值)
与其他数据格格不入的极高或极低值。
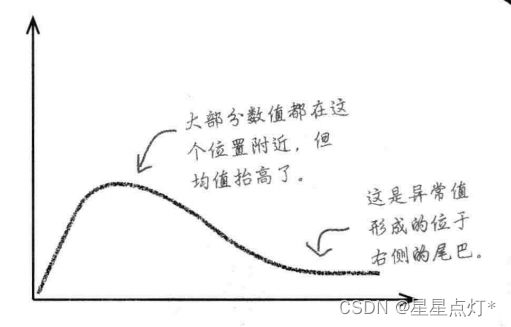
(3)偏斜数据
当数据向左或向右拉时,出现偏斜数据。
①.向右偏斜
均值偏高,向右边偏斜,形成右边拖尾现象。
②.向左偏斜
均值偏低,向左边偏斜,形成左边拖尾现象。
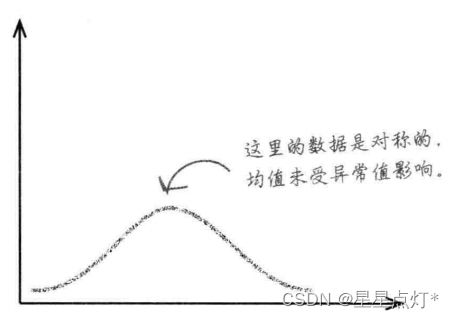
(4)对称数据
数据对称,均值位于中央,两侧数据形状大致相同。
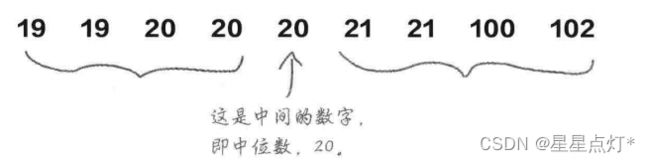
(5)中位数
当偏斜数据和异常值使均值产生误导时,表示典型值时可以采用中位数。
(6)众数
频数最大数值,数据集中的一个数值。唯一可以用于类别数据的平均数。
(7)全距(极差)
表示数据集分散程度。当中位数、平均数都一样时,可以使用全距进行衡量。全距=数据集最大值-数据集最小值,最大值为上界,最小值为下界。容易受异常值影响。
(8)四分位数(迷你距)
将数据按升序排列,分成4份等量的数据,每一份称为四分位数,最小份数为下四分位数,最大份数为上四分位数,中间四分位数为中位数。每两个四分位数的距为四分位距。
(9)平均距离
为了更好的判断,不会缺失掉部分数据,计算数值与均值的距离 。但是要防止距离之间相互抵消。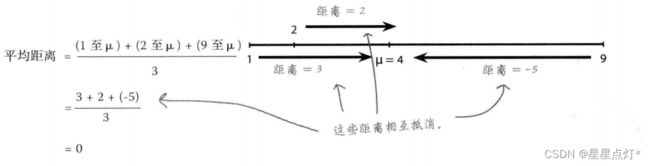
(10)方差
可以衡量变异性,量度数据分散性的一种方法,是数值与均值的距离平方数的平均值。
(11)标准差
方差的平方根。标准差越小,数值离均值的距离越小。
(12)标准分(比较不同数据集中的数值)
可以对不同数据集的数据进行比较,不同数据集的均值和标准差都不同,对相关数据进行比较的一种方法。比较两位人相对于他们本人的历史记录的表现。
四、概率
(1)概率:量度某事发展几率的一种数量指标。
S为概率空间或样本空间。所有可能发生的结果,可能发生的结果都是S的子集。
(2)事件类型
①对立事件
A事件发生,A事件不发生![]() ,A与
,A与![]() 称为对立事件。
称为对立事件。
②互斥事件
只有一个事件会发生,两个事件无任何相同之处。
③相交事件
两个时间可能同时发生。
(3)条件概率
与其他事件发生有关的某个事件发生的概率。
以B为条件,A发生的概率。
(4)全概率
事件B可能与A同时发生,也可能不与事件A同时发生。
(5)贝叶斯定理
即为条件概率,条件概率通用表达式。在无法预知每种概率情况下,可以使用此方式,是一种逆条件概率方式。
五、离散概率分布的运用
概率分布描述了一个给定变量的所有可能结果的概率。
(1)期望
期望的长期平均结果。
①随机变量:可以等于一系列值的变量。(如:随机变量为X,可以取-1,4,9,14.....),这里变量具有离散性,每个变量取确定值。(如X=-1,等于0.977)
 六、排列组合
六、排列组合
(1)排列(与顺序有关)
从群体中选取几个对象,考虑几个对象的顺序情况下,求出这几个对象选取方式的数目。需要知道每个位置站位情况。
(1)组合(与顺序无关)
从群体中选取几个对象,不考虑几个对象的顺序情况下,求出这几个对象选取方式的数目。只需要选取的对象。
七、分布
(1)几何分布、二项分布、泊松分布
(2)连续概率分布
一定特定范围的概率。(概率密度函数)
①连续数据
需要根据测量结果得到,某个变量的值可以取的是某个范围内的任意值。如:丝线的长度在10-11英寸之间,测量结果可能是10英寸、10.1英寸,10.2英寸等。连续数据包含的值可以是无穷无尽。
①正态分布(高斯分布,连续数据的理想模型)
形状钟形曲线,曲线对称,中央不为概率密度最大,越偏离均值,概率密度越小。
八、预测
(1)点估计
样本估计总体,点估计可以得到某个确切值。
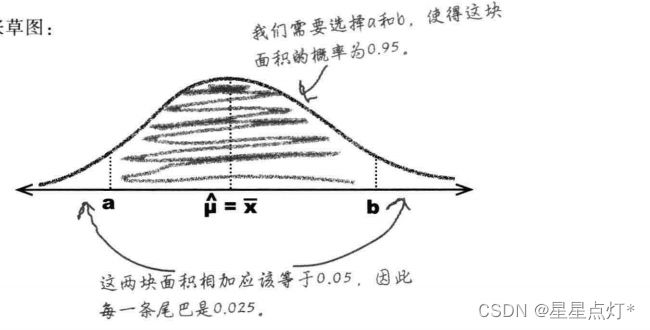
(2)置信区间
选取a、b,使得该区间包含总体均值的概率为95%。a、b数值选取,根据具体情况,使得这一区间具有可信程度。所以(a,b)为置信区间。置信水平,为有多大把握总体均值落在该区间。如该区间的置信水平为95%。
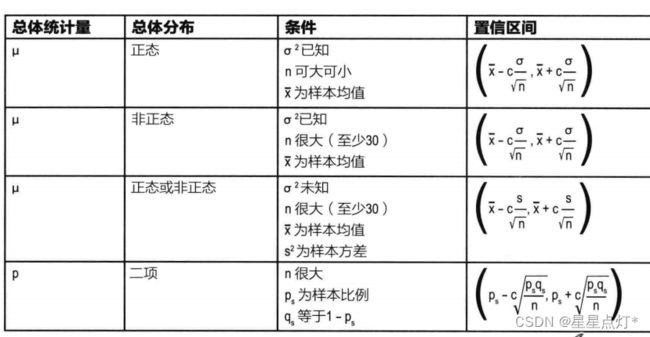
①置信区间求解
1、统计量选择,根据实际需要解决的问题:如均值。香水的持续时间均值。
2、3、4 根据分布,及置信水平95%,求出其上下限。
九、假设检验
判断他人的言论何时真、何时假。利用样本检验各种统计断言是否可能属实。
例子:
某制药公司生产一种治疗打鼾的药物,其断言在两周内治愈90%的患者。
假设检验步骤:
①查看断言
在两周内治愈90%的患者。
②查看证据
③作出决策
实现步骤:
1、断言:原假设H0,默认结论。
显著性水平:样本结果不可能达到多大时,就拒绝原假设。拒绝域。如:在置信水平95%下的概率,5%为显著性水平,则为其拒绝域。
检验选择:
1、单尾检验
①左尾检验
如果备择假设包含一个小于符号(<),使用左尾,拒绝域在数据左边(低端)。
②右尾检验
如果备择假设包含一个大于符号(>),使用左尾,拒绝域在数据右边(右端)。
2、双尾检验
备择假设包含一个不等于号(![]() ),使用双尾检验,拒绝域在数据两边。
),使用双尾检验,拒绝域在数据两边。
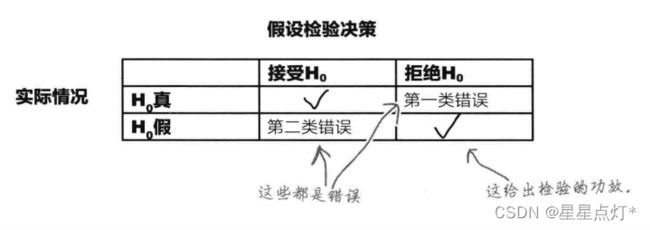
假设检验决策
①第一类错误(弃真)
H0为真,拒绝H0
②第二类错误(取伪)
H0为假,接受H0
①拟合优度
可以检验一组给定的数据与指定分布的吻合程度。例如,可以用它检验老虎机收益的观察频率与我们所期望的分布的吻合程度。
②检验两个变量的独立性
可以检验变量之间是否存在某种关系。
相关与回归
①自变量(解释变量)
其中一个变量以某种方式受到控制或被用来解释另外的变量。
②因变量(反应变量)
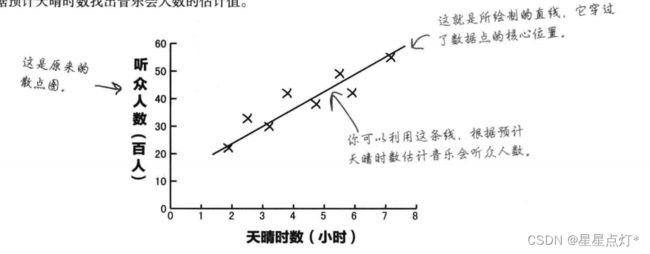
例子:天晴时数预测露天演唱会听众人数。
自变量:天晴时数
因变量:听众人数
相关关系:正相关、负相关、不相关。
相关关系与因果关系的区别
相关变量之间存在相关关系,并不意味着一个变量会影响另外一个变量,也不意味着二者存在实际关系。
例子:某个小镇的咖啡店增多,唱片机的店面减少。咖啡店与唱片店无实际的关系,即使存在相关关系,不一定存在因果关系。
最佳拟合线:
可以更好的接近所有数据点的线,使其可以进行预测。
最小二乘回归法
用于求解最佳拟合线
R方决定系数
它是可以用x变量进行解释的y变量的变异百分数。有百分之几的变异可以由预测天晴时数进行解释。R方越接近1,越能通过X预测Y;R方=1,可以从X预测Y,且无误差;R方接近0,无法预测Y。