【机器学习】多项式回归的思想以及在sklearn中使用多项式回归（含示例+代码）

一、多项式回归

回归在我们的日常生活中有着广泛的应用，线性回归法有一个很大的局限性，就是假设数据背后是存在线性关系的，但是实际上，具有线性关系的数据集是相对来说比较少的，更多时候，数据之间是具有的非线性的关系，那么我们想要用线性回归法来对非线性的数据进行处理应该怎么办呢，我们可以使用多项式回归的手段来改进线性回归法，使线性回归法也可以对非线性的数据进行处理，并进行预测。

1.1 什么是多项式回归

对于线性回归来说，对于数据的最终拟合效果，我们是想找到一条直线，使其尽可能的拟合这些数据，若只有一个特征的话，我们可以称为单变量线性回归，数学表达式如下：
$$y={\theta }_0+{\theta }_{1}x$$
其中$x$为样本特征，${\theta }_1$和${\theta }_0$为参数。

但是对于实际应用中遇到的数据来说，虽然可以使用一条直线来拟合数据，但是其分布很多时候是具有更强的非线性的关系，也就是说，使用二次曲线来拟合这些数据的话效果会更好，如果也是只有一个特征的话，那么方程可以写为：

$$y={\theta }_2{x}^2+{\theta }_{1}x+{\theta }_0$$

虽然称其为一个特征的二次方程，但是可以从另一个方向来理解这个方程，如果将$x^2$看成是一个特征，$x$看成另一个特征，这就将其看成是含有两个特征的数据集，多了一个$x^2$的特征，从这个方向来看的话，这个式子依然是一个线性回归的式子，从$x$的角度来看，就是一个非线性的方程，这样的方式就称为多项式回归。

相当于为样本多添加了几个特征，这些特征是原先样本的多项式项（像是$x^2$就是对$x$进行了平方），增加了这些特征以后就可以使用线性回归的思路，来更好的拟合原来的数据，本质上就是，求出了原来的特征而言的非线性的曲线，即为了更好地拟合数据进行了升维。

二、实战演练

展示一下部分数据：

从数据上我们看不出直观的数据分布，可视化一下：

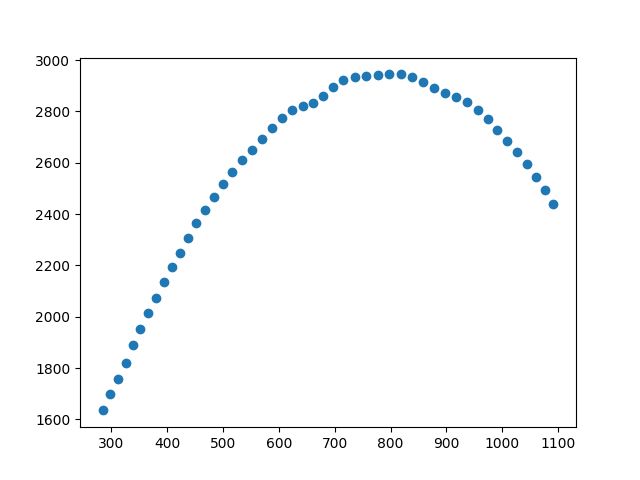
plt.scatter(data.iloc[:,0],data.iloc[:,1])
plt.show()

2.1 用线性回归的方式

首先引用LinearRegression这个类，然后实例化以后进行fit，fit传入X和y

X = np.array(data.iloc[:,0]).reshape(-1,1)
y = np.array(data.iloc[:,1]).reshape(-1,1)
estimator_1 = LinearRegression()
estimator_1.fit(X,y)
print('参数分别为:',estimator_1.coef_[0,0],estimator_1.intercept_[0])

结果为：

参数分别为: 1.0760075113688143 1831.2332236366492

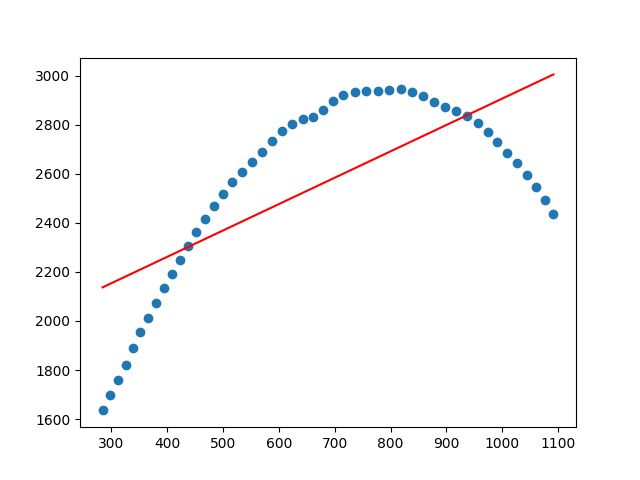
我们对结果进行可视化如下：

x = np.linspace(X.min(),X.max(),len(X))
plt.scatter(data.iloc[:,0],data.iloc[:,1])
plt.plot(x,estimator_1.coef_[0,0]*x+estimator_1.intercept_[0],c='red')
plt.show()

我们可以看到，效果很差劲！

2.2 使用多项式回归

首先加载好需要的包，再设置好的虚拟的数据集，之后引用PolynomialFeatures类，使用方法同样的，先进行实例化，传入参数degree，其表示为原来的数据集添加的最高的幂，这里设置为2，这就初始化好了，然后fit一下X，之后调用poly.transform这个方式，将其转换成多项式的特征。

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)
poly.fit(X,y)
X_2 = poly.transform(X).reshape(-1,3)
print(X_2)

[[1.00000000e+00 2.84259000e+02 8.08031791e+04]
 [1.00000000e+00 2.97780000e+02 8.86729284e+04]
 [1.00000000e+00 3.12441000e+02 9.76193785e+04]
 [1.00000000e+00 3.25961000e+02 1.06250574e+05]
 [1.00000000e+00 3.38341000e+02 1.14474632e+05]
 [1.00000000e+00 3.51006000e+02 1.23205212e+05]
 [1.00000000e+00 3.65095000e+02 1.33294359e+05]
 [1.00000000e+00 3.79756000e+02 1.44214620e+05]
 [1.00000000e+00 3.93846000e+02 1.55114672e+05]
 [1.00000000e+00 4.08219000e+02 1.66642752e+05]
 [1.00000000e+00 4.23161000e+02 1.79065232e+05]
 [1.00000000e+00 4.37534000e+02 1.91436001e+05]
 [1.00000000e+00 4.51907000e+02 2.04219937e+05]
 [1.00000000e+00 4.67419000e+02 2.18480522e+05]
 [1.00000000e+00 4.83499000e+02 2.33771283e+05]
 [1.00000000e+00 4.99577000e+02 2.49577179e+05]
 [1.00000000e+00 5.15942000e+02 2.66196147e+05]
 [1.00000000e+00 5.33445000e+02 2.84563568e+05]
 [1.00000000e+00 5.51517000e+02 3.04171001e+05]
 [1.00000000e+00 5.69303000e+02 3.24105906e+05]
 [1.00000000e+00 5.87091000e+02 3.44675842e+05]
 [1.00000000e+00 6.05163000e+02 3.66222257e+05]
 [1.00000000e+00 6.23796000e+02 3.89121450e+05]
 [1.00000000e+00 6.42698000e+02 4.13060719e+05]
 [1.00000000e+00 6.61593000e+02 4.37705298e+05]
 [1.00000000e+00 6.79077000e+02 4.61145572e+05]
 [1.00000000e+00 6.96857000e+02 4.85609678e+05]
 [1.00000000e+00 7.15484000e+02 5.11917354e+05]
 [1.00000000e+00 7.35527000e+02 5.40999968e+05]
 [1.00000000e+00 7.56130000e+02 5.71732577e+05]
 [1.00000000e+00 7.76730000e+02 6.03309493e+05]
 [1.00000000e+00 7.97333000e+02 6.35739913e+05]
 [1.00000000e+00 8.17933000e+02 6.69014392e+05]
 [1.00000000e+00 8.37948000e+02 7.02156851e+05]
 [1.00000000e+00 8.57667000e+02 7.35592683e+05]
 [1.00000000e+00 8.77380000e+02 7.69795664e+05]
 [1.00000000e+00 8.97383000e+02 8.05296249e+05]
 [1.00000000e+00 9.17676000e+02 8.42129241e+05]
 [1.00000000e+00 9.37107000e+02 8.78169529e+05]
 [1.00000000e+00 9.55957000e+02 9.13853786e+05]
 [1.00000000e+00 9.73652000e+02 9.47998217e+05]
 [1.00000000e+00 9.91055000e+02 9.82190013e+05]
 [1.00000000e+00 1.00874000e+03 1.01755639e+06]
 [1.00000000e+00 1.02643000e+03 1.05355854e+06]
 [1.00000000e+00 1.04354000e+03 1.08897573e+06]
 [1.00000000e+00 1.05979000e+03 1.12315484e+06]
 [1.00000000e+00 1.07604000e+03 1.15786208e+06]
 [1.00000000e+00 1.09171000e+03 1.19183072e+06]]

第一列的1可以看作为$x$的0次方，第2列就是原来的样本特征，第3列就是$x$的平方的特征，以此类推。

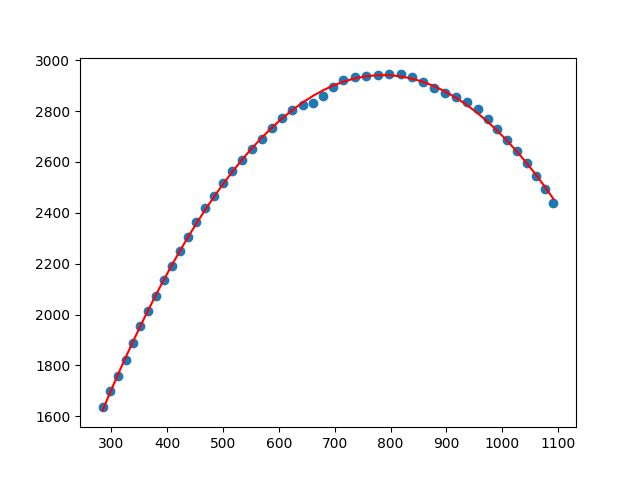
之后的操作同上，引用LinearRegression这个类，然后实例化再进行fit，拟合后，使用predict方法得到预测结果，并对其进行绘制。

estimator_2 = LinearRegression()
estimator_2.fit(X_2,y)
y_predict = estimator_2.predict(X_2)
plt.scatter(data.iloc[:,0],data.iloc[:,1])
plt.plot(X,y_predict,c='red')
plt.show()

同样的，看一下系数和截距：

[[ 0.00000000e+00  8.22812669e+00 -5.23124852e-03]] [1831.23322364]