Leetcode部分习题讲解--字符串与编码
文章目录
- LeetCode 676. 实现一个魔法字典
- LeetCode 255. 验证前序遍历二叉搜索树
- 面试题 17.17. 多次搜索
- LeetCode 32. 最长有效括号
- LeetCode 76. 最短覆盖子串
- LeetCode 468. 验证IP地址
- Leetcode 89. 格雷编码
LeetCode 676. 实现一个魔法字典

解题思路:正常的字典树匹配是要求精准匹配查找。本题允许某一位不一样。所以可以某一位没有精准匹配时,仍然向下继续遍历查找。看最终是否能匹配成功。
class Node {
public:
Node () {
flag = false;
for (int i = 0; i < 26; i++) {
next[i] = nullptr;
}
}
bool flag;
Node *next[26];
};
class Trie {
public:
Trie() {
root = new Node();
}
void insert(string &s) {
Node *p = root;
for (auto x : s) {
int ind = x - 'a';
if (p->next[ind] == nullptr) p->next[ind] = new Node();
p = p->next[ind];
}
p->flag = true;
return;
}
bool __search(string &s, int pos, Node *p, int n) {
/*
s: 要匹配查找的字符串
pos: 匹配到了s的pos位置
p: 当前匹配对应的字典树节点地址
n: 当前允许n位不一样
*/
if( pos == s.size()) return p->flag && n == 0; //当前匹配完
int ind = s[pos] - 'a';
if (p->next[ind] && __search(s, pos + 1, p->next[ind], n)) return true;
//当前位置能精准匹配,且当前位置的下一位开始往后能匹配成功
if (n) {
//当前还能允许模糊匹配
for (int i = 0; i < 26; i++) {
if (i == ind || p->next[i] == nullptr) continue;
//字典中有第i条边,并且第i条边和当前字符不是精准匹配
if(__search(s, pos + 1, p->next[i], n - 1)) return true;
}
}
//至此,模拟完了两种情况:
//一种是当前节点往下精准匹配了一步;
//另一种是当前节点模糊匹配,然后往下继续看是否能匹配成功
return false; //以上两种情况都没法匹配成功
}
bool search (string &s, int n) {
// 允许有n位不一样
//将常规查找改为递归的形式
return __search(s, 0, root, n);
/*
以下是常规的的字典树查找过程
Node *p = root;
for (auto x : s) {
int ind = x - 'a';
if (p->next[ind] == nullptr) return false;
p = p->next[ind];
}
return p->flag;
*/
}
}
private:
Node *root;
};
class MagicDictionary {
public:
MagicDictionary() {
}
Trie tree;
void buildDict(vector<string> dictionary) {
for (auto x : dictionary) {
tree.insert(x);
}
return;
}
bool search(string searchWord) {
return tree.search(searchWord, 1);
}
};
/**
* Your MagicDictionary object will be instantiated and called as such:
* MagicDictionary* obj = new MagicDictionary();
* obj->buildDict(dictionary);
* bool param_2 = obj->search(searchWord);
*/
代码提交结果:

总结:把字典树的查找过程改用递归来实现(所有的循环都可以用递归来实现)。
LeetCode 255. 验证前序遍历二叉搜索树

解题思路:结构化思维,把一个一维序列看成是一个二叉搜索树。中序遍历这颗二叉树,遍历的过程中检查是否是升序的,如果一旦发现没有升序,则是非法的,如果从始至终一直是升序的,那就是合法的。
class Solution {
public:
int pre_ind;
bool judge(vector<int> &preorder, int l, int r) {
/*
中序遍历一棵二叉树,二叉树用一维序列表示
preorder: 一维序列
l: 序列的左端点,闭区间;
r: 序列的右端点,开区间
*/
if (l >= r) return true; //空树
int ind = l + 1;
while (ind < r && preorder[ind] < preorder[l]) ind += 1;
if (!judge(preorder, l + 1, ind)) return false;
if (pre_ind != -1 && preorder[l] < preorder[pre_ind]) return false;
pre_ind = l;
if (!judge(preorder, ind, r)) return false;
return true;
}
bool verifyPreorder<ector<int> &preorder> {
pre_ind = -1;
return judge(preorder, 0, preorder.size());
}
}
代码总结:结构化思维,将一维数组看做一棵完整的二叉树。 中序遍历这颗二叉树。
面试题 17.17. 多次搜索

解题思路:本题实际为字符串匹配算法,big为文本串,smalls中的每个字符串为模式串。big是比较长的,而且是确定的,所以可以用之前讲过的sunday匹配算法。
class Solution {
public:
vector<int> sunday(string text, string pattern) {
/*
sunday字符串匹配算法,
text: 文本串
pattern: 模式串
sunday算法适合文本串确定且很长,模式串较短的情况
*/
int n = text.size(), m = pattern.size();
if (m == 0) {
vector<int> ans;
return ans;
}
// cout << m << " " << pattern << endl;
int last_pos[256];
for (int i = 0; i < 256; i++) last_pos[i] = -1;
for (int i = 0; i < m; i++) last_pos[pattern[i]] = i;
//m: 模式串的长度
vector<int> ans;
for (int i = 0; i + m <= n; i += (m - last_pos[text[i + m]])) {
// cout << "i : " << i << endl;
int flag = 1;
for (int j = 0; j < m; j++) {
if (text[i + j] == pattern[j]) continue;
flag = 0;
break;
}
if (flag) ans.push_back(i);
}
return ans;
}
// mississippi
// ppi ppi
// ppi
vector<vector<int>> multiSearch(string big, vector<string>& smalls) {
vector<vector<int>> ret;
// sunday(big, "ppi");
// cout << big << endl;
for (auto str : smalls) {
// cout << str << endl;
ret.push_back(sunday(big, str));
}
return ret;
}
};
代码提交结果:

总结:字符串匹配算法中,KMP算法适合处理流式数据,效率高;
Sunday算法适合处理文本串固定,且较长的情况;shift_and算法适合处理复杂的正则匹配。
LeetCode 32. 最长有效括号

解题思路:涉及最值问题,可以考虑使用动态规划。动态规划分三步走:状态定义,状态转移,终止条件。
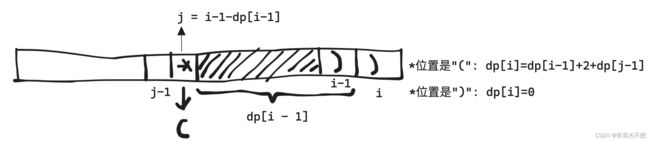
状态定义:dp[i]可以代表以i位置作为结尾时,最长有效括号的长度。
状态转移与计算:考虑dp[i]如何计算。
如果s[i]是一个左括号"(", 那么以s[i]作为结尾时,有效括号的长度一定是0,因为一定无效。
如果s[i]是一个右括号")“,s[i - 1]是一个左括号”(", 那么dp[i] 应该等于dp[i-2] + 2.

如果s[i]是一个右括号")",s[i-1]也是右括号“)”, 这个时候需要取决于i - 1 - dp[i-1]位置是左括号还是右括号:
遍历 i 在字符串中的所有位置即可。
class Solution {
public:
int longestValidParentheses(string s) {
int n = s.size();
if (n == 0) return 0;
int ans = 0, __dp[n + 5], *dp = __dp + 3;
memset(__dp, 0, sizeof(__dp)); //防止后面对dp数组的越界判断,
//直接申请一个大数组,dp在这个大数组的中间部分
//注意后面s和dp不要搞混
for (int i = 1; i < n; i++) {
if (s[i] == '(') continue;
if (s[i - 1] == '(') dp[i] = dp[i - 2] + 2;
else { //s[i - 1] == ')'
int j = i - 1 - dp[i - 1];
if (j < 0 || s[j] == ')') continue;
dp[i] = dp[j - 1] + dp[i - 1] + 2;
}
if (dp[i] > ans) ans = dp[i];
// printf("%d %d\n", i, dp[i]);
}
return ans;
}
};
代码提交结果:

总结:1. 分类讨论,动态规划; 2. 防止下标越界小技巧:申请超额数组空间。
LeetCode 76. 最短覆盖子串

解题思路:滑动窗口法,精髓在于维护窗口内部的信息。可以再窗口内部维护:当前窗口包含了t字符串的哪几种字符。关于具体如何维护,涉及到的技巧,可以看如下代码:
class Solution {
public:
string minWindow(string s, string t) {
int cnt = 0; //还没有覆盖到的字符数量
int cnts[128] = {0}; //每一个字符的覆盖情况,为负表示还差几个没有覆盖,覆盖到为0
for (auto x : t) {
cnts[x] -= 1;
if (cnts[x] == -1) cnt += 1; //第一次变成-1的时候,没覆盖到的字符 数量变化
}
int l = 0, r = 0; //滑动窗口的左右端点, 左闭右开区间
int ans_len = s.size() + 1;
int ans_l;
int flag = 0;
while (r <= s.size()) {
if (cnt > 0) { //还有字符没有被覆盖到
if (r == s.size()) break;
cnts[s[r]] += 1;
if (cnts[s[r]] == 0) cnt -= 1; //少了一个被覆盖到的字符
r += 1;
}else { //所有字符都被覆盖到了
cnts[s[l]] -= 1;
if (cnts[s[l]] == -1) cnt += 1; //多了一个被覆盖到的字符
l += 1;
}
// printf("l : %d, r : %d, cnt : %d\n", l, r, cnt);
if (cnt == 0 && r - l < ans_len) {
ans_len = r - l;
// printf("ans len : %d\n", ans_len);
ans_l = l;
flag = 1;
}
}
if (flag) return s.substr(ans_l, ans_len);
return "";
}
};
代码运行结果:

总结:1. 在滑动窗口内部维护还没有覆盖的字符串数目,以及每一个字符串是否还差几个没有被覆盖到;
2. 将s.substr()写在最后的返回中,而没有写在while循环内部动态更新结果答案,那样内存占用会多,会报“内存不足”错误。
LeetCode 468. 验证IP地址
class Solution {
public:
bool is_ipv4_valid(string ipv) {
//判断ipv4的地址字符串是否合法
if (ipv.size() > 1 && ipv[0] == '0') return false;
if (ipv.size() < 1 || ipv.size() > 3) return false;
int num = 0;
for (int i = 0; i < ipv.size(); i++) {
char c = ipv[i];
if (c < '0' || c > '9') return false;
num = num * 10 + (c - '0');
}
return num >= 0 && num <= 255;
}
bool is_ipv6_valid(string ipv) {
//判断ipv6的地址字符串是否合法
if (ipv.size() == 0) return false;
int n = ipv.size();
if (n < 1 || n > 4) return false;
for (int i = 0; i < n; i++) {
char c = ipv[i];
if (c >= '0' && c <= '9') continue;
if (c >= 'a' && c <= 'f') continue;
if (c >= 'A' && c <= 'F') continue;
return false;
}
return true;
}
string validIPAddress(string queryIP) {
int n = queryIP.size();
int ipv4_time = 0; //出现的"."的次数
int ipb6_time = 0; //出现的":"的次数
string cur_str = "";
for (int i = 0; i < n; i++) {
if (queryIP[i] == '.') {
if (ipb6_time) return "Neither";
ipv4_time += 1;
if (ipv4_time >= 4) return "Neither";
if (!is_ipv4_valid(cur_str)) return "Neither";
cur_str = "";
continue;
}else if (queryIP[i] == ':') {
if (ipv4_time) return "Neither";
ipb6_time += 1;
if (ipb6_time >= 8) return "Neither";
if (!is_ipv6_valid(cur_str)) return "Neither";
cur_str = "";
continue;
}
cur_str += queryIP[i];
}
if (ipv4_time == 3) {
if (is_ipv4_valid(cur_str)) return "IPv4";
}
if (ipb6_time == 7) {
if (is_ipv6_valid(cur_str)) return "IPv6";
}
return "Neither";
}
};
Leetcode 89. 格雷编码

题目解析:可以用构造法。因为符合要求的格雷码明显不是一种。所以如果能通过某种方式构造出一种合法的格雷码,就得到了答案。
通过n-1阶格雷码,如何构造出n阶格雷码?
假设n-1阶格雷码已经构造好如下:
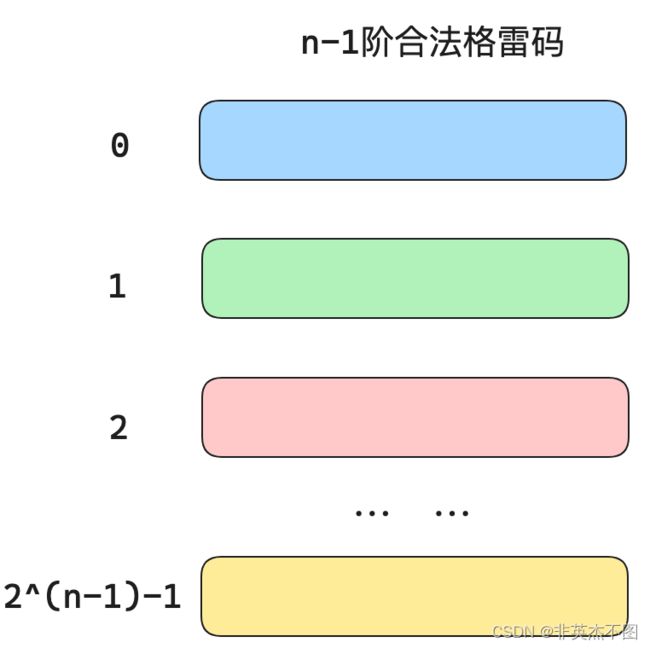
从第0位到第 2 n − 1 − 1 2^{n-1}-1 2n−1−1位都符合格雷码的序列要求。
那么n阶的格雷码和n-1阶相比,首先序列长度扩大了2倍,其次每个数字的二进制数字也多了一位。
所以可以前 2 n − 1 2^{n-1} 2n−1个数保留,在末尾加一个0,后 2 n − 1 2^{n-1} 2n−1个数对称过来,在末尾加一个1,这样一定还能满足格雷码的要求。如下图所示:
class Solution {
public:
vector<int> grayCode(int n) {
vector<int> ret(1 << n);
if (n == 0) {
ret[0] = 0; //0位直接返回0
return ret;
}
vector<int> code_n_1 = grayCode(n - 1); //构造出n-1阶格雷码
int len_n_1 = code_n_1.size();
for (int i = 0; i < len_n_1; i++) {
ret[i] = code_n_1[i] << 1; //在末尾加一个0
ret[2 * len_n_1 - i - 1] = code_n_1[i] << 1 | 1; //在二进制末尾加一个1
}
return ret;
}
};