Eigen 使用指南(入门篇)
Eigen 使用指南(入门篇)
- 1 安装Eigen
-
- 1.1 Window10(64位)+Visual Studio2017
- 2 Eigen 的使用
-
- 2.1 矩阵类Matrix
-
- 1.2.2 矩阵初始化与访问
- 2.3 矩阵和向量代数
- 2.4 数组类Array
- 2.5 块操作
- 2.6 库函数
- 附录
1 安装Eigen
bilibili配套安装视频
Eigen源码下载:http://eigen.tuxfamily.org/index.php?title=Main_Page
建议下载最新稳定版,Windows环境下可下载“zip”格式的文件,Linux环境可下载“tar.gz”格式的文件。下面的分析将以Eigen3.3.7为例,介绍Eigen的安装。

1.1 Window10(64位)+Visual Studio2017
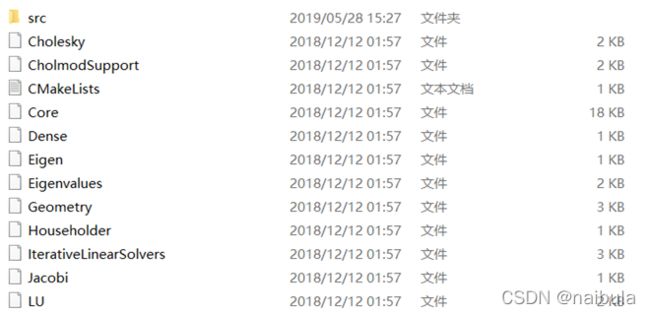
解压源码,得到一个名字很长的文件夹,进入该文件夹,即可看到如下文件目录。在下图中,Eigen文件夹是我们需要使用的源文件目录,通常只要将该文件复制到对应的工程即可使用Eigen库。进入Eigen文件夹,可以看到有一个Dense文件,这是一个头文件接口,在使用Eigen库的源码中需要包含该头文件。

下面介绍Eigen如何使用的一个简单用例,但是此处不解释代码。
- 打开Visual Studio2017,新建一个C++项目(依次点击 文件->新建->项目),养成自己设置工程路径的好习惯,一般不将工程建在C盘,如图1-4;
- 进入到工程存储的位置,查看工程目录,熟悉vs创建的目录结构,以创建一个名为Eigen_Test项目为例,其目录结构如图1-5所示;
- 在vs2017中添加源文件,命名为main.cpp,main.cpp中的内容为附录“source1.1”,源码中包含了Dense文件,这个文件是使用Eigen库的接口;
- 将图1-2中的Eigen文件夹复制到图1-5Eigen_Test解决方案目录下,如图1-6所示;
- 编译运行,如果可以正常编译运行,那么说明Eigen库已经成功配置。
2 Eigen 的使用
bilibili配套Eigen入门视频教程。
在Eigen,中所有的矩阵和向量都是Matrix模板类的对象,向量只是一种特殊的矩阵。
2.1 矩阵类Matrix
Matrix类总共有六个模板参数首先只介绍前三个参数,剩下的三个参数有其默认值。三个强制型的参数如下:
Matrix
- Scalar是scalar类型,如想要构造一个单精度的浮点类型矩阵,可以选择float。所有支持的Scalar类型包括:float、double、int、std::complex(float)、和自定义类型。
- RowsAtCompileTime和ColsAtCompileTime分别表示行数和列数,要求这两个参数在编译时已知。
在Eigen中提供宏定义来便捷的访问一些常用的类型,如:
typedef Matrix<float, 4, 4> Matrix4f;
typedef Matrix<float, 3, 1> Vector3f;
typedef Matrix<int, 1, 2> RowVector2i;
当然,Eigen库并不局限于那些矩阵维数在编译时已知的情形。RowsAtCompileTime和ColsAtCompileTime可以取一个特殊的值Dynamic,这表示矩阵的维度在编译时是未知的,必须作为一个运行时变量来处理。在Eigen术语中,Dynamic称为动态大小(dynamic size),而运行时已知的大小称为固定大小(fixed size)。
创建一个双精度的动态矩阵
typedef Matrix
创建一个整型列向量
typedef Matrix
Matrix的另外三个模板参数是可以选择的,完整的参数如下:
Matrix<typename Scalar,
int RowsAtCompileTime,
int ColsAtCompileTime,
int Options = 0,
int MaxRowsAtCompileTime = RowsAtCompileTime,
int MaxColsAtCompileTime = ColsAtCompileTime>
- Options是一个位域,它的值只能取RowMajor、ColMajor,分别表示行优先存储、列优先存储。默认情况下是使用列优先存储,一般地Eigen库在列优先存储的情况下效率要高。Eigen的存储形式的指定,只是影响矩阵在内存的形式,不会影响矩阵的访问习惯。
- MaxRowsAtCompileTime和MaxColsAtCompileTime用于指定矩阵的维数的最大值。尽管有时候不知道矩阵的确切大小,但在编译时已经知道了矩阵维数的上界,那么可以指定这两个参数来避免动态内存分配。
1.2.2 矩阵初始化与访问
Eigen库提供了默认构造函数,它不会提供动态内存的分配,也不会初始化任何矩阵的值。Eigen类型可以这样使用:
Matrix3f a;
MatrixXf b;
这里
- a是一个3*3的矩阵,矩阵的元素都没有被初始化;
- b是一个动态矩阵,它的大小是0*0,也就是说还没有为该矩阵分配内存。
构造函数提供指定矩阵大小的重载。对矩阵来说,第一个参数是矩阵的行数。对向量来说只需指定向量的大小。它会分配矩阵或向量所需的内存的大小,但是不会初始化他们的值。
MatrixXf a(10,15);
VectorXf b(30);
- a是一个10*15的动态矩阵,内存进行了分配,但没有初始化;
- b是一个大小为30的动态数组,但没有初始化。
Eigen库重载圆括号()访问矩阵或者向量的元素,序号从0开始。Eigen库不支持使用方括号[]访问矩阵的元素(向量除外)。
MatrixXd m(2,2);
m(0,0) = 3;
VectorXd v(2);
v(0) = 4;
逗号表达式初始化
Matrix3f m;
m << 1, 2, 3,
4, 5, 6,
7, 8, 9;
std::cout << m;
可以使用rows()、cols()、size()访问矩阵当前大小,使用resize()重置矩阵的大小。如果矩阵的大小没有变化,那么resize()操作没有任何影响。如果矩阵的大小改变了,那么矩阵的值可能会改变。如果你想在重设大小过程中不改变矩阵的值使用conservativeResize()。
使用赋值操作符“=”,Eigen将左操作数的大小重置为右操作数的大小。
2.3 矩阵和向量代数
加减法:重载C++中“+”、“-”、“+=”、“-=”操作符,要求左右操作数的维度相同。不允许一个向量加上或者减去一个数。
数乘与数除:重载C++中“”、“/”、“=”、“/=”操作符,支持矩阵和向量乘以或者除以一个数。
转置与共轭:转置aT、共轭 、共轭转置aH分别通过transpose()、conjugate()、adjoint()实现。调用格式a.transpose(),a.conjugate(),a.adjoint()。对于实数而言,共轭没有任何影响,共轭转置等价于转置。使用a = a.transpose()可能会出现错误,这是因为Eigen在进行转置或者共轭操作时,会同时写左操作数,从而得到意想不到的结果。要实现这种功能可以使用a.transposeInPlace()。类似的,也支持adjointInPlace()。
矩阵-矩阵与矩阵-向量乘法:由于在Eigen中向量只是特殊的矩阵,因此只需重载“*”、“*=”即可实现矩阵和向量的乘法。如果你担心m=mm会导致混淆,现在可以消除这个疑虑,因为Eigen以一种特殊的方式处理矩阵乘法,编译m=mm时,作为
tmp = m*m;
m = tmp;
点积和叉乘:点积又可以称为内积,Eigen分别使用dot()和cross()来实现内积和向量积。叉乘只适用于三维向量。
Vector3d v(1,2,3);
Vector3d w(0,1,2);
v.dot(w);
v.cross(w);
基础的代数计算:mat.sum()计算所有矩阵元素的和,mat.pro()计算所有元素的连乘积,mat.mean()计算所有元素的平均值,mat.minCoeff()计算矩阵元素的最小值,mat.maxCoeff计算矩阵元素的最大值,mat.trace()计算矩阵的迹。计算最大值和最小值的函数支持返回最大值和最小值的位置:
Matrix3f m = Matrix3f::Random();
std::ptrdiff_t i, j; //ptrdiff_t是stddef.h中用于表示两个指针见的间隔的数据类型,是有符号型
float minOfM = m.minCoeff(&i,&j);
注意:
- 在计算过程中如果由于矩阵维度不满足相应的条件,那么Eigen库可以在编译时检查出静态矩阵维度的矛盾,对于动态矩阵有相应动态检查方法,如果出现维度矛盾可能会使程序崩溃。
- 以上的操作都不会影响操作数本身。
- 通过“.”操作符调用的操作可以作为左值,当然这在一般情况下是没多大意义的。
2.4 数组类Array
Array类提供通常意义上的数组,它提供一些方便的对元素的非线性操作。例如让所有元素都加上一个常量,或者让两个Arrays的值对应相乘。
Array类模板与Matrix相似,其含义参见Matrix类介绍。Array在其存储形式上具有矩阵的形式,只是说Array支持的运算和Matrix不一样。
Array<typename Scalar, int RowsAtCompileTime, int ColsAtCompileTime>;
Array<float,Dynamic,1> ArrayXf;
Array<float,3,1> Array3f;
Array<double,Dynamic,Dynamic> ArrayXXd;
访问Array中的值的方式和Matrix是一样的。下面介绍和Matrix不一样的操作:
加减乘除:将对应位置元素相加(减、乘、除)。
ArrayXXf a(2,2);
ArrayXXf b(2,2);
a << 1,2,3,4;
b << 5,6,7,8;
cout<<a*b;
输出结果为:
5 12
21 32
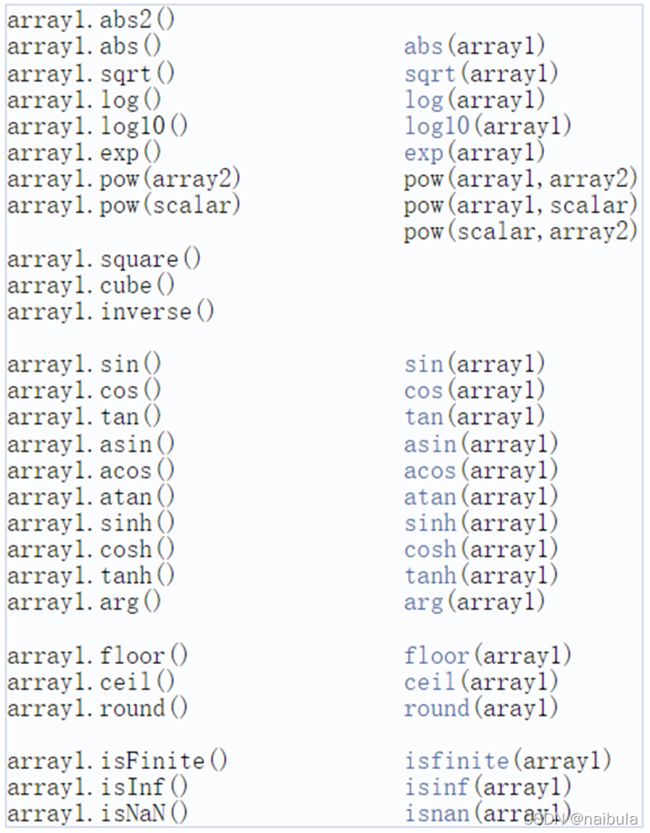
平方根、绝对值:通过调用sqrt()、abs()函数,a.abs()。
求两个矩阵的最小值:a.min(b),要求a和b的维度相同,求对应位置的两个数的最小值。
Eigen支持的数组元操作见图2-1所示。那么,如何选择Matrix和Array呢?如果要支持线性代数的操作,就选择Matrix;如果要进行coefficient-wise操作,就选择Array。如果又要支持线性代数操作,又要支持coefficient-wise操作,那么就可以使用.array()和.matrix()实现类型的转换,这种转换是没有计算代价的。这些操作也不会改变调用该函数的矩阵或者数组本身而是返回一个副本。
2.5 块操作
块是矩阵的一个矩形区域,块表达式可以是左值也可以是右值。最常用的是block()操作,它有两个版本:
matrix.block(i,j,p,q);//动态大小的块
matrix.block<p,q>(i,j);//固定大小的块
i、j表示块的起始位置(块的左上角元素在矩阵中的角标),p、q表示块的大小。固定大小的块在运行时效率要高。
Eigen::MatrixXf m(4,4);
m << 1, 2, 3, 4,
5, 6, 7, 8,
9,10,11,12,
13,14,15,16;
cout << m.block(0,0,i,i) << endl;
结果:
Block of size 3x3
1 2 3
5 6 7
9 10 11
block()操作也可用于左值:
MatrixXd m(3,3);
VectorXd v(3);
m << 1, 2, 3,
4, 5, 6,
7, 8, 9;
v << 11, 12, 13;
m.block(0, 0, 3, 1) = v;
cout << m.block(0,0,3,1) << endl;
结果:
11
12
13
block()操作支持任意的块操作,对于一些特殊的访问Eigen也提供了API。
Block operation Method
ith row * matrix.row(i);
jth column * matrix.col(j);
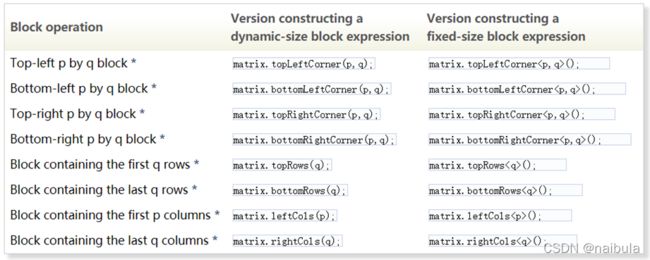
同样的,row()操作和col ()操作既可以是左值又可以是右值。除此之外,Eigen还提供了访问一些特殊位置的块的快捷操作,如图2-2所示。
对于向量或者说一维数组,Eigen也提供了特殊的块操作,如图1-9所示。这些块操作也有静态和动态两个版本。v.head(n)可以访问向量的头n个元素,v.tail(n)可以访问向量的尾n个元素,v.segment(i,j)可以访问从标号为i开始的j个元素。
2.6 库函数
随机向量或矩阵生成
使用Random函数,生成双精度的随机数在-1到1之间,生成整数的随机数在某一个负整数到某一个正整数之间与机器有关。样例:
MatrixXd m=MatrixXd::Random(2,3);
VectorXi v= VectorXi::Random(1);
零向量或矩阵生成
使用Zero()函数,生成值全为零的矩阵或向量。
MatrixXd m=MatrixXd::Zero(2,3);
VectorXi v= VectorXi::Zero(1);
生成单位矩阵
使用Identity()函数,生成单位矩阵或准单位矩阵。
MatrixXd m= MatrixXd::Identity(5,5);
MatrixXd m= MatrixXd::Identity(5,4);
附录
#include > map1(p1, iRow1, iCol1);
//Eigen::Map< Eigen::Matrix > map2(p2, iRow2, iCol2);
//Eigen::Map< Eigen::Matrix > map3(p3, iCol1, iCol2);
//Row first
Eigen::Map< Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor> > map1(p1, iRow1, iCol1);
Eigen::Map< Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor> > map2(p2, iRow2, iCol2);
Eigen::Map< Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor> > map3(p3, iCol1, iCol2);
map3 = map1 * map2;
}
int main(int argc, char* argv[])
{
Eigen::MatrixXd m(2, 2);
m(0, 0) = 1;
m(0, 1) = 2;
m(1, 0) = m(0, 0) + 3;
m(1, 1) = m(0, 0) * m(0, 1);
std::cout << m << std::endl << std::endl;
return 0;
}