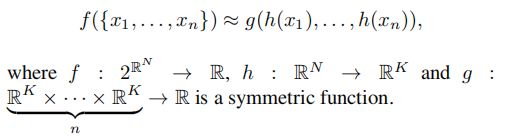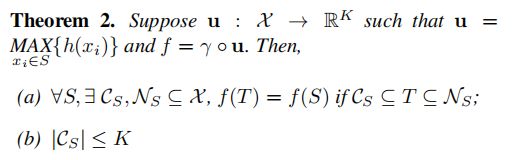PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation(2017)
基础:
Voxel:体素,是体积元素(Volume Pixel)的简称,是数字数据于三维空间分割上的最小单位,概念上类似二维空间的最小单位——像素,像素用在二维计算机图像的影像数据上。有些真正的三维显示器运用体素来描述它们的分辨率,举例来说:可以显示512×512×512体素的显示器。
点云的特征:几何数据结构、不规则、可以转换为3D体素网格或图片集合处理但会产生不必要的数据量(不需要的数据太多了)及其他问题
Hausdorff distance :豪斯多夫距离,量度度量空间中真子集之间的距离
设 X和 Y是度量空间 M的两个真子集,那么豪斯多夫距离 dH( X, Y)是最小的数 r使得 X的闭 r—邻域包含 Y, Y的闭 r—邻域也包含 X。
1. Introduction
PointNet:consumes point clouds directly
网络设计考虑的问题:
a point cloud is just a set of points and therefore invariant to permutations of its members, necessitating certain symmetrizations in the net computation. Further invariances to rigid motions also need to be considered.
点的排列不变性,对称、刚性运动的不变性都需要考虑
输入:point clouds;输出:class labels for the entire input,or per point segment labels
方法的关键是,对称函数、最大池化
网络学会了用一组稀疏的关键点来概括一个输入点云,根据可视化,这大致相当于物体的骨架。
The key contributions :
• We design a novel deep net architecture suitable for consuming unordered point sets in 3D;
• We show how such a net can be trained to perform 3D shape classifification, shape part segmentation and scene semantic parsing tasks;
• We provide thorough empirical and theoretical analysis on the stability and effificiency of our method;
• We illustrate the 3D features computed by the selected neurons in the net and develop intuitive explanations for its performance.
2. Related Work
Deep Learning on 3D Data
3D数据的多种表现形式:
Volumetric CNNs
Multiview CNNs
Spectral CNNs
Feature-based DNNs
Deep Learning on Unordered Sets
read-process-write network
3. Problem Statement
点云表示方式,一个3D点集合
each point P i is a vector of its ( x, y, z ) coordinate plus extra feature channels such as color, normal etc
为了简单以及清晰,pointnet只使用(x, y, z)坐标作为点的通道
对于分类任务:输入:either directly sampled from a shape or pre-segmented froma scene point cloud.
输出:K类的K个分数
对于语义分割:输入:a single object for part region segmentation, or a sub-volume from a 3D scene for object region segmentation
输出: n × m scores,n个点,m个 semantic subcategories
4. Deep Learning on Point Sets
4.1. Properties of Point Sets in

欧几里得空间点集的三个主要性质: Unordered(无序)、 Interaction among points(点与点之间的相互作用)、Invariance under transformations(学习到的表示对某些变换的不变性)
4.2. PointNet Architecture
Symmetry Function for Unordered Input
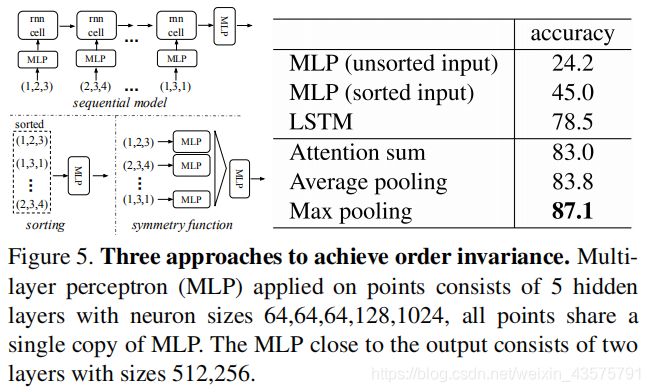
In order to make a model invariant to input permutation, three strategies exist:
1) sort input into a canonical order;
2) treat the input as a sequence to train an RNN, but augment the training data by all kinds of permutations;
3) use a simple symmetric function to aggregate the information from each point.
分析结果是前两种都不行,选用第三种。
approximate a general function defifined on a point set by applying a symmetric function on transformed elements in the set:
approximate h by a multi-layer perceptron network and g by a composition of a single variable function and a max pooling function.(用mlp近似h,单一变量函数和最大池化近似g)
Local and Global Information Aggregation
After computing the global point cloud feature vector, we feed it back to per point features by concatenating the global feature with each of the point features.(就是point_features = for point in points:concat(point_feature,global_feature))
Joint Alignment Network
The semantic labeling of a point cloud has to be invariant if the point cloud undergoes certain geometric transformations, such as rigid transformation.(要求点云的语义标记对某些几何变换不变)
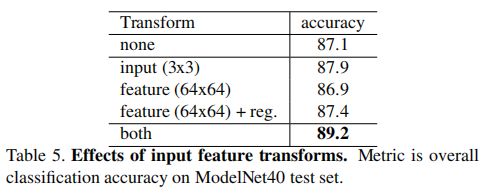
A natural solution is to align all input set to a canonical space before feature extraction.(抽取特征前把所有输入集合对齐到特定空间)[1]
本文采用的方式相对简单,即:predict an affifine transformation matrix by a mini-network (T-net)(用T-net预测一个仿射变换矩阵,并作用于输入点坐标)
This idea can be further extended to the alignment of feature space, as well. We can insert another alignment network on point features and predict a feature transformation matrix to align features from different input point clouds.(同样的想法扩展到特征空间对齐,预测一个特征变换矩阵对齐来自不同点云的特征。)
但是由于特征空间变换矩阵高维度以及增加优化困难,所以softmax training loss中加一个正则项:
A is the feature alignment matrix predicted by a mini-network. A接近正交矩阵,这样不会损失输入信息。
所以,解决点云语义标记对几何变换不变的问题的方法是,在[1]的思想下,利用mini-network生成affifine transformation matrix对齐输入点,生成 feature alignment matrix对齐特征。优化需要,增加正则项,A接近正交。
4.3. Theoretical Analysis
Universal approximation
the universal approximation ability of our neural network to continuous set functions.(对连续集函数的万能逼近能力)
The key idea is that in the worst case the network can learn to convert a point cloud into a volumetric representation, by partitioning the space into equal-sized voxels. (最坏的情况也能把点云转换成体积表示)
Bottleneck dimension and stability
网络的表达能力受最大池层的维数的影响很大
5. Experiment
3D Object Classifification
ModelNet40
acc:86.2(avg. class) 89.2(overall )
3D Object Part Segmentation
ShapeNet part dataset
Evaluation metric: mIoU on points
5.2. Architecture Design Analysis
Supplementary
1、transformation network
输入: raw point cloud
输出:3x3矩阵
结构:
It's composed of a shared MLP (64 , 128, 1024) network (with layer output sizes 64, 128, 1024) on each point, a max pooling across points and two fully connected layers with output sizes 512 , 256. The output matrix is initialized as an identity matrix. All layers, except the last one, include ReLU and batch normalization.
def input_transform_net(point_cloud, is_training, bn_decay=None, K=3):
""" Input (XYZ) Transform Net, input is BxNx3 gray image
Return:
Transformation matrix of size 3xK """
batch_size = point_cloud.get_shape()[0]
num_point = point_cloud.get_shape()[1]
input_image = tf.expand_dims(point_cloud, -1)
net = tf_util.conv2d(input_image, 64, [1, 3], padding='VALID', stride=[1, 1], bn=True, is_training=is_training,
scope='tconv1', bn_decay=bn_decay)
net = tf_util.conv2d(net, 128, [1, 1], padding='VALID', stride=[1, 1], bn=True, is_training=is_training,
scope='tconv2', bn_decay=bn_decay)
net = tf_util.conv2d(net, 1024, [1, 1], padding='VALID', stride=[1, 1], bn=True, is_training=is_training,
scope='tconv3', bn_decay=bn_decay)
net = tf_util.max_pool2d(net, [num_point, 1], padding='VALID', scope='tmaxpool')
net = tf.reshape(net, [batch_size, -1])
net = tf_util.fully_connected(net, 512, bn=True, is_training=is_training, scope='tfc1', bn_decay=bn_decay)
net = tf_util.fully_connected(net, 256, bn=True, is_training=is_training, scope='tfc2', bn_decay=bn_decay)
with tf.compat.v1.variable_scope('transform_XYZ') as sc:
assert (K == 3)
weights = tf.compat.v1.get_variable('weights', [256, 3 * K], initializer=tf.constant_initializer(0.0), dtype=tf.float32)
biases = tf.compat.v1.get_variable('biases', [3 * K], initializer=tf.constant_initializer(0.0), dtype=tf.float32)
biases = biases.assign_add(tf.constant([1, 0, 0, 0, 1, 0, 0, 0, 1], dtype=tf.float32))
transform = tf.matmul(net, weights)
transform = tf.nn.bias_add(transform, biases)
transform = tf.reshape(transform, [batch_size, 3, K])
return transform fc层,输出256维,dropout = 0.3
BN层衰减0.5 -> 0.99
adam,初始lr=0.001,momentum=0.9,batchsize=32
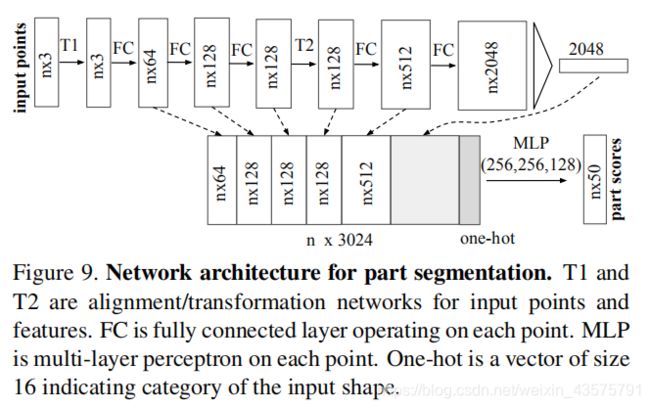
PointNet Segmentation Network
基本分割网络,就是前面的图上面那个,语义分割使用的是基本分割网络
部分分割,shape part segmentation稍作改变如下:
add a one-hot vector indicating the class of the input,增加神经元记忆跳跃连接,融合不同层的局部信息
Baseline 3D CNN Segmentation Network
D. Details on Detection Pipeline
G. Proof of Theorem
略
[1] M. Jaderberg, K. Simonyan, A. Zisserman, et al. Spatial transformer networks.(点变换到特定空间使得对某些几何变换具有不变性)
geometric data structure
3D voxel grids
point clouds data augmentation(random rotation around up-axis and jittering)
missing points
3D CNN Segmentation Network:VoxNet(a representative architecture for volumetric representation ),3DShapeNets