455.分发饼干 376. 摆动序列 53. 最大子序和
455.分发饼干 376. 摆动序列 53. 最大子序和
455.分发饼干
力扣题目链接(opens new window)
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:
- 输入: g = [1,2,3], s = [1,1]
- 输出: 1 解释:你有三个孩子和两块小饼干,3 个孩子的胃口值分别是:1,2,3。虽然你有两块小饼干,由于他们的尺寸都是 1,你只能让胃口值是 1 的孩子满足。所以你应该输出 1。
示例 2:
- 输入: g = [1,2], s = [1,2,3]
- 输出: 2
- 解释:你有两个孩子和三块小饼干,2 个孩子的胃口值分别是 1,2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出 2.
提示:
- 1 <= g.length <= 3 * 10^4
- 0 <= s.length <= 3 * 10^4
- 1 <= g[i], s[j] <= 2^31 - 1
思路:贪心
分发饼干
思路:贪心算法
贪心算法没有像递归和回溯算法一样的固定模板去解决
只能想到局部最优解,然后推到全局最优解,同时想不到推翻的反例
此题目的局部最优解有两种
1.胃口小的小孩,先拿到满足胃口的最小饼干
2,胃口大的小孩,先拿到满足胃口的最大饼干
这里采用第一种局部最优解
1.先对胃口g[i]和饼干 s[j]数组升序排序
2.从头遍历胃口数组,再从头遍历饼干数组,找到满足胃口的最小饼干。
3.遍历饼干数组引入index变量,index为当前使用的饼干数组下标。一旦该饼干被使用,那么index+1,避免重复使用饼干
3.记录满足胃口的饼干数量num
时间复杂度:O(mn)
空间复杂度:O(1)
代码如下
public int findContentChildren(int[] g, int[] s) {
int num = 0;
int index = 0;
if (g == null || g.length == 0 || s == null || s.length == 0)// 边缘条件
return num;
Arrays.sort(g);// 胃口g[i]和饼干 s[j]数组升序排序
Arrays.sort(s);
for (int i = 0; i < g.length; i++) {//从头遍历胃口数组
for (int j = index; j < s.length; j++) {
if (s[j] >= g[i]) {
index = j + 1;
num++;
break;
}
}
}
return num;
}
思路:贪心优化
贪心:优化
第一版本的代码对使用了两个for循环解决问题,时间复杂度高一些
但其实一个for循环就可以解决问题
如果使用一个for循环,需要改变局部最优解的思路。先喂饱胃口大的
因为采用一个for循环,只会对胃口遍历,而不会对饼干遍历。不能保证胃口小的小孩,先拿到满足胃口的最小饼干。
比如说第一个饼干很小,不满足第一个小孩需求,那么for循环就会走第二个小孩,不会给第一个小孩分配饼干
所以只能保证胃口大的小孩,先拿到满足胃口的最大饼干,或者胃口口小的小孩拿到最小的饼干,但并不一定满足胃口
时间复杂度:O(mlogm+nlogn) Arrays.sort(g)排序使用的是归并排序,时间复杂度为nlogn
空间复杂度:O(1)
代码如下
public int findContentChildren(int[] g, int[] s) {
int num = 0;
int index = s.length - 1;
if (g == null || g.length == 0 || s == null || s.length == 0)// 边缘条件
return num;
Arrays.sort(g);// 胃口g[i]和饼干 s[j]数组升序排序
Arrays.sort(s);
for (int i = g.length - 1; i >= 0; i--) {//从头遍历胃口数组
if (index >= 0 && s[index] >= g[i]) {
index--;
num++;
}
}
return num;
}
376.摆动序列
力扣题目链接(opens new window)
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
示例 1:
- 输入: [1,7,4,9,2,5]
- 输出: 6
- 解释: 整个序列均为摆动序列。
示例 2:
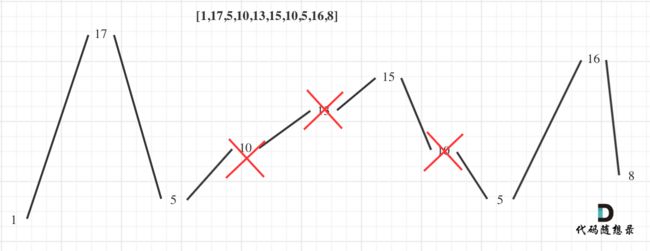
- 输入: [1,17,5,10,13,15,10,5,16,8]
- 输出: 7
- 解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
示例 3:
- 输入: [1,2,3,4,5,6,7,8,9]
- 输出: 2
思路
题目要求求出整数序列的最长子序列长度,而且子序列可以从从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
这句话不太好理解,使用图片来表达。
删除规则为:保留峰值,删除单调坡除了首尾两端元素
套用贪心的思路
局部最优:对每一个小单调区间,删除首尾两端以外的所有元素
整体最优:获得最长子序列
但是在实际操作中,并不需要删除序列里面元素的值,因为我们只需要统计长度而已
所以只要坡度存在波动,即遍历的下标 ,计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i])。
记录峰值条件:即prediff > 0 && curdiff<0 或 prediff < 0 && curdiff> 0
为了避免平坡的情况,增加考虑的情况,只需要对数组相邻元素去重即可
代码如下
// 时间复杂度 o(n)
// 空间复杂度o(n)
public int wiggleMaxLength(int[] nums) {
// 数组相邻元素去重
List<Integer> list = new ArrayList<>();
if (nums.length == 0) {
return 0;
}
int prev = nums[0];
list.add(prev);
for (int i = 1; i < nums.length; i++) {
if (nums[i] != prev) {
list.add(nums[i]);
prev = nums[i];
}
}
if (list.size() == 0 || list.size() == 1 || list.size() == 2) // 特殊情况处理
return list.size();
if (list.size() == 1 || list.size() == 2) {
return list.size();
}
int num = 2;// 摆动序列的个数
int curDiff = 0; // 后一对差值
int preDiff = 0;// 前一对差值
for (int i = 1; i < list.size() - 1; i++) {
preDiff = list.get(i) - list.get(i - 1);
curDiff = list.get(i + 1) - list.get(i);
if ((preDiff > 0 && curDiff < 0) || (preDiff < 0 && curDiff > 0)) {
num++;
}
}
return num;
}
53.最大子序和
力扣题目链接(opens new window)
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
- 输入: [-2,1,-3,4,-1,2,1,-5,4]
- 输出: 6
- 解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
思路
思路:暴力
定义双重for循环,以第一层For循环为起始位置,在第二层for循环遍历数组,记录连续子数组的最大值
思路:贪心算法
这题的贪心思路不好想
贪心算法的目的是从【局部最优】推出【整体最优】
局部最优:当前连续子数组总和为负数时,会减小连续子数组总和val,所以重新寻找子数组起始位置。位置为当前位置向后移动一位
整体最优:选取最大连续和
时间复杂度:o(n)
空间复杂度:o(1)
代码如下
public int maxSubArray(int[] nums) {
int count = 0;// 连续子数组当前和
int maxCount = Integer.MIN_VALUE;// 连续子数组最大和
for (int i = 0; i < nums.length; i++) {
count += nums[i];
if(count > maxCount){
maxCount = count;
}
if (count < 0) {// 当前连续子数组总和为负数时,所以重新寻找子数组起始位置
count = 0;
}
}
return maxCount;
}
问题
问题
当数组均为负数比如nums:[-2,-1],此代码会失效
maxCount只记录了count > 0时,当前连续子数组的最大值,但是忽略了数字仅包含负数的情况
针对当前count < 0时,也需要记录maxCount
错误代码
public int maxSubArray(int[] nums) {
int count = 0;// 连续子数组当前和
int maxCount = nums[0];// 连续子数组最大和
for (int i = 0; i < nums.length; i++) {
if (count + nums[i] < 0) {// 当前连续子数组总和为负数时,所以重新寻找子数组起始位置
count = 0;
} else {
count = count + nums[i];
if(count > maxCount) // 记录连续子数字最大和
maxCount = count;
}
}
return maxCount;
}
改进方式
public int maxSubArray(int[] nums) {
int count = 0;// 连续子数组当前和
int maxCount = Integer.MIN_VALUE;// 连续子数组最大和
for (int i = 0; i < nums.length; i++) {
count = count + nums[i];
if(count > maxCount) // 记录连续子数字最大和
maxCount = count;
if (count < 0) {// 当前连续子数组总和为负数时,所以重新寻找子数组起始位置
count = 0;
}
}
return maxCount;
}