初探字典树、Trie树 题目整理
字典树
字典树是一种处理前缀的数据结构
略懂数据结构的人,相信看完下面这张图就差不多理解了
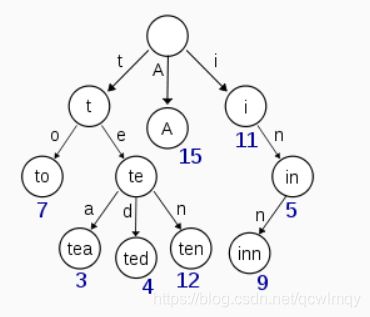
- T r i e Trie Trie的根节点是空的
(相信没有题目给的所有数据有公共前缀) - 每个节点储存一个单词/字母
- 根节点到每个单词节点的路径上的所有字母连接而成的字符串就是该节点对应的字符串
- 空间换时间的方法(1秒一般能解决的总字符数量在100000个,空间一般也开800000,适用于查询比较多的情况)
实现
以小写字母为例,讲解以下代码实现
节点
需要一个数组存储节点信息
外加一个mark标志,存储答案
struct Tree{
Tree() { //构造函数
mark = 0;
memset(son, 0, sizeof(son));
}
void clear() {
mark = 0;
memset(son, 0, sizeof(son));
}
int mark; //标记,一般为询问的值,视情况而定
int son[26]; //此处只考虑小写字母,即为节点存储的数据
}tree[maxn];
插入
逐层迭代,将没有的节点插入
在末尾节点的下一个节点存储该字符串的信息(因为由这个节点前面构成的字符串是唯一的)
int root, num; //根节点永久为0
void insert(char* str) {
int position = root; //初始化位置
for (int i = 0; str[i]; i++) {
int symbol = str[i] - 'a'; //转化函数,视情况而定
if (!tree[position].son[symbol])//创建新节点
tree[position].son[symbol] = ++num;
position = tree[position].son[symbol];
}
tree[position].mark++; //记录链末尾的数量
}
查询
逐层递归查找
int find(char* str) {
int position = root;
for (int i = 0; str[i]; i++) {
int symbol = str[i] - 'a';
if (!tree[position].son[symbol]) //找不到,返回false
return 0;
position = tree[position].son[symbol];//迭代寻找
}
return tree[position].mark; //返回相同链的数量
}
实际上,我们发现字典树是种很简单的数据结构,上面的插入和查询只是基本操作
当你理解上面的插入和查询操作后,也可以轻松实现其他操作
例题
P2580 于是他错误的点名开始了
题意
给出一组名字(好几个字符串)
进行m次点名,第一次字符串出现输出“OK”,第二次以上出现输出“REPEAT”,若该字符串不在给出字符串内输出“WRONG”
思路
板子题+1
mark记录该字符串是否出现过
记录该字符串被访问次数
P3879 [TJOI2010]阅读理解
题意
给出n组字符串,每组字符串有1个或多个字符串
有m组询问,询问为一个字符串,返回在哪几组字符串中出现过
思路
板子题+2
用vector存储一个字符串在哪几组字符串中出现过
P5149 会议座位
题意
按顺序给出 n n n个字符串
第一个字符串最小,第二个第二,以此类推
再次给出n个字符的顺序,求逆序对数
思路
板子题+3
字典树离散化字符串
归并排序求逆序对数
P3294 [SCOI2016]背单词
题意
给你n个字符串,不同的排列有不同的代价,代价按照如下方式计算(字符串s的位置为x)
1.排在s后面的字符串有s的后缀,则代价为n^2
2.排在s前面的字符串有s的后缀,且没有排在s后面的s的后缀,则代价为x-y(y为最后一个与s不相等的后缀的位置);
3.s没有后缀,则代价为x
求最小代价和
思路
显然第一种代价是不可能被用到的
只要按后缀逐个取字符就能避免第一种情况
处理后缀比较麻烦,我们将字符串翻转,就可以用字典树存储前缀
按前缀逐个取字符串
容易证明先取后缀少的字符串,最终代价少
先重构树,只保留存在的字符串
先 d f s dfs dfs处理各个子树的节点数
再根据子树权重,优先对权重小的子树搜索即可
//具体过程,类似树链剖分
例题代码
P2580 于是他错误的点名开始了
#include P3879 [TJOI2010]阅读理解
#include P5149 会议座位
#include P3294 [SCOI2016]背单词
#include