Java数据结构和算法——动态规划做题步骤详细总结

动态规划题目类型

1、计数：
有多少种方式走到右下角
有多少种方法选出k个数使得和为Sum
2、求最大最小值：
从左上角走到右下角路径的最大数字和
最长上升子序列长度
3、求存在性：
取石子游戏，先手是否必胜
能不能选出k个数使得和是Sum

动态规划解题步骤

1、确定状态
简单的说，就是解动态规划时需要开一个数组，数组的每个元素f[i]或者f[i][j]代表什么，类似解数学题中，xyz代表什么一样，具体分为下面两个步骤：
-------研究最优策略的最后一步
-------化为子问题
2、转移方程
根据子问题定义直接得到
3、初始条件和边界情况
初始条件一般都是a[0]、a[1]这种，多看看
边界条件主要是看数组的边界，数组越不越界
4、计算顺序
利用之前的计算结果

动态规划实例讲解

硬币问题

题目：有三种硬币，面值2.5.7，买一本书需要27元，如何用最少的硬币整好付清。

首先经过分析，这是一个求最大最小值问题，可用动态规划来求解。
1、确定状态
（1）最后一步
虽然我们不知道最优策略是什么，但是最优策略一定是k枚硬币a1,a2…ak加起来等于27
所以一定有一枚最后的硬币：ak
除掉这枚硬币，前面硬币的面值相加起来是27-ak，如图
（2）化为子问题
所以就将原问题转化为了子问题：
原问题是最少用多少枚硬币拼出27（k枚）
子问题是最少用多少枚硬币拼出27-ak（k-1枚）

经过这两歩，得出状态：f[X]=最少用多少枚硬币拼出X

2、转移方程
设状态f[X]=最少用多少枚硬币拼出X
转移方程如下
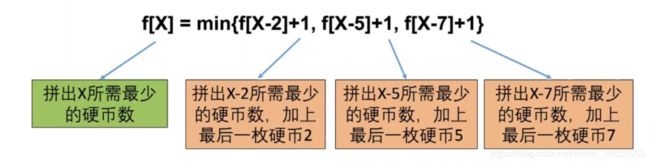这时，可以用递归进行解题，大致如下
但是有一个问题，递归是从上到下进行计算的，这样的话会产生大量的重复运算
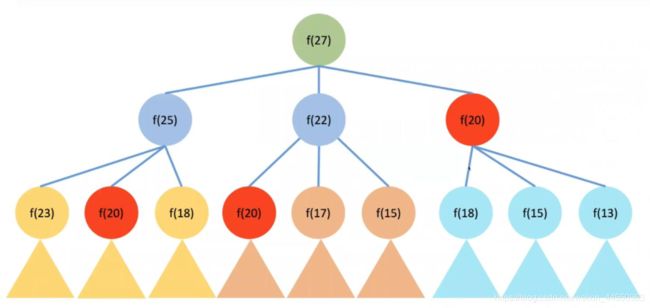所以说，这不是一个好的解法，解决方法就是将计算结果保存下来，改变计算顺序，我们接着来看。

3、初始条件和边界情况
边界条件X-2，X-5，X-7小于0时，应该进行处理，这种情况其实就是拼不出来的情况，定义为正无穷

初始条件一般就是根据转移方程计算不出来的值，从转移方程变量为0或1来选，根据题目进行分析，这个题目的初始条件就是f[0]=1，代入公式的话应该f[0]为正无穷，显然错误，所以自己定义f[0]=0

4、计算顺序
这个题目应该是正序的，当我们计算到f[X]时，f[X-2],f[X-5],f[X-7]都已经得到结果了

代码：

	//A数组存储硬币金额，M代表商品价值
	public static int coinChange(int[] A, int M) {
        int[] f = new int[M + 1];
        f[0] = 0;

        for (int i = 1; i <= M; i++) {
            f[i] = Integer.MAX_VALUE;
            for (int j = 0; j < A.length; j++) {
            	//第一个条件是防止数组越界；第二个条件是防止MAX_VALUE+1越界
                if (i >= A[j] && f[i - A[j]] != Integer.MAX_VALUE) {
                    f[i] = Math.min(f[i], f[i - A[j]] + 1);
                }
            }
        }

        if (f[M] == Integer.MAX_VALUE) {
            f[M] = -1;
        }

        return f[M];
    }

机器人路径问题

题目：给定m行n列的网格，有一个机器人从左上角（0,0）出发，每一步可以向下或者向右走一步，问有多少种不同的方式走到右下角。

可用计数型动态规划来求解。

1、确定状态
（1）最后一步
聚焦机器人最后挪动的一歩，右下角坐标为（m-1，n-1），那么前一步机器人一定在（m-2，n-1）或者（m-1，n-2）

（2）子问题
轻易可得，机器人走到（m-1，n-1）的方式等于机器人走到（m-2，n-1）加上机器人走到（m-1，n-2）
原问题是有多少种方式从左上角走到（m-1，n-1）
子问题是有多少种方式从左上角走到（m-2，n-1）和（m-1，n-2）

经过这两歩，得出状态：f[i][j]为机器人有多少种方式从左上角走到（i，j）

2、转移方程

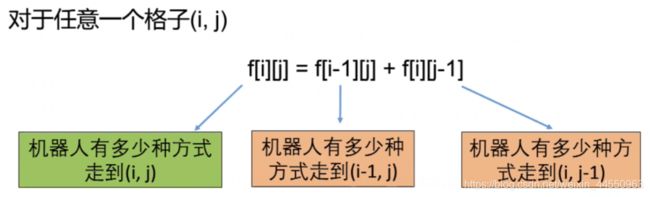
3、初始条件和边界情况
边界条件：i=0或者j=0时前一步只能从一个方向过来，所以f[i][j]=1

初始条件:f[0][0]=1，机器人只有一种方式到左上角

4、计算顺序
计算第0行
计算第1行
…
计算第m-1行

代码：

	public static int uniquePaths(int m, int n) {
        int[][] f = new int[m][n];
        int i, j;
        for (i = 0; i < m; i++) {
            for (j = 0; j < n; j++) {
                if (i == 0 || j == 0) {
                    f[i][j] = 1;
                } else {
                    f[i][j] = f[i - 1][j] + f[i][j - 1];
                }
            }
        }
        return f[m - 1][n - 1];
    }

青蛙跳石头问题

题目：有n块石头分别放在x轴的0,1，…，n-1位置，一只青蛙在石头0，想要跳到石头n-1，若青蛙在第i块石头上，他最多可以向右跳距离ai，问青蛙能否跳到石头n-1。

经过分析，这是一个存在型动态规划问题
1、确定状态
（1）最后一步
最后一步是从i跳过来的，i 需要满足两个条件：
青蛙可以跳到石头i；最后一步不能超过跳跃的最大距离，即n-1-i<=ai

（2）化为子问题
所以就将原问题转化为了子问题：
原问题是青蛙能不能跳到石头n-1
子问题是青蛙能不能跳到石头i

经过这两歩，得出状态：f[j]表示青蛙能不能跳到石头j

2、转移方程
f[j]表示青蛙能不能跳到石头j
转移方程如下

3、初始条件和边界情况
边界条件：枚举的i和j都不会越界，所以没有边界条件

初始条件:f[0]=true，因为青蛙一开始就在石头0上

4、计算顺序

代码：

	public static boolean canJump(int[] A) {
        boolean[] f = new boolean[A.length];
        f[0] = true;

        for (int j = 1; j < A.length; j++) {
            f[j] = false;
            for (int i = 0; i < j; i++) {
                if (f[i] && i + A[i] >= j) {
                    f[j] = true;
                    break;
                }
            }
        }
        return f[A.length - 1];
    }

剪绳子问题

题目：给你一根长度为n的绳子，请把绳子剪成整数长的m段（m、n都是整数，n>1并且m>1，m<=n），每段绳子的长度记为k[1],…,k[m]。请问k[1]x…xk[m]可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。（2 <= n <= 60）

可用最值型动态规划来求解。

1、确定状态
（1）最后一步
假设绳子剪得最后一下的长度为j，只需要满足j

（2）子问题
相当于从1开始遍历j，找出 j*（i-j部分的乘积最大值）的最大值
原问题是长度为i的乘积最大值
子问题是长度为i-j的乘积最大值

经过这两歩，得出状态：f[i]表示长度为i的绳子的乘积最大值

2、转移方程
f[i] = max( f[i] , j * f[i-j] )
f[i]初始值可以不动，设置为0
（其中要注意一个问题，这个式子f[i-j]会把绳子至少分为两段，但是当i-j < 4时, 不分割的情况下是最大的，（大于4就很明显不是了，比如5分为2和3，乘积大于5）显然back_track(n) = n，所以说这个i要从4开始，做子运算时i-j < 4时就按照i - j来计算）

3、初始条件和边界情况
边界条件：遍历自己控制不会越界，没有边界情况

初始条件:由于f[2],f[3]都要至少分为两段，结果不是2和3，而是1和2，所以要单独计算

4、计算顺序
从f[4]开始往后计算

代码：

	public int cutRope(int target) {
        if(target == 2){
            return 1;
        }else if(target == 3){
            return 2;
        }
        
        int[] f = new int[target+1];
        for(int i=1;i<=3;i++){
            f[i] = i;
        }
        for(int i=4;i<=target;i++){
            for(int j=1;j<i;j++){
                f[i] = Math.max(f[i],j*f[i-j]);
            }
        }
        
        return f[target];
    }

连续子数组的最大和

题目：HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组，返回它的最大连续子序列的和，你会不会被他忽悠住？(子向量的长度至少是1)

可用最值型动态规划来求解。

1、确定状态
（1）最后一步
假设当前要判断的是数组第i个，最后一步就是i，数组下标是i-1

（2）子问题
找出到第i-1个为止的连续子数组最大和，看其是否为正或为负，再判断
原问题是到数组第i个的连续子数组的最大和
子问题是到数组第i-1个的连续子数组的最大和

经过这两歩，得出状态：f[i]表示前i个元素的连续子数组的最大和，结尾元素为array[i-1]

2、转移方程
f[i] = max( array[i-1] , array[i-1] + f[i-1] )
如果当前元素为整数，并且f[i-1]为负数，那么当然结果就是只选当前元素，从当前元素开始计算子数组。这里有一个问题是这个方程算出来的连续子数组必须包含array[i-1]，所以说我们要用一个变量ret保存每一个f[i]，取一个最大的就是结果。

3、初始条件和边界情况
边界条件：遍历自己控制不会越界，没有边界情况

初始条件:f[0] = 0

4、计算顺序
从f[1]开始往后计算

代码：

public class Solution {
    public int FindGreatestSumOfSubArray(int[] array) {
        int[] f = new int[array.length + 1];
        f[0] = 0;
        int ret = array[0];
        for(int i=1;i<=array.length;i++){
            f[i] = Math.max(array[i-1],f[i-1] + array[i-1]);
            ret = Math.max(ret,f[i]);
        }
        return ret;
    }
}

最长不含重复字符的子字符串

题目：请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。

可用最值型动态规划来求解。

1、确定状态
（1）最后一步
假设当前要判断s[j]是否和前面的重复，最后一步就是s[j]

（2）子问题
原问题是最后一个字符为s[j]的不含重复字符的子字符串
原问题是最后一个字符为s[j-1]的不含重复字符的子字符串

经过这两歩，得出状态：f[j] 代表以字符 s[j] 为结尾的 “最长不重复子字符串” 的长度

2、转移方程
固定右边界 j ，设字符 s[j] 左边距离最近的相同字符为 s[i]，即 s[i] = s[j]

(1)当 i < 0，即 s[j]左边无相同字符，则 f[j] = f[j-1] + 1
(2)当 f[j - 1] < j - i，说明字符 s[i]在子字符串 f[j−1] 区间之外 ，则 f[j] = f[j - 1] + 1
(3)当 f[j−1] >= j−i ，说明字符 s[i] 在子字符串 f[j−1] 区间之中 ，则 f[j]的左边界由 s[i] 决定，即 f[j] = j − i
当 i < 0 时，由于 f[j−1] <= j 恒成立，因而 f[j−1] < j−i 恒成立，因此(1)/(2)可被合并

得到转移方程：
当f[j - 1] < j - i时，f[j] = f[j-1] + 1
当f[j - 1] >= j - i时，f[j] = j − i

3、初始条件和边界情况
边界条件：遍历自己控制不会越界，没有边界情况

初始条件:f[0] = 1

4、计算顺序
从f[1]开始往后计算

5、关键问题
观察转移方程，可知问题为：每轮遍历字符 s[j] 时，如何计算索引 i ？

可以用哈希表来解决
(1)哈希表统计： 遍历字符串 s 时，使用哈希表（记为 dic ）统计 各字符最后一次出现的索引位置
(2)左边界 i 获取方式： 遍历到 s[j] 时，可通过访问哈希表 ，dic[s[j]]获取最近的相同字符的索引 i，如果没有就默认为-1

代码：

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if(s.length() == 0){
            return 0;
        }
        Map<Character, Integer> dic = new HashMap<>();
        int[] f = new int[s.length()];
        f[0] = 1;
        dic.put(s.charAt(0),0);
        int res = 1;

        for(int j=1;j<s.length();j++){
            int i = dic.getOrDefault(s.charAt(j),-1);
            dic.put(s.charAt(j),j);
            if(j - i > f[j-1]){
                f[j] = f[j-1] + 1;
            }else{
                f[j] = j - i;
            }
            res = Math.max(f[j],res);
        }

        return res;
    }
}

6、空间优化
由于返回值是取 f 列表最大值，因此可借助变量 tmp 存储 f[j] ，变量 res 每轮更新最大值即可

此优化可节省 f 列表使用的 O(N) 大小的额外空间

代码：

class Solution {
    public int lengthOfLongestSubstring(String s) {
        Map<Character, Integer> dic = new HashMap<>();
        int res = 0, tmp = 0;
        for(int j = 0; j < s.length(); j++) {
            int i = dic.getOrDefault(s.charAt(j), -1); // 获取索引 i
            dic.put(s.charAt(j), j); // 更新哈希表
            tmp = tmp < j - i ? tmp + 1 : j - i; // dp[j - 1] -> dp[j]
            res = Math.max(res, tmp); // max(dp[j - 1], dp[j])
        }
        return res;
    }
}

最长回文子串

最长回文子串

看视频解析，第四步计算顺序很重要，画一个表格就很清晰了，先要算出左下值

最长上升子序列

最长上升子序列