牛客网TOP101刷题笔记汇总--C++题解
题目
- 链表
-
- BM1 反转链表
- BM2 链表内指定区间反转
- BM3 链表中的节点每k个一组翻转
- BM4 合并两个排序的链表
- BM5 合并k个已排序的链表
- BM6 判断链表中是否有环
- BM15 删除有序链表中重复的元素-I
- 二分查找/排序
- 二叉树
- 堆/栈/队列
- 哈希
- 递归/回溯
- 动态规划
- 字符串
- 双指针
- 贪心算法
- 模拟
链表
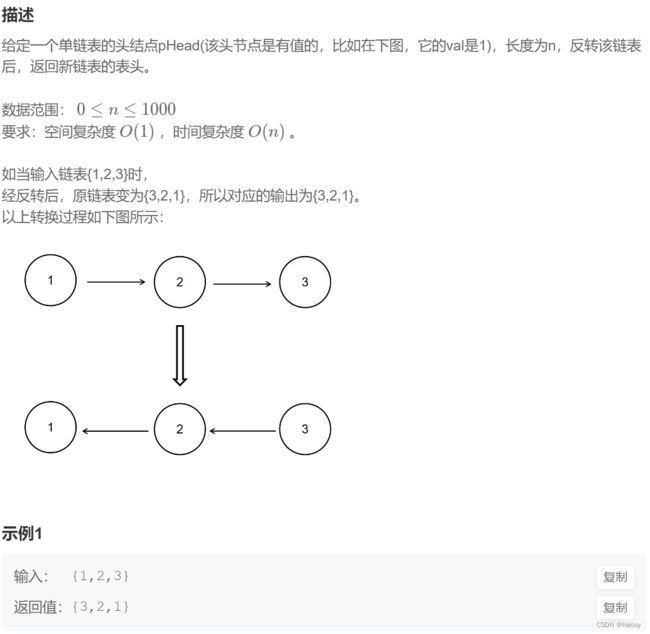
BM1 反转链表
分析1(通过调整链表指针达到反转):
初始化三个指针:pre、cur、next
next用来保存链表,防止cur改变指向后剩余链表失效
cur一开始指向头结点,pre置空
每次循环更新三个指针
next = cur->next; 保存作用
cur->next = pre; 指向反转
pre = cur, cur = next; 更新pre、cur的位置
直到cur走到nullptr时链表遍历完成,此时pre指向反转后的链表的头结点位置。返回pre
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类
* @return ListNode类
*/
ListNode* ReverseList(ListNode* head) {
// write code here
if(head == nullptr)
return nullptr;
ListNode* pre = nullptr;
ListNode* cur = head;
ListNode* next = nullptr;
while(cur != nullptr)
{
next = cur->next;
cur->next = pre;
pre = cur;
cur = next;
}
return pre;
}
};
分析2(使用vector容器反转函数):
将链表每个节点存入vector容器;
使用reverse函数进行反转
再将反转后的节点构造链表
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类
* @return ListNode类
*/
ListNode* ReverseList(ListNode* head) {
// write code here
if(head == nullptr)
return nullptr;
vector<ListNode*> v;
ListNode* cur = head;
while(cur != nullptr)
{
v.push_back(cur);
cur = cur->next;
}
//反转
reverse(v.begin(), v.end());
ListNode* reverseHead = v[0];
cur = reverseHead;
for(int i = 1; i < v.size(); ++i)
{
cur->next = v[i];
cur = cur->next;
}
cur->next = nullptr;
return reverseHead;
}
};
BM2 链表内指定区间反转
分析1(使用头插操作):
在链表前加一个表头,后续返回时去掉就好了,因为如果要从链表头的位置开始反转,在多了一个表头的情况下就能保证第一个节点永远不会反转,不会到后面去。
首先找到m(开始反转)的位置
然后开始执行头插操作,每次将cur的下一个位置元素进行头插,执行n-m次。
例如:将cur、next、nnext这三个元素反转
pre: cur next nnext
pre: next cur nnext
pre: nnext next cur
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类
* @param m int整型
* @param n int整型
* @return ListNode类
*/
ListNode* reverseBetween(ListNode* head, int m, int n) {
// write code here
if(!head)
return nullptr;
//加入表头
ListNode* res = new ListNode(-1);
res->next = head;
ListNode* pre = res;
ListNode* cur = head;
ListNode* next = nullptr;
//找到m位置
for(int i=1; i<m; ++i)
{
pre = cur;
cur = cur->next;
}
for(int i=m; i<n; i++)
{
//将next头插操作
// pre: cur next nnext
// pre: next cur nnext
// pre: nnext next cur
next = cur->next;
cur->next = next->next;
next->next = pre->next;
pre->next = next;
}
//返回去掉表头
return res->next;
}
};
分析2(使用vector区间反转):
将链表每个节点存入vector容器
使用reverse函数进行区间反转
再将反转后的节点构造链表
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类
* @param m int整型
* @param n int整型
* @return ListNode类
*/
ListNode* reverseBetween(ListNode* head, int m, int n) {
// write code here
if(!head)
return nullptr;
ListNode* cur = head;
vector<ListNode*> v;
while(cur != nullptr)
{
v.push_back(cur);
cur = cur->next;
}
reverse(v.begin()+m-1,v.begin()+n);
ListNode* reverseHead = v[0];
cur = reverseHead;
for(int i = 1; i < v.size(); ++i)
{
cur->next = v[i];
cur = cur->next;
}
cur->next = nullptr;
return reverseHead;
}
};
BM3 链表中的节点每k个一组翻转
分析(递归):
BM2的区间翻转部分头插代码正好可以用到这里
先把整个题目分解为多个小题目,即每k个一组翻转,分解后先实现每组内的翻转。
1.首先再链表前加一个表头,以便最后返回。
2.计算整个链表的节点个数,并通过节点个数整除k,求出翻转的次数。
3.写递归函数:
终止条件:翻转次数每次减1,为0时返回。
函数体:进行翻转并链接前后节点
继续递归,每次传入更新后的翻转起始节点的前一个节点,翻转起始节点,翻转区间,反转次数。
最终返回表头的next
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类
* @param k int整型
* @return ListNode类
*/
void reverseList(ListNode* pre, ListNode* cur, int k, int reverseNum)
{
if(reverseNum <= 0)
{
return;
}
else
{
for(int i = 1; i < k; i++)
{
//pre cur next nnext
//pre next cur nnext
ListNode* next = cur->next;
if(!next)
return;
cur->next = next->next;
next->next = pre->next;
pre->next = next;
}
--reverseNum;
reverseList(cur, cur->next, k, reverseNum);
}
}
ListNode* reverseKGroup(ListNode* head, int k) {
// write code here
//定义一个头结点
if(!head)
return nullptr;
ListNode* phead = new ListNode(-1);
phead->next = head;
//计算节点个数
int count = 1;
ListNode* cur = head;
while(cur != nullptr && cur->next != nullptr)
{
cur = cur->next;
++count;
}
//翻转次数
int reverseNum = count / k;
reverseList(phead, head, k, reverseNum);
return phead->next;
}
};
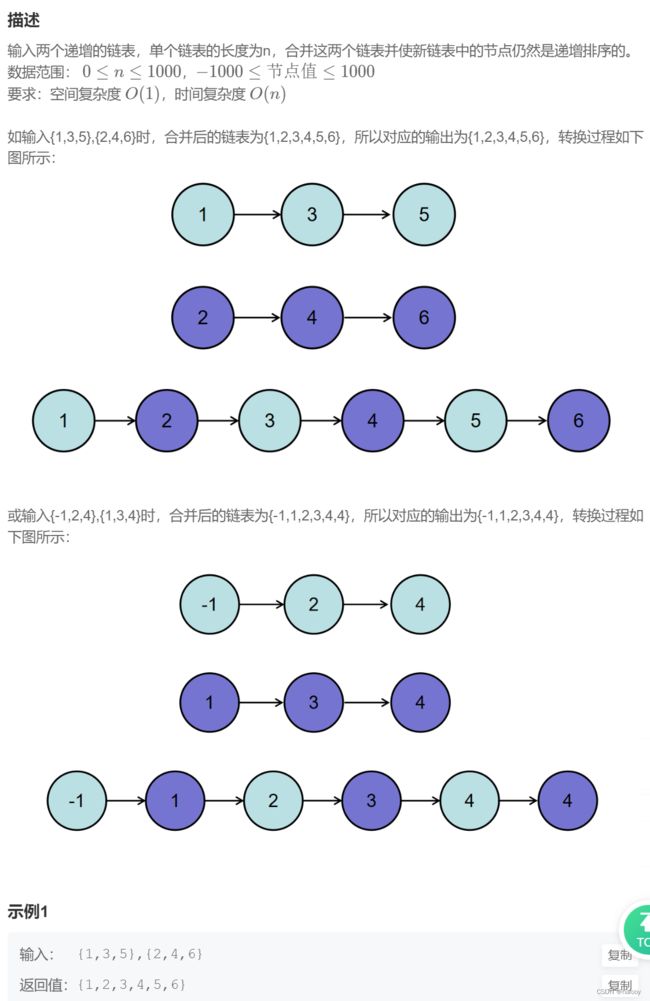
BM4 合并两个排序的链表
分析:
创建头结点,放置新链表之前,便于最后返回head->next,设置cur为当前节点,从head开始。
当两个链表都非空时,进入循环,比较两个链表的结点,更小的节点放入新链表,同时相应的新旧链表节点后移一位。
如果循环结束链表还有非空,则将非空链表剩余节点链接到新链表的后面。
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pHead1 ListNode类
* @param pHead2 ListNode类
* @return ListNode类
*/
ListNode* Merge(ListNode* pHead1, ListNode* pHead2) {
// write code here
//创建链表头结点便于最终返回
ListNode* head = new ListNode(-1);
ListNode* cur = head;
//当两个链表有一个其中为空时跳出循环
while(pHead1 && pHead2)
{
if(pHead1->val <= pHead2->val)
{
cur->next = pHead1;
cur = cur->next;
pHead1 = pHead1->next;
}
else
{
cur->next = pHead2;
cur = cur->next;
pHead2 = pHead2->next;
}
}
if(pHead1 == nullptr && pHead2 != nullptr)
{
cur->next = pHead2;
}
else if(pHead2 == nullptr && pHead1 != nullptr)
{
cur->next = pHead1;
}
return head->next;
}
};
BM5 合并k个已排序的链表
分析(归并分治思想):
将一个数组每次划分成等长的两部分,对两部分进行排序即是子问题。对子问题继续划分,直到子问题只有1个元素(每个元素即为一个链表)。还原的时候,将每个子问题和它相邻的另一个子问题利用之前排序方式,1个与1个合并成2个,2个与2个合并成4个,因为这每个单独的子问题合并好的都是有序的,直到合并成原本长度的数组。
终止条件: 划分的时候直到左右区间相等或左边大于右边。
返回值: 每级返回已经合并好的子问题链表。
本级任务: 对半划分,将划分后的子问题合并成新的链表。
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
#include
#include BM6 判断链表中是否有环
分析:
定义两个指针一开始都指向头节点,区别在于步长不同,一快一慢。
slow 指针每次向后移动一个位置,而fast 指针向后移动两个位置。如果链表中存在环,则 fast 指针最终将再次与 slow 指针在环中相遇。
如果不存在环,则fast指针会指向nullptr,则返回false
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
bool hasCycle(ListNode* head) {
if (head == nullptr) {
return false;
}
else
{
ListNode* fast;
ListNode* slow;
fast = slow = head;
while (fast != nullptr && fast->next != nullptr)
{
fast = fast->next->next;
slow = slow->next;
if(fast == slow)
{
return true;
}
}
return false;
}
}
};
BM15 删除有序链表中重复的元素-I
/**
* struct ListNode {
* int val;
* struct ListNode *next;
* ListNode(int x) : val(x), next(nullptr) {}
* };
*/
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param head ListNode类
* @return ListNode类
*/
ListNode* deleteDuplicates(ListNode* head) {
// write code here
if(head == nullptr)
return nullptr;
ListNode* cur = head;
while(cur != nullptr)
{
ListNode* next = cur->next;
//如果下一节点非空并且值与当前节点相同则去除
// cur next(删除) next->next
if(next != nullptr && cur->val == next->val)
{
cur->next = next->next;
}
//否则正常进行遍历
else
{
cur = cur->next;
}
}
return head;
}
};