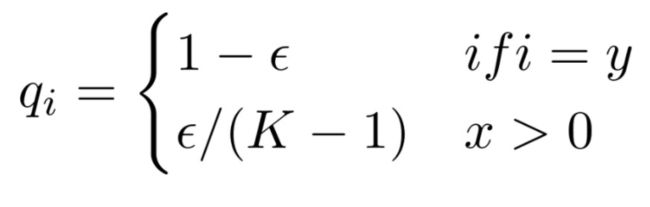Transformer代码实战
Transformer代码实战
翻译来自 http://nlp.seas.harvard.edu/2018/04/03/attention.html
在过去的一年里，很多人都想到了来自“Attention is All You Need”的 Transformer 。除了在翻译质量方面产生重大改进外，它还为许多其他 NLP 任务提供了一种新的架构。论文本身写得很清楚，但传统观点认为正确实施是相当困难的。
在这篇文章中，展示了这篇文章的注释版本。重新排序和删除了原始论文的一些部分，并添加了评论。总共有400行代码，在4个gpu上每秒可以处理27000个token。
首先需要安装Pytorch。 完整的notebook也可以在GitHub上或提供免费GPU的谷歌Colab上。
- Alexander Rush (@harvardnlp or [email protected])
下面是我个人依赖包版本
torchsummary==1.5.1
torchtext==0.9.0
tornado==6.1
scipy==1.7.0
seaborn==0.11.1
matplotlib==3.4.2
numpy==1.21.0
spacy==3.1.0
torch==1.8.0
# !pip install http://download.pytorch.org/whl/cu80/torch-0.3.0.post4-cp36-cp36m-linux_x86_64.whl numpy matplotlib spacy torchtext seaborn
来自两个任意输入或输出位置的信号所需的操作数量随着位置之间的距离而增加，对于 ConvS2S 是线性增长，对于 ByteNet 是对数增长。这使得学习远距离位置之间的依赖关系变得更加困难。在 Transformer 中，这被减少到恒定数量的操作，尽管代价是由于平均注意力加权位置而导致有效分辨率降低，我们使用多头注意力来抵消这种影响。
自注意，有时也称为内部注意，是一种将单个序列的不同位置关联起来以计算序列表示的注意机制。自注意力已成功用于各种任务，包括阅读理解、抽象摘要、原文意涵和学习与任务无关的句子表示。，Transformer 是第一个完全依赖自注意力来计算其输入和输出表示而不使用序列对齐的 RNN 或卷积的转换模型。
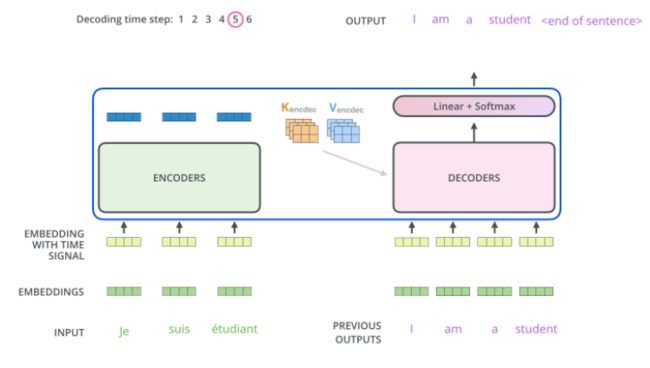
模型架构
大多数具有神经序列模型都具有编码器-解码器结构(cite)。在这里，编码器映射符号表示的输入序列 ( x 1 , . . . , x n ) (x_1, ..., x_n) (x1,...,xn)到一系列连续表示 z = ( z 1 , . . . , z n ) \mathbf{z} = (z_1, ..., z_n) z=(z1,...,zn)。给定 z \mathbf{z} z, 然后，解码器生成一个输出序列 ( y 1 , . . . , y m ) (y_1,...,y_m) (y1,...,ym)一次一个元素的符号。每一步模型都是自回归(cite), 在生成下一个符号时，使用之前生成的符号作为额外的输入。
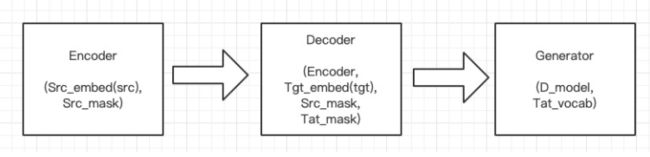
整体代码-Encode-Decoder
class EncoderDecoder(nn.Module):
"""
A standard Encoder-Decoder architecture. Base for this and many
other models.
"""
# super(EncoderDecoder, self).__init__() 等价于 nn.Module.__init__()
def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
super(EncoderDecoder, self).__init__()
self.encoder = encoder ## encoder 对象
self.decoder = decoder ## decoder 对象
self.src_embed = src_embed ## 字符编码
self.tgt_embed = tgt_embed ## 位置编码
self.generator = generator ## 最后输出层，线性层+softmax
# forward函数调用自身encode方法实现encoder，然后调用decode方式实现decoder
def forward(self, src, tgt, src_mask, tgt_mask):
#src的shape=tgt的shape：[batch_size,max_length]
"Take in and process masked src and target sequences."
return self.decode(self.encode(src, src_mask), src_mask,
tgt, tgt_mask)
def encode(self, src, src_mask):
return self.encoder(self.src_embed(src), src_mask)
def decode(self, memory, src_mask, tgt, tgt_mask):
return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)
class Generator(nn.Module):
"Define standard linear + softmax generation step."
def __init__(self, d_model, vocab):
super(Generator, self).__init__()
self.proj = nn.Linear(d_model, vocab)
def forward(self, x):
#nn.Linear是一个线性层，x*W
return F.log_softmax(self.proj(x), dim=-1)
Transformer 遵循这种整体架构，使用堆叠的自注意力和逐点、完全连接的编码器和解码器层。
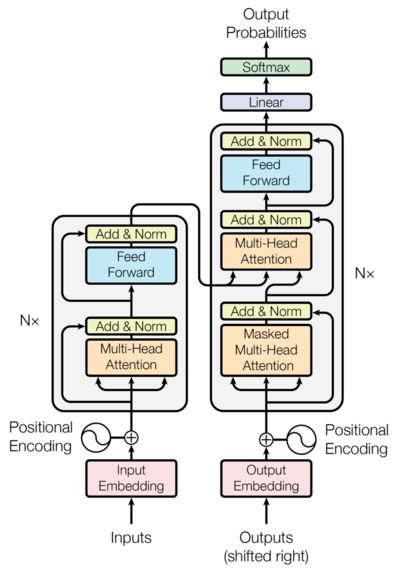
编码器和解码器block
编码器
编码器由6个相同block组成
def clones(module, N):
"Produce N identical layers."## 复制N层Block
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
class Encoder(nn.Module):
"Core encoder is a stack of N layers"
def __init__(self, layer, N):
super(Encoder, self).__init__()
self.layers = clones(layer, N) ## N层block
self.norm = LayerNorm(layer.size) ## 层归一化
def forward(self, x, mask):
"Pass the input (and mask) through each layer in turn."
for layer in self.layers:
x = layer(x, mask)
return self.norm(x)
我们在两个子层的每一个周围都使用了一个残差连接cite，然后是层归一化cite。
关于层归一化可以查看Transformer 与 Attention的一些Trick
class LayerNorm(nn.Module):
"Construct a layernorm module (See citation for details)."
def __init__(self, features, eps=1e-6):
super(LayerNorm, self).__init__()
self.a_2 = nn.Parameter(torch.ones(features))
self.b_2 = nn.Parameter(torch.zeros(features))
self.eps = eps ## 平滑系数
def forward(self, x):
mean = x.mean(-1, keepdim=True)
std = x.std(-1, keepdim=True)
return self.a_2 * (x - mean) / (std + self.eps) + self.b_2
即每个子层的输出为 L a y e r N o r m ( x + S u b l a y e r ( x ) ) \mathrm{LayerNorm}(x + \mathrm{Sublayer}(x)) LayerNorm(x+Sublayer(x)),其中 S u b l a y e r ( x ) \mathrm{Sublayer}(x) Sublayer(x)是由子层本身实现的函数。我们将 dropout cite应用于每个子层的输出，然后再将其添加到子层输入中并进行归一化。残差连接，模型中的所有子层以及嵌入层产生维度输出 d m o d e l = 512 d_{model}=512 dmodel=512
class SublayerConnection(nn.Module):
"""
A residual connection followed by a layer norm.
Note for code simplicity the norm is first as opposed to last.
"""
def __init__(self, size, dropout):
super(SublayerConnection, self).__init__()
self.norm = LayerNorm(size)
self.dropout = nn.Dropout(dropout)
def forward(self, x, sublayer):
"Apply residual connection to any sublayer with the same size."
return x + self.dropout(sublayer(self.norm(x)))
每层有两个子层。第一个是多头自注意力机制，第二个是简单的全连接前馈网络。
#传入参数
#EncoderLayer(d_model, c(attn), c(ff), dropout), N
class EncoderLayer(nn.Module):
"Encoder is made up of self-attn and feed forward (defined below)"
def __init__(self, size, self_attn, feed_forward, dropout):
super(EncoderLayer, self).__init__()
self.self_attn = self_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 2)
self.size = size
def forward(self, x, mask):
"Follow Figure 1 (left) for connections."
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
return self.sublayer[1](x, self.feed_forward)
解码
解码器也是由6个相同的block组成。
class Decoder(nn.Module):
"Generic N layer decoder with masking."
def __init__(self, layer, N):
super(Decoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, memory, src_mask, tgt_mask):
for layer in self.layers:
x = layer(x, memory, src_mask, tgt_mask)
return self.norm(x)
除了每个编码器层中的两个子层之外，解码器还插入了第三个子层，该子层对编码器stack的输出执行多头注意。与编码器类似，我们在每个子层周围使用残差连接，然后进行层归一化。
#传入参数
#DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N
class DecoderLayer(nn.Module):
"Decoder is made of self-attn, src-attn, and feed forward (defined below)"
def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
super(DecoderLayer, self).__init__()
self.size = size
self.self_attn = self_attn
self.src_attn = src_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 3)
# memory就是encoder完成之后的结果
def forward(self, x, memory, src_mask, tgt_mask):
"Follow Figure 1 (right) for connections."
m = memory
# self-attetion q=k=v,输入是decoder的embedding
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
# soft-attention q!=k=v x是deocder的embedding，m是encoder的输出
x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
return self.sublayer[2](x, self.feed_forward)
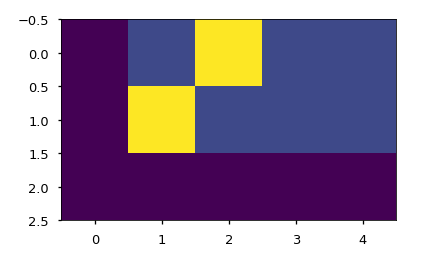
我们还修改了解码器stack中的自注意力子层，以防止位置关注后续位置。这种掩蔽与输出嵌入偏移一个位置的事实相结合，确保了位置的预测 i i i只能依赖小于位置的已知输出 i i i .
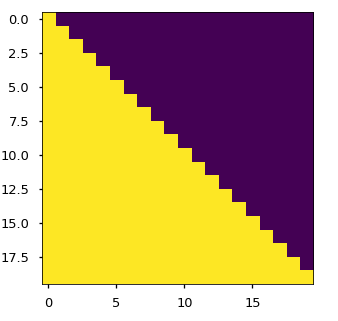
def subsequent_mask(size):
"Mask out subsequent positions."
attn_shape = (1, size, size)
subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
# print(subsequent_mask)
return torch.from_numpy(subsequent_mask) == 0
注意掩码下面显示了每个tgt单词(行)允许查看的位置(列)。
plt.figure(figsize=(5,5))
plt.imshow(subsequent_mask(20)[0])
None
注意力
注意力函数可以描述为将query和key-value pairs映射到一个输出，其中query, keys, values和输出都是向量。输出计算为值的加权总和，其中分配给每个值的权重由query与相应key函数计算。
我们将我们的特别关注称为“Scaled Dot-Product Attention“。输入由维度为 d k d_k dk query和keys ，和维度为 d v d_v dv values. 我们使用所有keys 计算查询的点积，将每个键除以 d k \sqrt{d_k} dk，并应用 softmax 函数来获得值的权重。
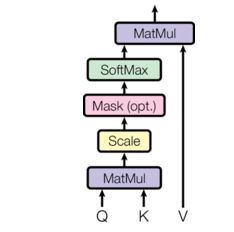
在实践中，我们同时计算一组queries的注意力函数，以一个矩阵 Q Q Q . keys和values也被以矩阵 K K K 和 V V V . 我们计算输出矩阵为：
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V \mathrm{Attention}(Q, K, V) = \mathrm{softmax}(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dkQKT)V
def attention(query, key, value, mask=None, dropout=None):
# shape:query=key=value---->[batch_size,8,max_length,64]
d_k = query.size(-1)
# k的纬度交换后为：[batch_size,8,64,max_length]
# scores的纬度为:[batch_size,8,max_length,max_length]
scores = torch.matmul(query, key.transpose(-2, -1)) \
/ math.sqrt(d_k)
#padding mask
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = F.softmax(scores, dim = -1)
if dropout is not None:
p_attn = dropout(p_attn)
return torch.matmul(p_attn, value), p_attn
最常用的两个注意函数是相加注意力cite和点积注意力(乘法)。点积注意力与我们的算法相同，除了比例因子 1 d k \frac{1}{\sqrt{d_k}} dk1。注意力使用具有单一隐含层的前馈网络计算函数。虽然两者在理论上的复杂性相似，但点积注意力在实践中要快得多，空间效率更高，因为它可以使用高度优化的矩阵乘法代码来实现。
而对于较小 d k d_k dk值两种机制表现相似，没有缩放更大 d k d_k dk值加性注意力表现优于点积注意力cite。我们怀疑,对于大的 d k d_k dk值,点积增大,迫使将softmax函数有非常小的梯度(为了说明为什么点积变大,假设q和k的组件是独立的随机变量均值为0,方差为1，然后它们的点积 q ⋅ k = ∑ i = 1 d k q i k i q \cdot k = \sum_{i=1}^{d_k} q_ik_i q⋅k=∑i=1dkqiki有均值0，方差1）
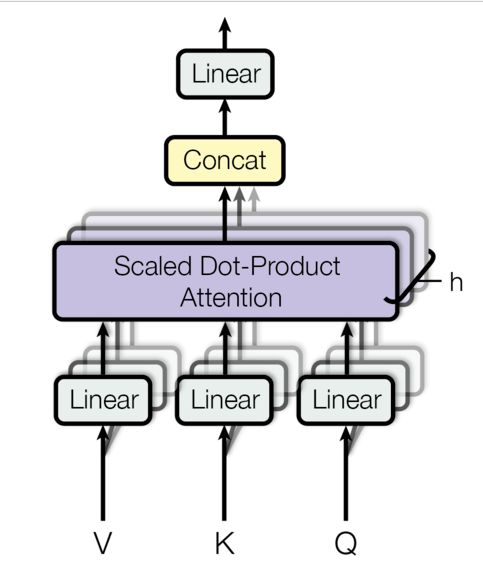
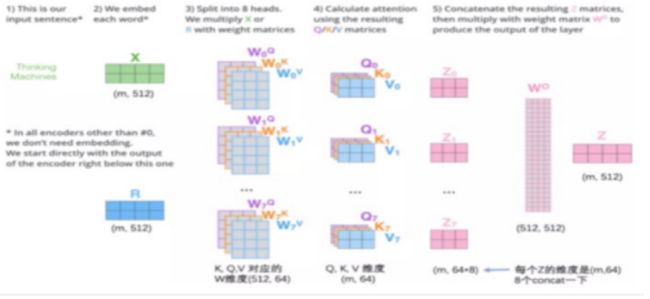
多头注意允许模型共同关注来自不同位置的不同表示子空间的信息。
M u l t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , . . . , h e a d h ) W O where h e a d i = A t t e n t i o n ( Q W i Q , K W i K , V W i V ) \mathrm{MultiHead}(Q, K, V) = \mathrm{Concat}(\mathrm{head_1}, ..., \mathrm{head_h})W^O \\ \text{where}~\mathrm{head_i} = \mathrm{Attention}(QW^Q_i, KW^K_i, VW^V_i) MultiHead(Q,K,V)=Concat(head1,...,headh)WOwhere headi=Attention(QWiQ,KWiK,VWiV)
其中投影是参数矩阵 W i Q ∈ R d model × d k W^Q_i \in \mathbb{R}^{d_{\text{model}} \times d_k} WiQ∈Rdmodel×dk, W i K ∈ R d model × d k W^K_i \in \mathbb{R}^{d_{\text{model}} \times d_k} WiK∈Rdmodel×dk, W i V ∈ R d model × d v W^V_i \in \mathbb{R}^{d_{\text{model}} \times d_v} WiV∈Rdmodel×dv和 W O ∈ R h d v × d model W^O \in \mathbb{R}^{hd_v \times d_{\text{model}}} WO∈Rhdv×dmodel
在这项工作中，我们使用了 h = 8 h=8 h=8平行的注意力层，或head。对于每一个我们使用的 d k = d v = d model / h = 64 d_k=d_v=d_{\text{model}}/h=64 dk=dv=dmodel/h=64由于每个head的尺寸减小，总的计算代价与全维单头注意力相似。
class MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model, dropout=0.1):
"Take in model size and number of heads."
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0
# We assume d_v always equals d_k
self.d_k = d_model // h
self.h = h
self.linears = clones(nn.Linear(d_model, d_model), 4)
self.attn = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
# 纬度
# shape:query=key=value--->:[batch_size,max_legnth,embedding_dim=512]
if mask is not None:
# Same mask applied to all h heads.
mask = mask.unsqueeze(1)
nbatches = query.size(0)
#第一步：将q,k,v分别与Wq，Wk，Wv矩阵进行相乘
#shape:Wq=Wk=Wv----->[512,512]
#第二步：将获得的Q、K、V在第三个纬度上进行切分
#shape:[batch_size,max_length,8,64]
#第三部：填充到第一个纬度
#shape:[batch_size,8,max_length,64]
query, key, value = \
[l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linears, (query, key, value))]
#进入到attention之后纬度不变，shape:[batch_size,8,max_length,64]
x, self.attn = attention(query, key, value, mask=mask,
dropout=self.dropout)
# 将纬度进行还原
# 交换纬度：[batch_size,max_length,8,64]
# 纬度还原：[batch_size,max_length,512]
x = x.transpose(1, 2).contiguous() \
.view(nbatches, -1, self.h * self.d_k)
# 最后与WO大矩阵相乘 shape:[512,512]
return self.linears[-1](x)
注意力在模型中的应用
Transformer 以三种不同的方式使用多头注意力：
- 在“编码器-解码器注意力”层中，queries来自前一个解码器层，记忆keys和values来自编码器的输出。这允许解码器中的每个位置都参与输入序列中的所有位置。这模仿了序列到序列模型（例如cite ）中典型的编码器-解码器注意力机制。
- 编码器包含自注意力层。在自注意力层中，所有的keys、values和queries都来自同一个地方，在这种情况下，是编码器上一层的输出。编码器中的每个位置都可以参与编码器前一层中的所有位置。
- 类似地，解码器中的自注意力层允许解码器中的每个位置关注解码器中直到并包括该位置的所有位置。我们需要防止解码器中的左向信息流出以保留自回归特性。我们通过屏蔽（设置为 − ∞ − ∞ −∞ ) softmax 输入中与非法连接相对应的所有值。
Position-wise前馈网络
除了注意力子层之外，我们编码器和解码器中的每一层都包含一个完全连接的前馈网络，它分别且相同地应用于每个位置。这包括两个线性变换，其间有一个ReLU激活。
F F N ( x ) = max ( 0 , x W 1 + b 1 ) W 2 + b 2 \mathrm{FFN}(x)=\max(0, xW_1 + b_1) W_2 + b_2 FFN(x)=max(0,xW1+b1)W2+b2
虽然不同位置的线性变换是相同的，但它们在层与层之间使用不同的参数。另一种描述方式是内核大小为 1 的两个卷积。输入和输出的维度是 d m o d e l = 512 d_{model}=512 dmodel=512,并且内层具有维度 d f f = 2048 d_{ff}=2048 dff=2048
class PositionwiseFeedForward(nn.Module):
"Implements FFN equation."
def __init__(self, d_model, d_ff, dropout=0.1):
super(PositionwiseFeedForward, self).__init__()
self.w_1 = nn.Linear(d_model, d_ff)
self.w_2 = nn.Linear(d_ff, d_model)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
return self.w_2(self.dropout(F.relu(self.w_1(x))))
Embeddings 和 Softmax
与其他序列转导模型类似，学习Embedding将输入标记和输出标记转换为维度向量 d model d_{\text{model}} dmodel模型 . 我们还使用通常学习的线性变换和 softmax 函数将解码器输出转换为预测的下一个标记概率。在我们的模型中，我们在两个嵌入层和 pre-softmax 线性变换之间共享相同的权重矩阵，类似于cite。在嵌入层中，我们将这些权重乘以 d model \sqrt{d_{\text{model}}} dmodel
class Embeddings(nn.Module):
def __init__(self, d_model, vocab):
super(Embeddings, self).__init__()
self.lut = nn.Embedding(vocab, d_model)
self.d_model = d_model
def forward(self, x):
return self.lut(x) * math.sqrt(self.d_model)
位置编码
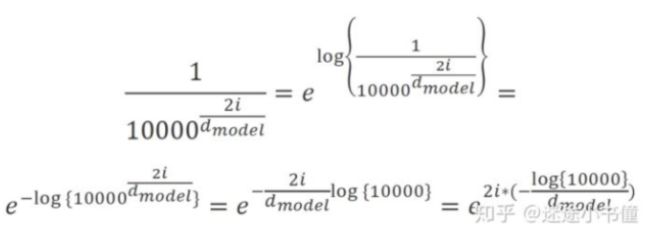
由于我们的模型不包含递归和卷积，为了让模型利用序列的顺序，我们必须注入一些关于标记在序列中的相对或绝对位置的信息。为此，我们将“位置编码”添加到编码器和解码器堆栈底部的输入嵌入中。位置编码具有相同的维度 d m o d e l d_{model} dmodel作为嵌入，因此可以将两者相加。位置编码有多种选择cite,我们使用不同频率的正弦和余弦函数：
P E ( p o s , 2 i ) = s i n ( p o s / 1000 0 2 i / d model ) PE_{(pos,2i)} = sin(pos / 10000^{2i/d_{\text{model}}}) PE(pos,2i)=sin(pos/100002i/dmodel)
P E ( p o s , 2 i + 1 ) = c o s ( p o s / 1000 0 2 i / d model ) PE_{(pos,2i+1)} = cos(pos / 10000^{2i/d_{\text{model}}}) PE(pos,2i+1)=cos(pos/100002i/dmodel)
其中 p o s pos pos是位置， i i i是维度。也就是说，位置编码的每个维度对应一个正弦曲线。波长形成几何级数，从 2 π 2 \pi 2π至 100002 π 10000 2 \pi 100002π,选择这个函数是因为我们假设它可以让模型很容易地学会通过相对位置来参与，因为对于任何固定的偏移量 k k k, P E p o s + k PE_{pos+k} PEpos+k可以表示为线性函数 P E p o s PE_{pos} PEpos.
此外，我们将 dropout 应用于编码器和解码器stack中的嵌入和位置编码的总和。对于基本模型，我们使用的比率为 P d r o p = 0.1 P_{drop}=0.1 Pdrop=0.1.
# print(torch.arange(0,5).unsqueeze(1))
# print(torch.arange(0,4,2))
class PositionalEncoding(nn.Module):
"Implement the PE function."
def __init__(self, d_model, dropout, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
# Compute the positional encodings once in log space.
pe = torch.zeros(max_len, d_model)
position = torch.arange(0., max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0., d_model, 2) *
-(math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, x):
x = x + Variable(self.pe[:, :x.size(1)],
requires_grad=False)
return self.dropout(x)
下面的位置编码将根据位置添加正弦波。波的频率和偏移对于每个维度都是不同的。
plt.figure(figsize=(15, 5))
pe = PositionalEncoding(20, 0)
y = pe.forward(Variable(torch.zeros(1, 100, 20)))
plt.plot(np.arange(100), y[0, :, 4:8].data.numpy())
plt.legend(["dim %d"%p for p in [4,5,6,7]])
None
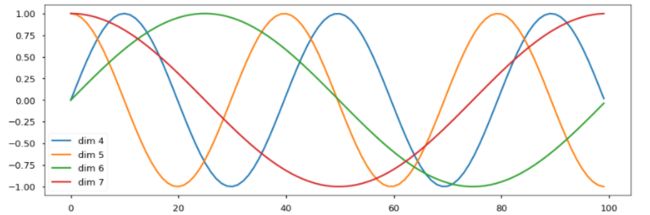
尝试使用学习的位置嵌入cite代替，发现两个版本产生了几乎相同的结果。我们选择了正弦版本，因为它可能允许模型外推到比训练期间遇到的序列长度更长的序列长度。
完整模型
在这里，我们定义了一个从超参数到完整模型的函数。
import copy
def make_model(src_vocab, tgt_vocab, N=6,
d_model=512, d_ff=2048, h=8, dropout=0.1):
"Helper: Construct a model from hyperparameters."
c = copy.deepcopy
attn = MultiHeadedAttention(h, d_model)
ff = PositionwiseFeedForward(d_model, d_ff, dropout)
position = PositionalEncoding(d_model, dropout)
model = EncoderDecoder(
Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
Decoder(DecoderLayer(d_model, c(attn), c(attn),
c(ff), dropout), N),
nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
Generator(d_model, tgt_vocab))
# This was important from their code.
# Initialize parameters with Glorot / fan_avg.
for p in model.parameters():
if p.dim() > 1:
nn.init.xavier_uniform(p)
return model
# Small example model.
tmp_model = make_model(10, 10, 2)
None
训练
我们停下来快速介绍一些训练标准编码器解码器模型所需的工具。首先，我们定义一个批处理对象，其中包含用于训练的 src 和目标句子，以及构建掩码。
Batches 和 Masking
class Batch:
"Object for holding a batch of data with mask during training."
def __init__(self, src, trg=None, pad=0):
self.src = src
self.src_mask = (src != pad).unsqueeze(-2)
if trg is not None:
self.trg = trg[:, :-1]
self.trg_y = trg[:, 1:]
self.trg_mask = \
self.make_std_mask(self.trg, pad)
self.ntokens = (self.trg_y != pad).data.sum()
@staticmethod
def make_std_mask(tgt, pad):
"Create a mask to hide padding and future words."
tgt_mask = (tgt != pad).unsqueeze(-2)
tgt_mask = tgt_mask & Variable(
subsequent_mask(tgt.size(-1)).type_as(tgt_mask.data))
return tgt_mask
接下来我们创建一个通用的训练和评分函数来跟踪损失。我们传入一个通用的损失计算函数，它也处理参数更新。
Training Loop
def run_epoch(data_iter, model, loss_compute):
"Standard Training and Logging Function"
start = time.time()
total_tokens = 0
total_loss = 0
tokens = 0
for i, batch in enumerate(data_iter):
out = model.forward(batch.src, batch.trg,
batch.src_mask, batch.trg_mask)
loss = loss_compute(out, batch.trg_y, batch.ntokens)
total_loss += loss
total_tokens += batch.ntokens
tokens += batch.ntokens
if i % 50 == 1:
elapsed = time.time() - start
print("Epoch Step: %d Loss: %f Tokens per Sec: %f" %
(i, loss / batch.ntokens, tokens / elapsed))
start = time.time()
tokens = 0
return total_loss / total_tokens
Training Data 和 Batching
我们在包含约 450 万个句子对的标准 WMT 2014 英德数据集上进行了训练。句子使用字节对编码进行编码，它具有大约 37000 个标记的共享源-目标词汇表。对于英法，我们使用了明显更大的 WMT 2014 英法数据集，该数据集由 3600 万个句子组成，并将标记拆分为 32000 个单词词表。
句子对按近似序列长度分批在一起。每个训练批次包含一组句子对，其中包含大约 25000 个源标记和 25000 个目标标记。
global max_src_in_batch, max_tgt_in_batch
def batch_size_fn(new, count, sofar):
"Keep augmenting batch and calculate total number of tokens + padding."
global max_src_in_batch, max_tgt_in_batch
if count == 1:
max_src_in_batch = 0
max_tgt_in_batch = 0
max_src_in_batch = max(max_src_in_batch, len(new.src))
max_tgt_in_batch = max(max_tgt_in_batch, len(new.trg) + 2)
src_elements = count * max_src_in_batch
tgt_elements = count * max_tgt_in_batch
return max(src_elements, tgt_elements)
Hardware 和 Schedule
我们在一台配备 8 个 NVIDIA P100 GPU 的机器上训练我们的模型。对于我们使用整篇论文中描述的超参数的基本模型，每个训练步骤大约需要 0.4 秒。我们对基本模型进行了总共 100,000 步或 12 小时的训练。对于我们的大型模型，步骤时间为 1.0 秒。大模型训练了 300,000 步（3.5 天）。
优化器
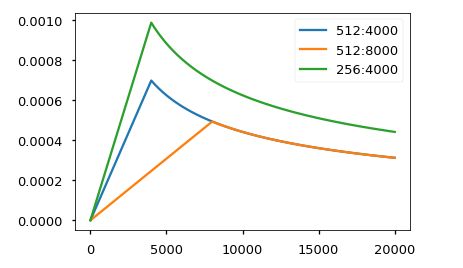
我们用Adam优化器cite, β 1 = 0.9 , β 2 = 0.98 \beta_1=0.9, \beta_2=0.98 β1=0.9,β2=0.98和 ϵ = 1 0 − 9 \epsilon=10^{-9} ϵ=10−9,我们根据以下公式在训练过程中改变学习率: l r a t e = d model − 0.5 ⋅ min ( s t e p _ n u m − 0.5 , s t e p _ n u m ⋅ w a r m u p _ s t e p s − 1.5 ) lrate = d_{\text{model}}^{-0.5} \cdot \min({step\_num}^{-0.5}, {step\_num} \cdot {warmup\_steps}^{-1.5}) lrate=dmodel−0.5⋅min(step_num−0.5,step_num⋅warmup_steps−1.5) 这对应于第一个线性增加学习率 w a r m u p s t e p s warmup_steps warmupsteps训练步数，然后与步数的平方根成反比地减少它。我们用了 w a r m u p _ s t e p s = 4000 warmup\_steps=4000 warmup_steps=4000
class NoamOpt:
"Optim wrapper that implements rate."
def __init__(self, model_size, factor, warmup, optimizer):
self.optimizer = optimizer
self._step = 0
self.warmup = warmup
self.factor = factor
self.model_size = model_size
self._rate = 0
def step(self):
"Update parameters and rate"
self._step += 1
rate = self.rate()
for p in self.optimizer.param_groups:
p['lr'] = rate
self._rate = rate
self.optimizer.step()
def rate(self, step = None):
"Implement `lrate` above"
if step is None:
step = self._step
return self.factor * \
(self.model_size ** (-0.5) *
min(step ** (-0.5), step * self.warmup ** (-1.5)))
def get_std_opt(model):
return NoamOpt(model.src_embed[0].d_model, 2, 4000,
torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))
此模型针对不同模型大小和优化超参数的曲线示例。
# Three settings of the lrate hyperparameters.
opts = [NoamOpt(512, 1, 4000, None),
NoamOpt(512, 1, 8000, None),
NoamOpt(256, 1, 4000, None)]
plt.plot(np.arange(1, 20000), [[opt.rate(i) for opt in opts] for i in range(1, 20000)])
plt.legend(["512:4000", "512:8000", "256:4000"])
None
正则化
标签平滑
在训练期间，我们使用了值的标签平滑值 ϵ l s = 0.1 \epsilon_{ls}=0.1 ϵls=0.1这会降低困惑度，因为模型会变得更加不确定，但会提高准确性和 BLEU 分数。
我们使用 KL div 损失实现标签平滑。我们没有使用 one-hot 目标分布，而是创建了一个分布，该分布具有confidence正确的单词和smoothing分布在整个词汇表中的其余质量。
class LabelSmoothing(nn.Module):
"Implement label smoothing."
def __init__(self, size, padding_idx, smoothing=0.0):
super(LabelSmoothing, self).__init__()
self.criterion = nn.KLDivLoss(size_average=False)
self.padding_idx = padding_idx
self.confidence = 1.0 - smoothing
self.smoothing = smoothing
self.size = size
self.true_dist = None
def forward(self, x, target):
#x====>[batch_size*max_length-1,vocab_size]
#target====>[batch_size*max_length-1]
assert x.size(1) == self.size
true_dist = x.data.clone()
#fill_就是填充
true_dist.fill_(self.smoothing / (self.size - 2))
#scatter_修改元素
true_dist.scatter_(1, target.data.unsqueeze(1), self.confidence)
true_dist[:, self.padding_idx] = 0
mask = torch.nonzero(target.data == self.padding_idx)
if mask.dim() > 0:
true_dist.index_fill_(0, mask.squeeze(), 0.0)
self.true_dist = true_dist
return self.criterion(x, Variable(true_dist, requires_grad=False))
在这里，我们可以看到一个示例，说明质量如何根据置信度分配给单词。
# Example of label smoothing.
crit = LabelSmoothing(5, 0, 0.4)
predict = torch.FloatTensor([[0, 0.2, 0.7, 0.1, 0],
[0, 0.2, 0.7, 0.1, 0],
[0, 0.2, 0.7, 0.1, 0]])
v = crit(Variable(predict.log()),
Variable(torch.LongTensor([2, 1, 0])))
# Show the target distributions expected by the system.
plt.imshow(crit.true_dist)
None
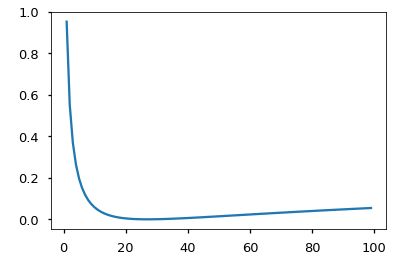
如果模型对给定的选择非常有信心，标签平滑实际上会开始惩罚模型。
crit = LabelSmoothing(5, 0, 0.1)
def loss(x):
d = x + 3 * 1
predict = torch.FloatTensor([[0, x / d, 1 / d, 1 / d, 1 / d],
])
#print(predict)
return crit(Variable(predict.log()),
Variable(torch.LongTensor([1]))).data.item()
plt.plot(np.arange(1, 100), [loss(x) for x in range(1, 100)])
# None
第一个例子
生成数据
def data_gen(V, batch, nbatches):
"Generate random data for a src-tgt copy task."
for i in range(nbatches):
data = torch.from_numpy(np.random.randint(1, V, size=(batch, 10)))
data[:, 0] = 1
src = Variable(data, requires_grad=False).long()
tgt = Variable(data, requires_grad=False).long()
yield Batch(src, tgt, 0)
损失计算
class SimpleLossCompute:
"A simple loss compute and train function."
def __init__(self, generator, criterion, opt=None):
self.generator = generator
#criterion 为LabelSmoothing方法
self.criterion = criterion
self.opt = opt
def __call__(self, x, y, norm):
#x对对应于out，也就是预测的时刻[batch_size,max_length-1,vocab_size]
#y对应于trg_y,也就是t时刻 [batch_size,max_length-1]
x = self.generator(x)
#x.contiguous().view(-1, x.size(-1)) ====>[batch_size*max_length-1,vocab_size]
#y.contiguous().view(-1)=========>[batch_size*max_length-1]
loss = self.criterion(x.contiguous().view(-1, x.size(-1)),
y.contiguous().view(-1)) / norm
loss.backward()
if self.opt is not None:
self.opt.step()
self.opt.optimizer.zero_grad()
return loss.data.item() * norm
Greedy解码
# Train the simple copy task.
V = 11
criterion = LabelSmoothing(size=V, padding_idx=0, smoothing=0.0)
model = make_model(V, V, N=2)
model_opt = NoamOpt(model.src_embed[0].d_model, 1, 400,
torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))
for epoch in range(10):
model.train()
run_epoch(data_gen(V, 30, 20), model,
SimpleLossCompute(model.generator, criterion, model_opt))
model.eval()
print(run_epoch(data_gen(V, 30, 5), model,
SimpleLossCompute(model.generator, criterion, None)))
为了简单，此代码使用贪婪解码来预测翻译。
def greedy_decode(model, src, src_mask, max_len, start_symbol):
memory = model.encode(src, src_mask)
#ys是decode的时候起始标志
ys = torch.ones(1, 1).fill_(start_symbol).type_as(src.data)
print(ys)
for i in range(max_len-1):
out = model.decode(memory, src_mask,
Variable(ys),
Variable(subsequent_mask(ys.size(1))
.type_as(src.data)))
prob = model.generator(out[:, -1])
_, next_word = torch.max(prob, dim = 1)
next_word= next_word.data[0]
ys = torch.cat([ys,
torch.ones(1, 1).type_as(src.data).fill_(next_word)], dim=1)
print("ys:"+str(ys))
return ys
model.eval()
src = Variable(torch.LongTensor([[1,2,3,4,5,6,7,8,9,10]]) )
src_mask = Variable(torch.ones(1, 1, 10) )
# print("ys:"+str(ys))
print(greedy_decode(model, src, src_mask, max_len=10, start_symbol=1))
真实示例
现在我们考虑一个使用 IWSLT 德语-英语翻译任务的真实示例。这个任务比论文中考虑的 WMT 任务小得多，但它说明了整个系统。我们还展示了如何使用多 GPU 处理使其真正快速。
#!pip install torchtext spacy
#!python -m spacy download en_core_web_sm
#!python -m spacy download de_core_news_sm
# For data loading.
from torchtext.legacy import data, datasets
from torchtext.legacy.data import Field
if True:
import spacy
spacy_de = spacy.load('de_core_news_sm')
spacy_en = spacy.load('en_core_web_sm')
def tokenize_de(text):
return [tok.text for tok in spacy_de.tokenizer(text)]
def tokenize_en(text):
return [tok.text for tok in spacy_en.tokenizer(text)]
BOS_WORD = ''
EOS_WORD = ''
BLANK_WORD = ""
SRC = Field(tokenize=tokenize_de, pad_token=BLANK_WORD)
TGT = Field(tokenize=tokenize_en, init_token = BOS_WORD,
eos_token = EOS_WORD, pad_token=BLANK_WORD)
MAX_LEN = 100
train, val, test = datasets.IWSLT.splits(
exts=('.de', '.en'), fields=(SRC, TGT),
filter_pred=lambda x: len(vars(x)['src']) <= MAX_LEN and
len(vars(x)['trg']) <= MAX_LEN)
MIN_FREQ = 2
SRC.build_vocab(train.src, min_freq=MIN_FREQ)
TGT.build_vocab(train.trg, min_freq=MIN_FREQ)
批处理对速度非常重要。我们希望有非常均匀的批次，绝对最小的填充。为此，我们必须对默认的 torchtext 批处理进行一些修改。此代码修补了它们的默认批处理，以确保我们搜索足够的句子以找到批处理。
迭代器
class MyIterator(data.Iterator):
def create_batches(self):
if self.train:
def pool(d, random_shuffler):
for p in data.batch(d, self.batch_size * 100):
p_batch = data.batch(
sorted(p, key=self.sort_key),
self.batch_size, self.batch_size_fn)
for b in random_shuffler(list(p_batch)):
yield b
self.batches = pool(self.data(), self.random_shuffler)
else:
self.batches = []
for b in data.batch(self.data(), self.batch_size,
self.batch_size_fn):
self.batches.append(sorted(b, key=self.sort_key))
def rebatch(pad_idx, batch):
"Fix order in torchtext to match ours"
src, trg = batch.src.transpose(0, 1), batch.trg.transpose(0, 1)
return Batch(src, trg, pad_idx)
多 GPU 训练
最后，为了真正针对快速训练，我们将使用多 GPU。此代码实现了多 GPU 单词生成。它不是特定于Transformer的，所以我不会详细介绍。这个想法是在训练时将单词生成分成多个块，以便在许多不同的 GPU 上并行处理。我们使用 pytorch 并行来做到这一点：
- replicate - 将模块拆分到不同的 GPU 上。
- scatter - 将批次拆分到不同的 GPU 上
- parallel_apply -将模块应用于不同 GPU 上的批次
- gather - 将分散的数据拉回到一个 GPU 上。
- nn.DataParallel - 一个特殊的模块包装器，在评估之前调用所有这些。
# Skip if not interested in multigpu.
class MultiGPULossCompute:
"A multi-gpu loss compute and train function."
def __init__(self, generator, criterion, devices, opt=None, chunk_size=5):
# Send out to different gpus.
self.generator = generator
self.criterion = nn.parallel.replicate(criterion,
devices=devices)
self.opt = opt
self.devices = devices
self.chunk_size = chunk_size
def __call__(self, out, targets, normalize):
total = 0.0
generator = nn.parallel.replicate(self.generator,
devices=self.devices)
out_scatter = nn.parallel.scatter(out,
target_gpus=self.devices)
out_grad = [[] for _ in out_scatter]
targets = nn.parallel.scatter(targets,
target_gpus=self.devices)
# Divide generating into chunks.
chunk_size = self.chunk_size
for i in range(0, out_scatter[0].size(1), chunk_size):
# Predict distributions
out_column = [[Variable(o[:, i:i+chunk_size].data,
requires_grad=self.opt is not None)]
for o in out_scatter]
gen = nn.parallel.parallel_apply(generator, out_column)
# Compute loss.
y = [(g.contiguous().view(-1, g.size(-1)),
t[:, i:i+chunk_size].contiguous().view(-1))
for g, t in zip(gen, targets)]
loss = nn.parallel.parallel_apply(self.criterion, y)
# Sum and normalize loss
l = nn.parallel.gather(loss,
target_device=self.devices[0])
l = l.sum()[0] / normalize
total += l.data[0]
# Backprop loss to output of transformer
if self.opt is not None:
l.backward()
for j, l in enumerate(loss):
out_grad[j].append(out_column[j][0].grad.data.clone())
# Backprop all loss through transformer.
if self.opt is not None:
out_grad = [Variable(torch.cat(og, dim=1)) for og in out_grad]
o1 = out
o2 = nn.parallel.gather(out_grad,
target_device=self.devices[0])
o1.backward(gradient=o2)
self.opt.step()
self.opt.optimizer.zero_grad()
return total * normalize
现在我们创建我们的模型、标准、优化器、数据迭代器和并行化
# GPUs to use
devices = [0, 1, 2, 3]
if True:
pad_idx = TGT.vocab.stoi["" ]
model = make_model(len(SRC.vocab), len(TGT.vocab), N=6)
model.cuda()
criterion = LabelSmoothing(size=len(TGT.vocab), padding_idx=pad_idx, smoothing=0.1)
criterion.cuda()
BATCH_SIZE = 12000
train_iter = MyIterator(train, batch_size=BATCH_SIZE, device=0,
repeat=False, sort_key=lambda x: (len(x.src), len(x.trg)),
batch_size_fn=batch_size_fn, train=True)
valid_iter = MyIterator(val, batch_size=BATCH_SIZE, device=0,
repeat=False, sort_key=lambda x: (len(x.src), len(x.trg)),
batch_size_fn=batch_size_fn, train=False)
model_par = nn.DataParallel(model, device_ids=devices)
None
开始训练
#!wget https://s3.amazonaws.com/opennmt-models/iwslt.pt
if False:
model_opt = NoamOpt(model.src_embed[0].d_model, 1, 2000,
torch.optim.Adam(model.parameters(), lr=0, betas=(0.9, 0.98), eps=1e-9))
for epoch in range(10):
model_par.train()
run_epoch((rebatch(pad_idx, b) for b in train_iter),
model_par,
MultiGPULossCompute(model.generator, criterion,
devices=devices, opt=model_opt))
model_par.eval()
loss = run_epoch((rebatch(pad_idx, b) for b in valid_iter),
model_par,
MultiGPULossCompute(model.generator, criterion,
devices=devices, opt=None))
print(loss)
else:
model = torch.load("iwslt.pt")
一旦经过训练，我们就可以对模型进行解码以生成一组翻译。这里我们简单地翻译验证集中的第一句话。这个数据集非常小，所以贪婪搜索的翻译相当准确。
for i, batch in enumerate(valid_iter):
src = batch.src.transpose(0, 1)[:1]
src_mask = (src != SRC.vocab.stoi["" ]).unsqueeze(-2)
out = greedy_decode(model, src, src_mask,
max_len=60, start_symbol=TGT.vocab.stoi[""])
print("Translation:", end="\t")
for i in range(1, out.size(1)):
sym = TGT.vocab.itos[out[0, i]]
if sym == "": break
print(sym, end =" ")
print("\n翻译结束")
print("Target:", end="\t")
for i in range(1, batch.trg.size(0)):
sym = TGT.vocab.itos[batch.trg.data[i, 0]]
if sym == "": break
print(sym, end =" ")
print()
break
附加内容：BPE、Search、Averaging
所以这主要涵盖了Transformer模型本身。有四个方面我们没有明确涉及。我们还在OpenNMT-py 中实现了所有这些附加功能。
- BPE/Word-piece：我们可以使用一个库来首先将数据预处理为子字单元。请参阅 Rico Sennrich 的subword-nmt实现。这些模型会将训练数据转换为如下所示：
▁Die ▁Protokoll datei ▁kann ▁ heimlich ▁per ▁E - Mail ▁oder ▁FTP ▁an ▁einen ▁bestimmte n ▁Empfänger ▁gesendet ▁werden .
- 共享嵌入：当使用带有共享词汇的 BPE 时，我们可以在源/目标/生成器之间共享相同的权重向量。有关详细信息，请参阅 引用。要将其添加到模型中，只需执行以下操作：
if False:
model.src_embed[0].lut.weight = model.tgt_embeddings[0].lut.weight
model.generator.lut.weight = model.tgt_embed[0].lut.weight
- Beam 搜索: 这有点过于复杂，无法在此介绍。有关 pytorch 实现，请参阅OpenNMT-py
- 模型平均：论文对最后k个检查点进行平均以创建集成效果。如果我们有一堆模型，我们可以事后这样做：
def average(model, models):
"Average models into model"
for ps in zip(*[m.params() for m in [model] + models]):
p[0].copy_(torch.sum(*ps[1:]) / len(ps[1:]))
结论
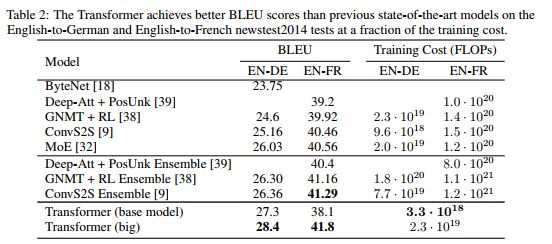
在 WMT 2014 英德翻译任务中，大transformer 模型（表 2 中的 Transformer (big)）比先前报告的最佳模型（包括集成）高出 2.0 BLEU 以上，建立了新的BLEU 得分为 28.4。该模型的配置列在表 3 的底部。在 8 个 P100 GPU 上训练需要 3.5 天。甚至我们的基础模型也超过了所有先前发布的模型和集成模型，其训练成本仅为任何竞争模型的一小部分。
在 WMT 2014 英法翻译任务中，我们的大模型获得了 41.0 的 BLEU 分数，优于之前发布的所有单个模型，训练成本不到之前最先进技术的 1/4模型。为英语到法语训练的 Transformer（大）模型使用dropout率 Pdrop = 0.1，而不是 0.3。
我们在这里编写的代码是基本模型的一个版本。此处提供了该系统的完全训练版本示例模型。
通过上一节中的附加扩展，OpenNMT-py 复制在 EN-DE WMT 上达到 26.9。在这里，我已将这些参数加载到我们的重新实现中。
!wget https://s3.amazonaws.com/opennmt-models/en-de-model.pt
model, SRC, TGT = torch.load("en-de-model.pt")
model.eval()
sent = "▁The ▁log ▁file ▁can ▁be ▁sent ▁secret ly ▁with ▁email ▁or ▁FTP ▁to ▁a ▁specified ▁receiver".split()
src = torch.LongTensor([[SRC.stoi[w] for w in sent]])
src = Variable(src)
src_mask = (src != SRC.stoi["" ]).unsqueeze(-2)
out = greedy_decode(model, src, src_mask,
max_len=60, start_symbol=TGT.stoi[""])
print("Translation:", end="\t")
trans = " "
for i in range(1, out.size(1)):
sym = TGT.itos[out[0, i]]
if sym == "": break
trans += sym + " "
print(trans)
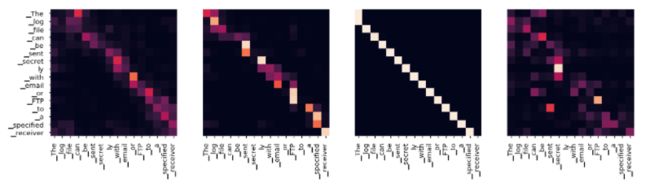
注意力可视化
即使使用贪婪的解码器，翻译看起来也不错。我们可以进一步将其可视化，以查看注意力的每一层发生了什么
tgt_sent = trans.split()
def draw(data, x, y, ax):
seaborn.heatmap(data,
xticklabels=x, square=True, yticklabels=y, vmin=0.0, vmax=1.0,
cbar=False, ax=ax)
for layer in range(1, 6, 2):
fig, axs = plt.subplots(1,4, figsize=(20, 10))
print("Encoder Layer", layer+1)
for h in range(4):
draw(model.encoder.layers[layer].self_attn.attn[0, h].data,
sent, sent if h ==0 else [], ax=axs[h])
plt.show()
for layer in range(1, 6, 2):
fig, axs = plt.subplots(1,4, figsize=(20, 10))
print("Decoder Self Layer", layer+1)
for h in range(4):
draw(model.decoder.layers[layer].self_attn.attn[0, h].data[:len(tgt_sent), :len(tgt_sent)],
tgt_sent, tgt_sent if h ==0 else [], ax=axs[h])
plt.show()
print("Decoder Src Layer", layer+1)
fig, axs = plt.subplots(1,4, figsize=(20, 10))
for h in range(4):
draw(model.decoder.layers[layer].self_attn.attn[0, h].data[:len(tgt_sent), :len(sent)],
sent, tgt_sent if h ==0 else [], ax=axs[h])
plt.show()
Encoder Layer 2
其他层省略…
欢迎关注公众号：
