从傅里叶变换，到短时傅里叶变换，再到小波分析（CWT），看这一篇就够了（附MATLAB傻瓜式实现代码）

本专栏中讲了很多时频域分析的知识，不过似乎还没有讲过时频域分析是怎样引出的。

所以本篇将回归本源，讲一讲从傅里叶变换→短时傅里叶变换→小波分析的过程。

为了让大家更直观得理解算法原理和推导过程，这篇文章将主要使用图片案例。

一、频谱分析？——还不够

频谱分析可以告诉我们一个信号包含哪些频率的信息以及这些频率的强度。

通过频谱分析我们可以将信号从其原始的时间域（即随时间变化的形式）转换到频域（即按频率分布的形式）。

如果对此你不懂的话，那么我推荐你读一下这篇文章：Heinrich：如果看了这篇文章你还不懂傅里叶变换，那就过来掐死我吧。

频谱分析是如此常用的工具，如果你在做信号处理的研究领域，几乎不可能没听过它。

然而，传统的傅里叶变换有一个限制：它假设信号是平稳的，即其频率成分不会随时间改变。

对于那些随时间变化其频率特性的信号（比如音乐或语音），这种假设并不成立，因此传统的频谱分析无法准确地描绘这些信号的频率随时间的变化情况。

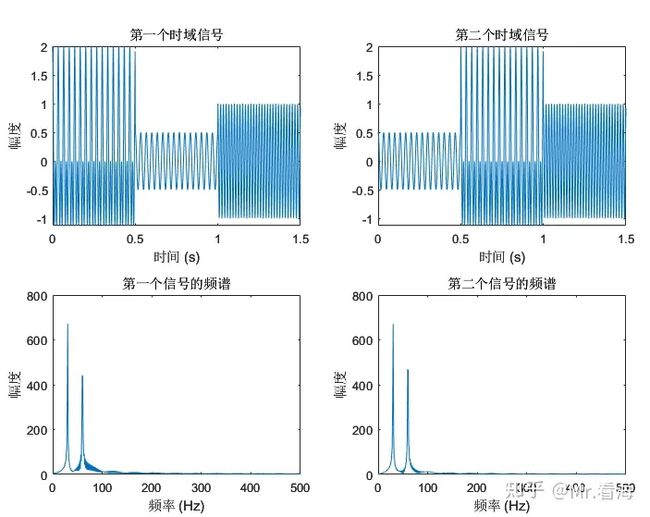
举个可能不太恰当的例子，当你唱“宫廷玉液酒”和“玉液宫廷酒”时，声音信号可能在频谱上差别不大。

我们可以用一张图演示这个现象：

“宫廷玉液酒”和“玉液宫廷酒”——两个不同的信号，他们的频谱是类似的

可见当信号的频率成分随时间显著变化时，即所谓的非平稳信号，传统频谱分析就不太合适了。举几个例子：

• 研究信号的局部特性：如爆炸声、机器的故障噪声等，这些信号的特性在短时间内变化很大。
• 语音处理：在自动语音识别和语音合成中，语音的特征如音高和音量随着时间而变化。
• 雷达和无线电信号分析：雷达信号的特性依赖于时间和观测的角度，需分析这些信号随时间的变化。
• 生物医学信号分析：比如心电图（ECG）和脑电图（EEG）这样的生理信号，它们的频率特性随时间改变。

二、直观的解决思路——给频谱分析加窗

传统的频谱分析是全面的，它给出了整个信号的平均频率内容，却无法告诉我们这些频率成分是怎样随时间变化的。

这就好比是我们闭上眼睛听整首曲子，然后试图回忆每个乐器何时加入。这个任务对于我们的大脑来说是非常困难的，对于数学工具来说也同样困难。

这里就需要一种方法来解决这个问题，而“加窗”提供了一个直观的解决思路。

加窗，简单来说，就是在分析信号时不是一次性看整个信号，而是只看信号的一个小段，这个小段就是一个“窗口”。

通过在信号上滑动这个窗口，我们可以逐渐查看整个信号，就像是通过一系列快照来观察它的变化。

这个过程可以用一个日常的比喻来说明：想象你正在看一场烟花表演，你决定用相机拍摄整个表演。如果使用长时间曝光，你最终得到的照片将是所有烟花的叠加，这相当于传统的频谱分析；然而，如果你使用一连串短时间曝光的快照，每张照片将捕捉到表演的一个瞬间，这就类似于“加窗”的频谱分析。

在实际应用中，我们选择一段时间内的信号，对它进行傅里叶变换，这样得到的频谱只代表了那段时间内的信号。然后，我们移动窗口到下一个时间段，再做一次变换，如此反复。最后，我们将所有的频谱组合起来，就能够得到一个动态的频谱图，这个图不仅展示了信号的频率成分，还展示了它们是如何随时间变化的——这个过程就是短时傅里叶变换（Short-Time Fourier Transform， STFT）。

其计算过程可以用一张动图生动地展示出来：

短时傅里叶变换STFT计算过程

STFT图就是频谱图在时间轴上的连续展开，这个图有三个轴：

• 时间轴：表示信号分析的持续时间。
• 频率轴：它表示了信号中存在的各种频率成分。
• 幅度轴：幅度轴垂直于时间-频率平面，通常通过颜色的深浅来表示。强度表示在特定时间和频率下信号的能量大小。

STFT图也有二维形式，这种形式中是使用颜色来代表幅度大小的，其生成过程如下：

二维STFT图绘制过程

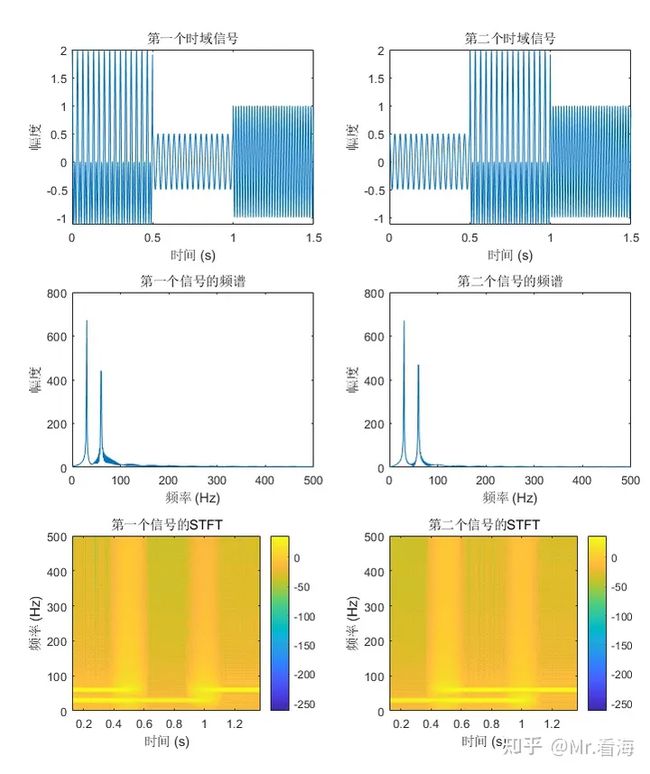
返回到上边“宫廷玉液酒”和“玉液宫廷酒”的例子，我们画一下其STFT图：

在STFT中可以看到两个信号的区别了

对比第一个信号和第二个信的STFT图，可以看到在不同时间段内频率成分的变化。

通过比较这些图，可以直观地看出STFT与传统傅里叶变换的区别。STFT揭示了信号的局部时频特性。这就是为什么STFT特别适用于显示信号中频率成分随时间的变化。

三、成也窗口，败也窗口——从短时傅里叶变换到小波分析

在短时傅里叶变换（STFT）中，窗口函数及其大小选择是分析的关键。窗口函数决定了在任何给定时间点，信号的哪一部分被用于分析。窗口大小的选择直接影响了分析结果的时间分辨率和频率分辨率，这是进行有效STFT分析的最重要的权衡。

窗口大小的时间分辨率影响：时间分辨率与窗口的宽度密切相关。一个窄窗口提供较高的时间分辨率，因为它捕捉了信号在很短时间内的变化。这对于分析包含快速变化的瞬态事件，如敲击声或爆炸声，是非常有用的。然而，较小的窗口将限制频率分辨率，因为频率分析需要足够的周期来准确估计。

窗口大小的频率分辨率影响：频率分辨率与窗口的宽度呈反比。一个宽窗口覆盖了信号的较长时间段，提供了较高的频率分辨率。这是因为更多的周期可以在窗口内被分析，从而更准确地确定低频成分。但是，这会牺牲时间分辨率，因为窗口中的信号被假定在这段时间内是平稳的。

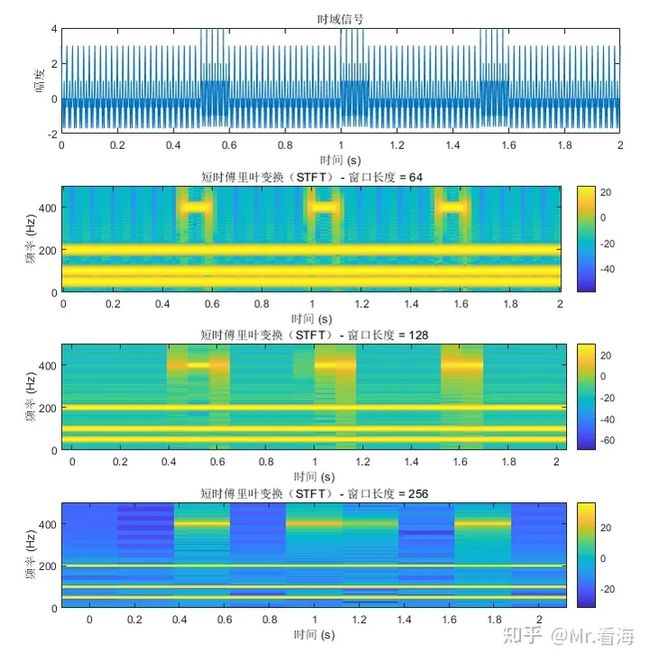
只靠文字可能不够直观，还是来看图吧：

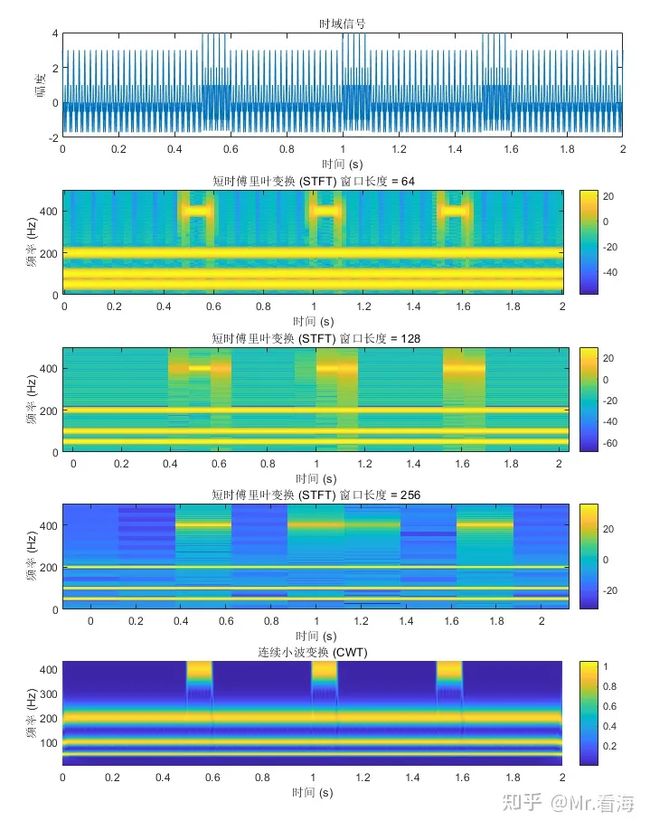
• 小窗口长度（例如64样本）： 小窗口提供较高的时间分辨率，这意味着可以更精确地看到频率变化的时间位置（即0.5s-0.6s）。例如，短暂的频率跳变将在图中更清晰地显示为突然的颜色变化。然而，频率分辨率较低，这意味着看不清楚具体是哪个频率发生了变化，频率成分可能会显得模糊。
• 中等窗口长度（例如128样本）： 中等大小的窗口提供了时间分辨率和频率分辨率之间的折衷。会看到频率跳变不如小窗口那样清晰，但频率的分辨率会更好一些，使得不同的频率成分更加明显。
• 大窗口长度（例如256样本）： 大窗口提供较高的频率分辨率，您将能够看到信号中不同频率成分的细节，就像200Hz的频率可以被很好得识别出来。然而，时间分辨率较低，这意味着短暂事件的精确时间定位可能不太清晰，图中跳变的时间段都延展到0.4-0.6s了，而实际上它是0.5-0.6s。

总结一句话，上述矛盾体现了所谓的测不准原理，即时空域和频域无法同时准确。

在实际的信号处理工作中，选择窗口大小常常是基于对信号特性的了解以及对分析精度需求的权衡。如果事件的时间特性是分析的关键，那么小窗口可能更合适；如果频率分辨率是关键，那么大窗口可能更优。

那有没有一种可能，窗口大小是可调的呢？

是的——小波分析就可以实现！

四、小波分析到底是怎么计算的

4.1 又双叒叕说卷积

“卷积”的概念在本专栏里是明星选手了，还不熟悉卷积的同学可以看这里：Mr.看海：这篇文章能让你明白卷积。

我们回忆一下卷积的重要特性：频域相乘等于时域的卷积。

那么频域分析我们可以从一种独特的视角来看：想象一下，我们从频率为0的正弦波开始，逐渐增加这个频率，同时记录每个频率的正弦波与原始信号卷积的结果。这样，我们可以绘制出一张图，其横轴表示频率，纵轴表示卷积结果的强度。请问得到的结果是什么？

是的，就（近似）是频谱！

为什么？因为1Hz的频谱为一个在1Hz处的脉冲，这个脉冲乘以原始信号的频谱得到的就是原始信号1Hz处的频谱幅值，转换到时域上就是原始信号与这个1Hz的正弦信号的卷积。

动图又来了，看过后相信你就能明白：

频谱计算的一种理解视角——频谱可以被视为一系列不同频率的正弦波与原始信号进行卷积的结果。

然而，这种方法只能提供频率上的信息，毕竟中间图中的正弦无论如何平移，都不会影响到频谱的结果。

聪明的你应该想到解决方案了。

4.2 当小波遇上卷积

是的，我们可以将无限延展周期性的正弦波换成时变的信号，比如这样的：

Meyer小波的图像

这样一个信号，就同时可以做拉伸（频率上变换）和平移（延迟时间上变换）了。

依然采用上述卷积计算的方式，来求小波变换的结果，此时画出来的图就不是频谱这样的二维图，而是一个三维图了，就像下边这样：

小波变换过程（示意图，计算可能不太严谨）

我们重点看中间的小波的图像，它在时间轴上进行平移，每平移一次进行一次卷积运算，计算结果在第三张图上按照对应的时间（由位置决定）和频率（由尺度决定）画出计算结果。仔细观察小波的变换，可以发现其特点：高频部分具有较高的时间分辨率和较低的频率分辨率，而低频部分具有较高的频率分辨率和较低的时间分辨率，这就恰好解决了STFT的痛点。（PS：小波是复信号，上图中只画了实部投影）

再回到反映STFT中时空域和频域测不准原理这张图，如果我们用小波分析处理同样的信号，得到的结果是这样的：

增加了最后一张图——CWT变换结果

在最下边这张图中可以清晰地显示信号中的所有频率分量及其随时间的变化。三个突变信号的边缘清晰锐利、三个主要频率的分辨也较为清晰可辨，在时间分辨率和频率分辨率的取舍中找到了完美的平衡点。

最后以一个优美（误）的比喻来结束理论讲解部分吧：

频谱分析是长曝光的艺术，揭示了振动的连续舞蹈；短时傅里叶变换像是定焦的高速连拍，捕捉时间的每一跳动。而小波分析赋予了相机变焦的魔力，让每帧都能自适应地聚焦于故事的精髓，无论是宏伟的篇章还是微妙的细节。

五、短时傅里叶变换（STFT）和小波分析（CWT）的MATLAB代码实现

笔者对STFT和CWT算法画图程序分别进行了封装，同学们在调用的时候可以方便轻松很多。

5.1 STFT画图（二维图+三维图）

短时傅里叶变换画图常用设置参数就四个：窗口类型、窗口大小、窗口重叠大小、每个窗口上执行FFT的点数。选择合适的参数对于获取准确和有用的频谱分析至关重要。以下是这四个参数的详细说明及其对STFT结果的影响：

1. 窗口类型：窗口类型决定了信号在时频分析中的平滑程度。常用的窗口类型包括汉明窗、汉宁窗和矩形窗。不同的窗口类型会影响频谱的泄露和分辨率。例如，矩形窗提供最高的频率分辨率，但其频谱泄漏也最大；而汉明窗和汉宁窗则提供更好的频谱平滑性，适用于波形变化不是非常快的信号。
2. 窗口大小：窗口大小决定了频率分辨率和时间分辨率之间的权衡。较大的窗口提供更高的频率分辨率但较低的时间分辨率，而较小的窗口则相反。
3. 窗口重叠大小：窗口重叠用于提高时间分辨率并减少数据丢失。较大的重叠程度可以提供更平滑的频谱表示，但计算成本也更高。
4. 每个窗口上执行FFT的点数：这决定了频谱的频率分辨率。通常，FFT点数至少应等于窗口大小，它通常取2的整数次幂，比如128、256这种。

好了，知道要设置的参数，代码实现就很简单了，就像这样：

% 设置STFT参数
windowType = @hamming;  % 设置窗口类型为 Hamming 窗口
windowSize = 100;       % 设置窗口大小为 100 样本
overlap = 98;           % 设置窗口重叠为 98 样本
FFTLength = 128;        % 设置在每个窗口上执行FFT的点数为 128

% 调用 pSTFT2D 函数
% 使用上述设置对数据进行短时傅里叶变换，并绘制二维图形
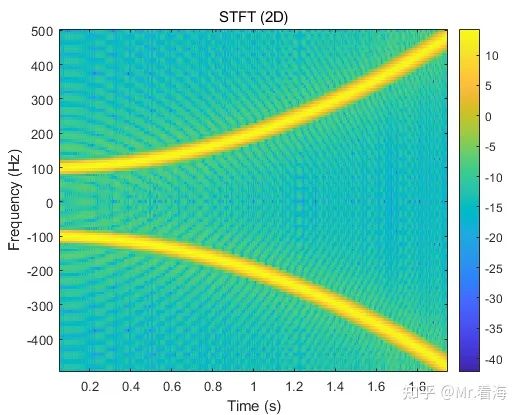
pSTFT2D(data, Fs, windowType, windowSize, overlap, FFTLength);

此时就可以画出这样的结果：

STFT的二维结果图

如果想画三维结果也可以，只需要写：

% 调用 pSTFT3D 函数
% 使用相同的设置对数据进行短时傅里叶变换，并绘制三维图形
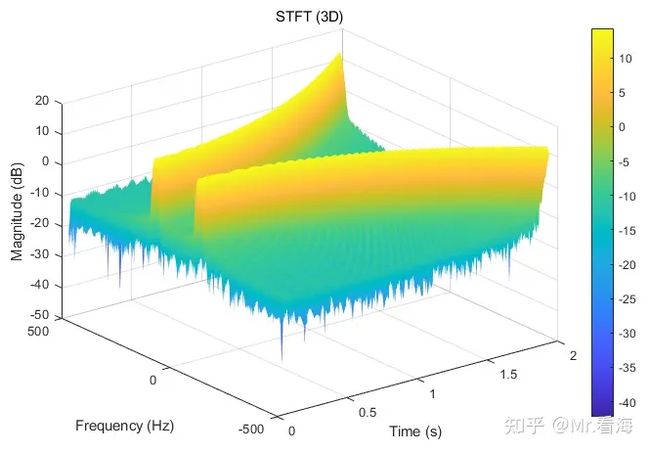
pSTFT3D(data, Fs, windowType, windowSize, overlap, FFTLength);

此时可以画出：

STFT的三维结果图

是不是既简单又酷炫。上边代码中的pSTFT2D和pSTFT3D是笔者封装的函数，文末可以获取哈。

5.2 CWT画图（二维图+三维图）

连续小波变换的图需要设置的参数就比较少了，这就很适合选择困难症的同学们。

通常情况下，只需要选择小波类型就可以，甚至类型也不需要费心选，使用默认的Morse就可以。

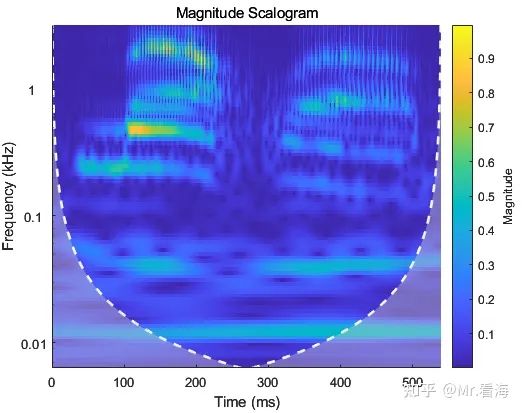
不过同学们也许会在论文中看到CWT的图是这样的：

连续小波变换图

在这个图上，有一个锥形或者半圆形的边界。这种边界通常表示“锥形区域”（Cone of Influence, COI），用于指出小波变换结果中的边缘效应。

在小波分析中，信号的开始和结束部分可能会因为缺乏足够的数据而产生不可靠的变换结果。由于小波变换涉及到信号的缩放和平移，信号的边缘部分在变换过程中可能会“跑出”数据的实际范围，导致这些区域的变换结果被信号之外的零填充或其他形式的边界处理影响。锥形区域边界内的变换结果被认为是可靠的，而边界外的变换结果可能会受到边缘效应的影响，因此在解释这部分结果时需要格外小心。

画这样一张图需要四行代码：

% 情况1：绘制锥形区域
plotCone = true;     % 设置绘制锥形区域为 true
freqScale = 'log'; % 当绘制锥形区域时，freqScale 参数不影响输出，都会为对数坐标
waveletName = 'morse'; % 设置小波名称为 Morse
% 调用 pCWT 函数，传入上述参数并获取结果
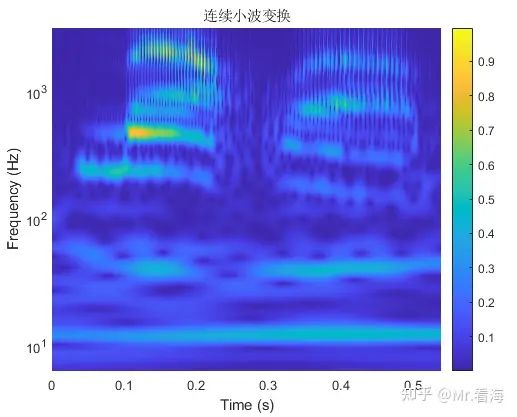
[timeAxis, freqAxis, cwtData] = pCWT(data, waveletName, Fs, plotCone, freqScale);

有些同学表示，不想要锥形区域，就要单纯的CWT结果，这个我也给出了选择余地——把plotCone设置为false即可：

% 情况2：不绘制锥形区域，使用对数频率轴
plotCone = false;     % 设置绘制锥形区域为 false
freqScale = 'log';   % 设置频率轴类型为对数
waveletName = 'morse'; % 设置小波名称为 Morse
% 调用 pCWT 函数，传入上述参数并获取结果
[timeAxis, freqAxis, cwtData] = pCWT(data, waveletName, Fs, plotCone, freqScale);

去掉了锥形区域

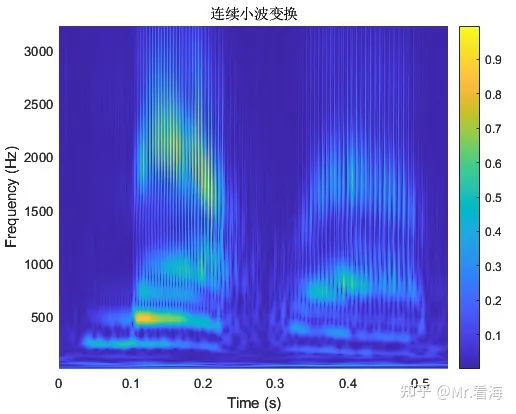
有细心的同学发现了，上边两张图的频率轴是取对数的结果，但是我就是想要线性的——也可以！把freqScale设置为'linear'：

% 情况3：不绘制锥形区域，使用线性频率轴
plotCone = false;    % 设置不绘制锥形区域
freqScale = 'linear';% 设置频率轴类型为线性
waveletName = 'morse'; % 设置小波名称为 Morse
% 调用 pCWT 函数，传入上述参数并获取结果
[timeAxis, freqAxis, cwtData] = pCWT(data, waveletName, Fs, plotCone, freqScale);

线性频率轴

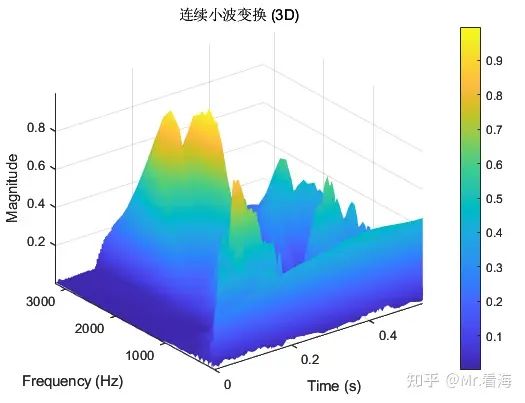
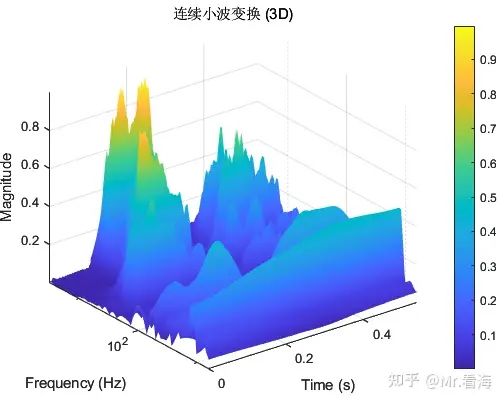
有同学又表示，我要像STFT一样要三维图！好吧，我也准备了（而且可以选择频率轴线性坐标或者对数坐标）：

% 情况1：使用线性频率轴绘制三维图
freqScale = 'linear';
waveletName = 'morse'; % Morse 小波
[timeAxis, freqAxis, cwtData] = pCWT3D(data, waveletName, Fs, freqScale);


% 情况2：使用对数频率轴绘制三维图
freqScale = 'log';
waveletName = 'morse'; % Morse 小波
[timeAxis, freqAxis, cwtData] = pCWT3D(data, waveletName, Fs, freqScale);

频率轴为线性坐标的三维CWT图

频率轴为对数坐标的三维CWT图

至此，大家的需求应该都可以满足了吧！

获取代码

上边的测试代码和封装函数，包括工具箱都可以在下边的链接获取：

连续小波变换CWT画图代码 - 工具箱文档 | 工具箱文档

短时傅里叶变换STFT画图代码 - 工具箱文档 | 工具箱文档

编程不易，感谢支持~