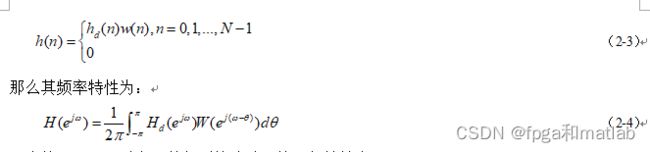基于窗函数的FIR滤波器的matlab设计与实现

目录

一、理论基础

1.1 FIR滤波器概述

1.2 FIR滤波器理论介绍

二、核心程序

三、仿真测试结果

---

一、理论基础

1.1 FIR滤波器概述

      数字滤波器的设计是现代数字信号处理的重要内容。常用的数字滤波器有FIR和IIR两种类型，两者比较而言。主要有如下几点区别：

      从系统的幅频特性来看，IIR滤波器由于综合利用了系统的零极点，容易达到比较理想的设计效果； 而FIR滤波器由于只有零点，效果较IIR滤波器差。要达到与IIR滤波器相似的效果，往往要提高系统的阶数。

      其次，从相位特性来看，用FIR滤波器可以得到线性相位数字滤波器，满足信号不失真传输的要求。 对于IIR滤波器而言，往往幅频特性越好，相位非线性就越严重。

       再次，从系统稳定性来看，FIR滤波器由于没有极点，所以一定是稳定的；而IIR滤波器的稳定与否取决于其极点的位置。

      最后，从设计方法来看，IIR滤波器的设计参照连续时间系统的传输函数进行，可以充分利用模拟滤波器的设计结果，但是要求设计者有一定的模拟滤波器的设计知识，而且必须保证在模拟滤波器中能够找到合适的滤波器原型作为设计基础；而FIR滤波器设计结果完全是根据系统频率进行，不需要设计者有其他滤波器的知识，设计方法比较简单。

       FIR(Finite Impulse Response)滤波器是一种常用的数字滤波器，其特性由一组称为“滤波器系数”或“滤波器抽头”的数值定义。基于窗函数的FIR滤波器设计是一种常用的设计方法，其主要原理是通过窗函数来截取理想滤波器的单位脉冲响应，以获得实际的FIR滤波器。窗函数法设计FIR滤波器的基本原理是：首先根据所要求的滤波器频率特性，设计出一个理想的滤波器频率响应，然后截取该频率响应的脉冲响应，得到实际的FIR滤波器的脉冲响应。窗函数法设计的关键是选择合适的窗函数和理想滤波器的频率响应。

公式：

1. 理想滤波器的频率响应：H(e^jw) = Hd(e^jw) * W(e^jw)
   其中，Hd(e^jw)为理想的频率响应，W(e^jw)为窗函数的频率响应。
2. 理想滤波器的脉冲响应：h(n) = hd(n) * w(n)
   其中，hd(n)为理想的脉冲响应，w(n)为窗函数的脉冲响应。
3. 窗函数：常用的窗函数有矩形窗、汉宁窗、汉明窗、高斯窗等。

实现步骤：

1. 确定滤波器的性能指标（如过渡带宽、阻带衰减等），设计理想的频率响应 Hd(e^jw)。
2. 选择合适的窗函数 W(e^jw)，使其频率响应与理想的频率响应匹配。
3. 计算实际滤波器的脉冲响应 h(n)，通过时域卷积 hd(n) * w(n)。
4. 根据 h(n) 实现 FIR 滤波器，通常可以使用直接型、级联型或频率采样型结构。
5. 对设计的滤波器进行性能评估，如不满足要求，可能需要重新选择窗函数或修改理想的频率响应。

这是一个基本的步骤和原理，具体实现可能会根据具体的应用和性能要求有所不同。

1.2 FIR滤波器理论介绍

 

通常情况下，通过窗函数得到的滤波器的理想特性为：

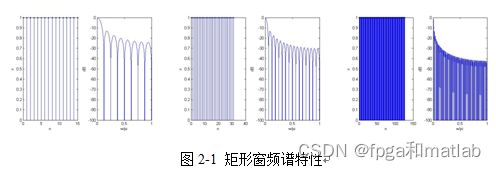
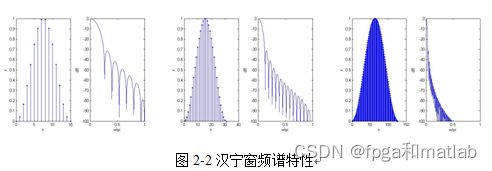
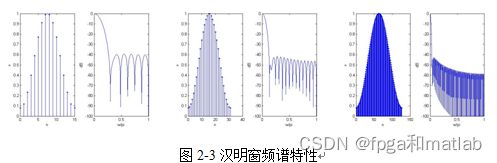
    ·截止频率的间断点变成了连续的曲线，使其出现了一个过渡带，它的宽度等于窗函数的主瓣的宽度。所以，窗函数的主瓣越宽，过渡带就越宽。

    ·由于窗函数旁瓣的影响，使得滤波器的幅度频率特性出现了波动，波动的幅度取决于旁瓣的相对幅度.旁瓣范围的面积越大，通带波动和阻带的波动就越大，即阻带的衰减减小。而波动的大小，取决于旁瓣的大小。

     ·增加窗函数的长度，只能减少窗函数的幅度频率特性的主瓣宽度，而不能减少主瓣和旁瓣的相对值，该值取决于窗函数的形状。换句话说，增加截取函数的长度N只能相应的减小过渡带，而不能改变滤波器的波动程度。

    常用的窗函数有矩形窗、海明窗、凯塞窗、汉宁(HanZning)窗等。

二、核心程序

clc,clear


Ts=1/1000  ;%设置采样频率
N=128;      %设置阶数
n=[0:(N-1)];
Wn=0.2;     %设置截止频率

t=0:Ts:3*pi;
y=sin(2*pi*t)+cos(8*pi*t)+cos(400*pi*t);

figure(1);plotspec(y,Ts);title('y');


%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法
%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法%窗函数采样法
k=input('请选择窗的类型:\n 1、矩形窗\n 2、汉宁窗\n 3、汉明窗\n 4、布拉克曼窗\n');
switch k
    case 1
        x=win(0,N-1,0,N-1);                       %矩形窗
        figure,
        subplot(1,2,1);
        stem(n,x,'.');                            %得到数字信号波形表示方法函数STEM
        xlabel('n');                              %X坐标标签
        ylabel('x');                              %Y坐标标签
        string=['矩形窗时域图形','N=',num2str(N)];%波形标题
        text((0.6*N),0.8,string);                 %波形标题
        
        [H,m]=freqz(x,[1],1024,'whole');          %求其频率响应
.......................
        
    case 2
        x=win(0,N-1,0,N-1);
        x=(0.5-0.5*cos(2*pi*n/(N-1))).*x;
        figure,
        subplot(1,2,1);
        stem(n,x,'.');
        xlabel('n');
        ylabel('x');
        string=['汉宁窗时域图形','N=',num2str(N)];
        text((0.6*N),0.8,string);
        
........................
    case 3
        x=win(0,N-1,0,N-1);
        x=(0.54-0.46*cos(2*pi*n/(N-1))).*x;
        figure,
        subplot(1,2,1);
        stem(n,x,'.');
        xlabel('n');
        ylabel('x');
        string=['汉明窗时域图形','N=',num2str(N)];
        text((0.6*N),0.8,string);
        
............................       

    case 4
        x=win(0,N-1,0,N-1);
        x=(0.42-0.5*cos(2*pi*n/(N-1))+0.08*cos(4*pi*n/(N-1))).*x;
        figure,
        subplot(1,2,1);
        stem(n,x,'.');
        xlabel('n');
        ylabel('x');
        string=['布拉克曼窗时域图形','N=',num2str(N)];
        text((0.6*N),0.8,string);
        
.................................            

    
end

 

三、仿真测试结果

A25-002