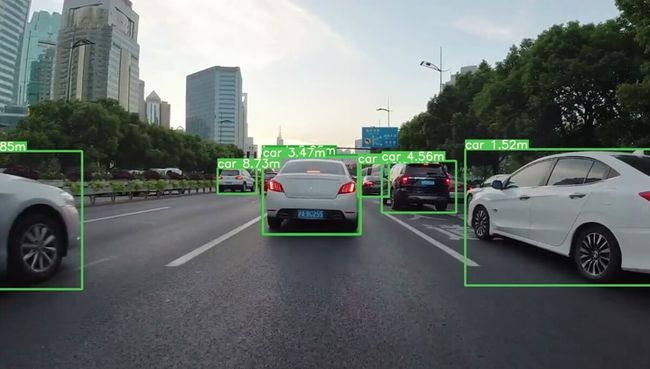
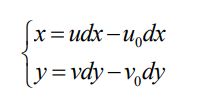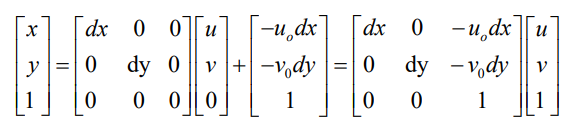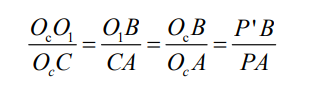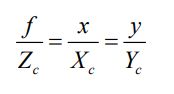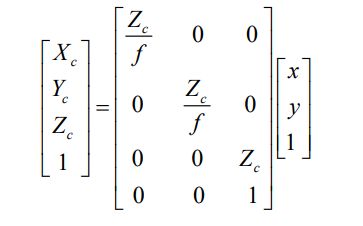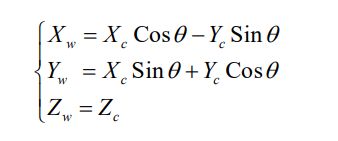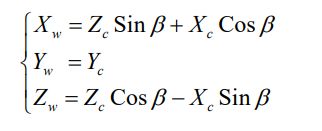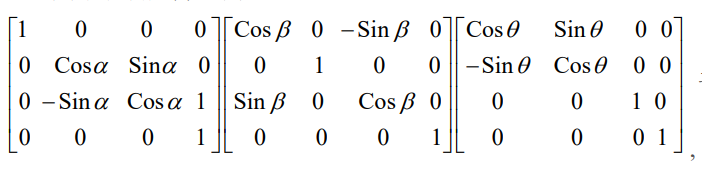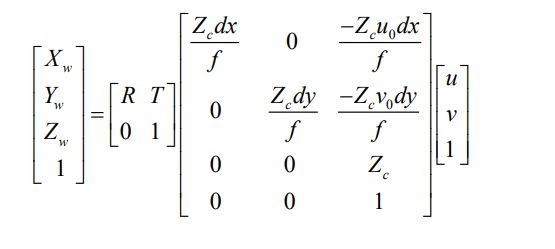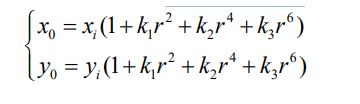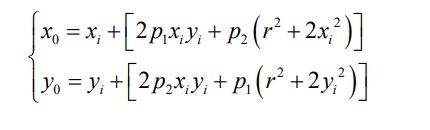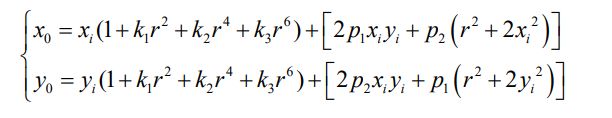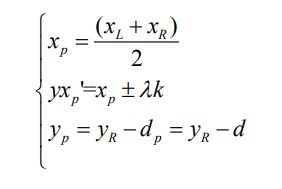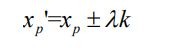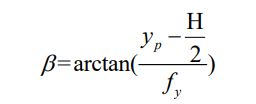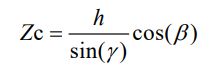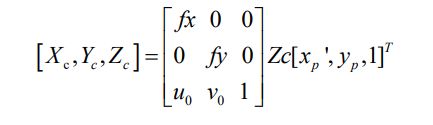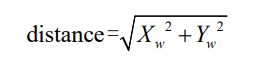单目测距+代码部署（目标检测+车辆/行人等测距）

本文主要讲述了如何运用单目摄像头进行距离测量，在完成yolo目标检测后我们可以对检测到的目标框进行距离测量。

单目视觉测距与双目视觉测距对比

测距在智能驾驶的应用中发挥着重要作用。测距方法主要包含两类：主动测 距与被动测距，主动测距是当前研究的热点内容之一。主动测距方法包括采用传 感器、摄像机、激光雷达等车载设备进行测距。摄像头由于价格相对低廉且性能 稳定应用较为广泛，本文采用摄像头进行距离测量。

单目测距与双目测距优缺点对比

1.单目测距主要运用测距模型结合目标矩形框来进行测距任务，通过目标在图 像中的大小位置信息去估算距离。单目测距算法具有计算量小、成本低廉的优点， 并且测距误差也可以通过后续的调校来消除，很多算法都在采用基于单目视觉传 感器来开发产品。因此相对其他测距方法，单目视觉有更成熟的算法，本文亦采 用单目视觉测距。 利用双目视觉可以获取同一物体在成像平面上的像素偏移量。然后可以使用 相机焦距、像素偏移以及两个相机之间的实际距离从数学上得出对象之间的距离。 与单目测距相比，双目测距虽然更加精确，不需要数据集，但计算量大，速度相 对较慢，而且由于使用了两个摄像头，成本也变得更高。

2.相机成像模型

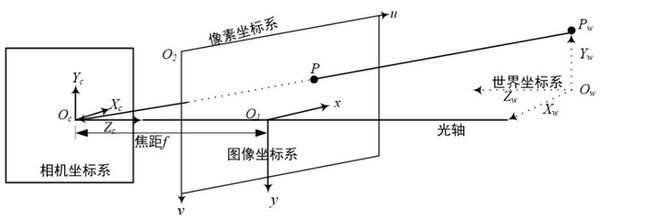
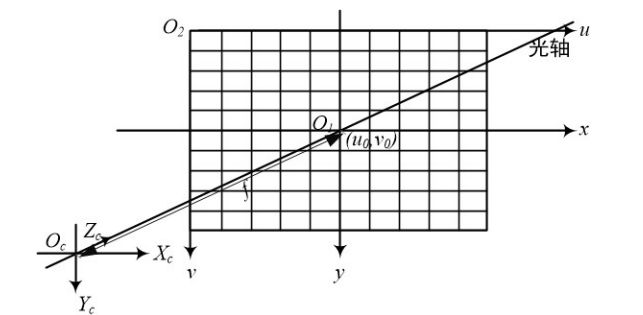
想要得到距离信息需要获得三维真实世界里的点，而由于处理的对像是摄像 头捕捉后的二维平面图像，因此如何将二维图像上的某个点转换为三维世界里的 点是值得考虑的问题。进一步的，把图像上的点转换到真实世界的点，就需要进 56 行像素坐标系、图像坐标系、相机坐标系以及世界坐标系之间的相互转换。四种 坐标系之间的相互关系如图 5-1 所示。坐标系描述如下：

(1)像素坐标系。数字图像一般是三维图像并且由众多像素点组合而成的，像 素坐标系的原点为 O2，以宽度方向为 u 轴，以高度方向为 v 轴。

(2)图像坐标系。图像坐标原点为 O1，并且像素坐标系和图像坐标系是平行的， 以图像宽度方向为 x 轴，以高度方向为 y 轴，长度单位为 mm。

(3)相机坐标系。相机坐标系原点 Oc，Xc轴、Yc 轴分别是与图像坐标系下的 x 轴、y 轴相互平行，相机 Zc轴和摄像头光轴重合。

(4)世界坐标系。我们所处的环境即是在世界坐标系之下，也就是图 5-1 中 Xw-Yw-Zw 平面。Pw 通过真实世界上的一点至图像上的 P 点，完成从世界坐标到 图像上坐标的转换。

坐标系转换

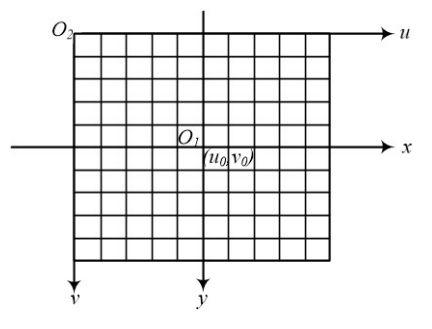
（1)像素坐标系转换到图像坐标系 像素坐标系是以像素来表示各个像素位置信息的，但是它不能够表达出图像 中物体的物理大小，因此需要进行坐标系之间的转换。

图像坐标系的坐标(x，y)与像素坐标系的坐标(u，v)之间的关系 可以表示为：

(u0,v0)是图像中心的像素坐标，dx、dy 分别是横向和纵向像素在感光板 上的单位物理长度。

写成齐次坐标矩阵的形式为：

(2)图像坐标系变换到相机坐标系

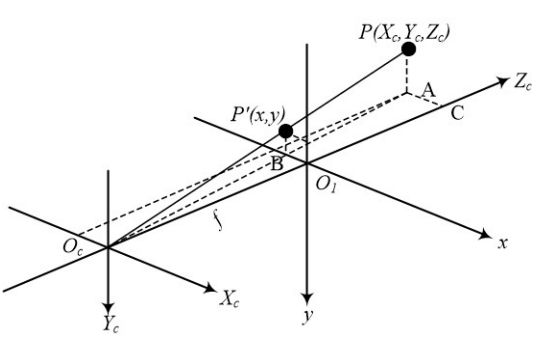
，OcO1之间的距离为焦距 f。图 5-4 表示了物体成像到图像坐标系 的过程，P 点、 P＇点分别为相机坐标系和图像坐标系下的坐标。

由上图易知，三角形 OcO1B 和三角形 OcCA 相似，三角形 OcBP＇和三角形 OcAP 相似，根据相似三角形原理有：

并且 OcO1的距离为焦距 f，结合 P(Xc,Yc,Zc)，P＇(x,y)点坐标，上式可写为：

进一步推倒可得：

将其写成齐次坐标矩阵的形式为：

(3)相机坐标系变换到世界坐标系

相机坐标系变换到世界坐标系可以描述为一个旋转平移的过程，分别将旋转 和平移的分量加起来就是整个坐标系转换的全过程了。对于旋转过程，假设相机 坐标系的 Z

同理，绕 X 轴旋转会得到如下关系

绕 Y 轴旋转会得到如下关系：

对于平移分量来说，可以表达为：

得到平移向量和旋转矩阵后，从相机坐标系变换到世界坐标系的公式可以完 整的写为：

其中旋转矩阵 R 为：

平移矩阵 T 表 示为：Tx Ty Tz 。结合式就完成了从像素坐标系到世界 坐标系的转换，整合起来为：

这样针对图像上的一个点，就可以利用上述公式结合相机内外参数求解出具 体的距离值。

三，相机内外参数与畸变系数

相机内外参数对图像矫正和测距具有重要意义。内外参数以及畸变系数可以 通过相机标定得到机。并且相机都会发生畸变，这对于测量来说显然是不能容忍 的，因此消除畸变是十分有必要的。

四，相机内外参数

等号右端第一项为相机的外参数，等号右端第二项表示为相 机内参数，内参属于相机内在属性。式中未知参数 Zc表示物体到光学中心的距离。 同时也说明了，在相机标定的过程中，如果物体相对于相机的位置不同，那么需 要对于每一个位置都需要去进行相机标定。

五，相机畸变系数

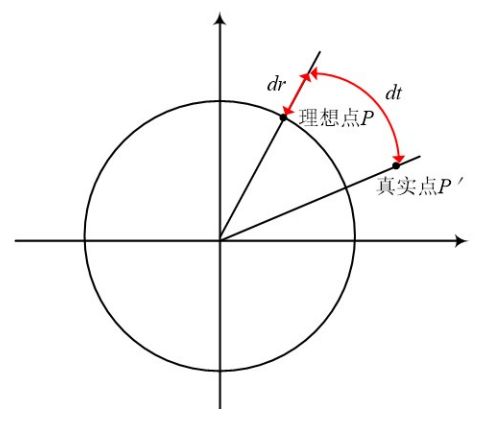
相机畸变造成了图像平面上某一像素点的真实位置与理想位置不完全重合的 现象，因此了解相机畸变现象并对相机进行矫正十分有必要。相机畸变主要包括 径向畸变和切向畸变二类。图 5-6 展示了畸变模型，对于平面上任意理论点 P，由 与畸变的存在，会使得 P 点偏移到 P＇点。图中 dr 表示相机的径向畸变，dt 表示 相机的切向畸变。

(1) 径向畸变 径向畸变与透镜的形状密切相关，而且离透镜中心越远的地方畸变越明显。 径向畸变大都表现为桶形畸变和枕型畸变两种方式。畸变的多项调节公式为：

其中(xi,yi)是图像平面上的理想点。(x0,y0)是畸变矫正后实际位置点。理想点与 成像中心的距离 2 2 i i r x y   ，k1，k2，k3 表示为相机径向畸变系数。如果这三个 系数都小于零，那么将造成桶型畸变；如果三个系数均都大于零，则将造成枕型 畸变。 (2) 切向畸变 切向畸变的产生大都由于整个摄像机的组装和制造过程。对于切向畸变来说， 可以使用两个切向畸变系数 p1和 p2进行纠正：

得到上述矫正公式后就可以完成对图像良好的修正。将切向矫正函数与径向 矫正函数联合起来后，可以用如下公式表示：

由于本文测距是面向自动驾驶领域，其对精度要求很高，畸变会对智能驾驶 性能造成深远的负面影响。所以在这些应用中，系统必须使用相机标定法求取 p1 和 p2以及 k1、k2和 k3，并且这些参数后续测距模型也将应用到。

相机标定流程

相机标定可以获得畸变参数和相机内外参数，相机的标定可以分为依赖于标 定参照物的标定方法和相机自标定方法两种。前者适用于对精度要求高的应用场 合。后者由于标定后的计算结果会产生较大的误差，因此不适用于对精确度要求 很高的应用场景。为了追求计算精度，本文采取第一种方法进行标定。

标定数据图像的采集

为了获得相机内外参数以及相机畸变系数，需求得世界坐标系上的点与图像 坐标系上对应点的关系。采用大小固定、易被检测、真实宽高已知的棋盘网格板 来快速方便地定位出正方形的拐角。世界坐标系可以由粘贴在一个光滑平面的棋 盘格图案来确定，三维点是棋盘格中正方形的拐角，如图 5-7 所示。Xw轴和 Yw 轴 沿平面移动，Zw轴垂直于平面移动。因此，棋盘格上的所有点都位于 X-Y 平面上， Zw 的值等于 0。为了更精准的求解参数，用摄像头拍摄了不同距离和不同角度下 15 张大小已知的棋盘格图，并且网格尺寸为 10*7、在标定过程中，通过一组已知 的三维点(Xw, Yw，Zw)及其在拍摄后图像中相应的像素位置(u，v)来计算出摄像头的 内外参数。

角点的提取

通过软件求取每个角点在图像中的对应位置。图 5-8 中，坐标原点位于图片左 上方(0,0)处， X 轴为宽度方向，Y 轴为高度方向。黄色矩形框为棋盘格的原点， 绿色圆表示找到的角点。将绿色圆表示的点的位置以及它们的真实位置对应起来， 然后就可以求解出畸变系数。

相机参数获取和图片矫正

将上图绿色圆点在图片中的位置以及它们的真实位置对应后，调用 OpenCV 中的函数来进行求解计算，获得了相机内外参数矩阵、畸变系数参数。本文采用 焦距 f，像素分辨率为 4032*3024，具体求解参数如下：

径向畸变系数=0.1457 0.2989 ，  切向畸变系数=0 0， 由上面可得像元尺寸 dx=dy=1.45um，主点坐标(u0,v0)=(1953.2,1510.5)，把畸变 系数等参数代入到畸变矫正公式后，就可以完成了对相机畸变的矫正。

单目测距模型

在完成了相机畸变矫正和相机内外参数的求取之后，建立了如下的单目测距 模型，再结合第四章目标检测获取的矩形框就可以进行距离的求取。

测距模型可以看作是一个凸透镜成像的过程。上图中，Xc-Yc-Zc是相机坐标系， xO1y是图像坐标系，O1O为焦距f，x1O2y1是地面坐标系，OO2为摄像头安装高度h。 图中有一辆车在地面上，那么其接地点Q必定在地面上。在单目测距过程中，实际 物体上的Q点在成像的图片上对应Q＇点，Q＇点在y轴上的投影为P＇点。水平线 与Zc轴的夹角为α，Zc光轴与PP＇的夹角为β，直线OP与地面x1轴的夹角为γ。

目标点的选取

根据第四章的运行结果将获得图5-11中的目标检测框，并且已知相机内外参数， 将其联合起来就可以得到测距值。具体的本文首先要选取参考点(目标点)，拟选取 目标框底部中点位置作为参考点，并根据大量目标框的获取结果。观察到目标矩 64 形框比目标物实际尺寸略大，因此采取偏移的方式对目标参考点进行矫正以保证 测距精确度。本文采取让参考点向上偏移d个像素点，并且获取的是目标框的左上 角和右下角坐标，因此参考点坐标可以表示为：

其中xL、xR、yR表示红色框的左上角x坐标、右下角x坐标、右下角y坐标。

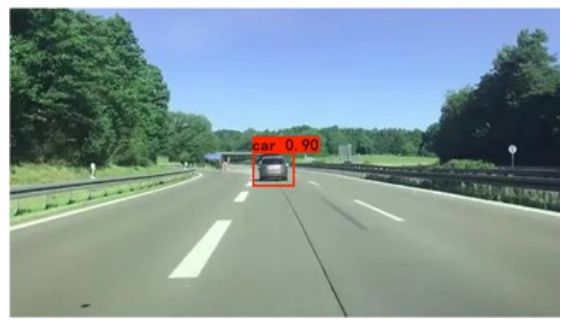
然而上述目标点适合前方物体在本车正前方的场景，当面对场景如图5-12时， 目标物会出现在本车侧方位置。如果再把目标框下部中点作为测距目标点，会出 现目标点严重偏离车辆正下方的问题，存在目标点出现在汽车中心位置左侧或中 心右侧的现象，这会造成测距精度不高的缺点。因此，进一步的对其进行改进， 当目标点(xp，yp)与图像下部中点斜率k满足阈值δ时，就会更新xp＇的值，新的xp＇ 可以表示为：

其中λ为偏移权重系数，当k值为负时，λ为负；当k值为正时，λ也为正。

距离的求取

由上面求得的内参矩阵可得fx，fy。由测距模型5-11可以推得Zc 光轴与PP＇的夹角β：

直线OP与地面x1轴的夹角γ可以看作是水平线与PP＇的夹角   = + 深度公式可以表示为：

把图像坐标点(xp,yp)转换为相机坐标系上的点可以表示为：

得到最后的距离公式为：

实验结果及分析

为了验证方法的合理性，本文将实测距离与仿真结果进行对比验证。因为目 标物的距离不同会造成预测的精度也不同，具体实验流程如下：

(1) 用棋盘网格图对车载摄像头进行标定，将棋盘格图放在摄像头前的不同距 离以及倾斜不同的角度，将采集到的17张图像导入到软件中来求解相机内外参数 以及畸变系数。

(2)采集不同距离下的车、行人等图像，并将出现在图像中的目标物利用卷尺 对其真实距离进行测量。

(3)利用矫正公式将采集到的图像进行矫正，以获得良好的测试位置。

(4)将矫正后的图像数据集输入到目标检测模型和测距模型中进行仿真测距。

添加图片注释，不超过 140 字（可选）

代码部署

环境安装与运行

pip install -r requirement.txt python detete_distance.py

重要代码

depth = (cam_H / np.sin(x)) * math.cos(angle_b)#目标深度 # print('depth', depth) ##联系--方式：----qq767172261-------- k_inv = np.linalg.inv(in_mat)#K^-1 内参矩阵的逆 p_inv = np.linalg.inv(out_mat)#R^-1 外参矩阵的逆 print("out---:",p_inv) point_C = np.array([x_d, y_d, 1]) ##图像坐标 point_A = np.transpose(point_c)#目标的世界坐标 # print('point_c', point_c） print('in----', k_inv) ##相机坐标系和图像坐标系下物体坐标可按照下式转换。

本章总结

本章完成了对目标的测距任务，首先对相机的成像原理进行描述和分析，推 导世界坐标系与图像的像素坐标系之间的关系；介绍了相机畸变的类型并给出了 矫正公式，采集图像并利用公式对相机进行内外参数的求取，完成了图像的矫正，将采集到的图像 代入到测距模型中进行验证发现，可以达到测距 要求。

联系--方式：----qq767172261----------