LibreOJ - 2874 历史研究 （回滚莫队）

回滚莫队就是在基础莫队的前提下，用更多的增加操作代替了减操作。

分成两种情况

        1、一个询问的整个区间都在一个块儿里；这种情况直接暴力求即可，因为在一个块儿里，时间复杂度不会高。

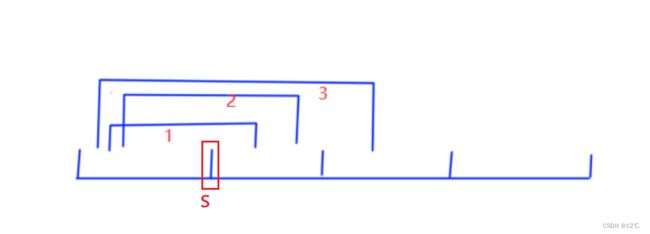
        2、一个询问的整个区间不在一个块儿里；这种情况下，在第一个块儿内的区间还是暴力处理，但是从下一个块儿开始的区间就正常的去更新，如下图情况。

          每次都是处理所有左端点都在同一个块儿的询问，按顺序处理1、2、3，在处理某个询问的时候从第一个块儿的右端点 + 1的位置s，从s向右更新到询问的右端点，记录结果值用于之后混滚到暴力处理之前的结果状态。然后从s - 1 向左暴力处理即可，得到询问整个区间的结果，在计算出来这个询问的结果的之后应该把结果回滚到暴力处理左区间之前的结果值，并且把暴力处理区间所更新的状态回滚。在计算第二个询问的时候，s 到右端点的值是从上一个询问s到右端点的结果值更新过来的。每处理完一个询问之后，只保存从第二个块儿开始到右端点的区间结果值。

#include
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define endl "\n"
//#define x first
//#define y second
//#define int long long
using namespace std;
typedef long long ll;
typedef pair pii;
typedef pair pis;
const int mod = 1e9 + 7;
const int N = 1e6+ 10;
int dx[] = {-1, 0, 1, 0, -1, 1, 1, -1};
int dy[] = {0, 1, 0, -1, 1, 1, -1, -1};
int n, m, len;
int o[N];
int w[N], cnt[N], as[N];
ll ans[N];

struct Query{ // 记录查询列表
	int id, l, r;
}q[N];
struct LSH{ // 用于离散，记录值与原来的位置。
	int a, id;	
}lsh[N];

inline int get(int x) // 得到块号
{
	return x / len;
}

bool cmp(const Query& a, const Query& b) // 基础莫队的一个排序方式
{
	int i = get(a.l), j = get(b.l);
	if(i != j) return i < j; 
	return a.r < b.r;
	
}

inline void lsh_init() // 离散化处理，原数组太大，不利于标记。
{
	stable_sort(lsh + 1, lsh + n + 1, [&](LSH a, LSH b){ // 先排序
		return a.a < b.a;
	});
	int a = 0, l = -1;
	for(int i = 1; i <= n; i ++)
	{
		if(lsh[i].a == l) o[lsh[i].id] = a; // 把离散化后的值替换原来的值
		else o[lsh[i].id] = ++ a;
		l = lsh[i].a; // 记录前一个值
		as[lsh[i].id] = l; // 记录替换前的值，用于计算之后结果
	}
}

inline void add(int a, ll& res) // 增加
{
	cnt[o[a]] ++;
	res = max(res, 1ll*cnt[o[a]] * as[a]);
}

inline void sovle()
{
	cin >> n >> m;
	len = sqrt(n);
	for(int i = 1; i <= n; i ++) {
		cin >> lsh[i].a;
		lsh[i].id = i;
	}
	lsh_init(); // 离散化处理
	for(int i = 0; i < m; i ++) // 输入询问列表
	{
		int l, r;
		cin >> l >> r;
		q[i] = {i + 1, l, r};
	}
	
	stable_sort(q, q + m, cmp); // 离线排序处理。

	for(int x = 0; x < m;)
	{
		int y = x;
		while(y < m && get(q[y].l) == get(q[x].l)) y ++; // 找到所有左端点都在当前块儿的询问
		
        int right = get(q[x].l) * len + len - 1; // 找出当前块儿的右端点
		
		// 暴力求块内的询问
		while(x < y && q[x].r <= right) // 将所有整个区间都在这个块儿内的询问暴力解决。
		{
			ll res = 0;
			int id = q[x].id, l = q[x].l, r = q[x].r;
			for(int k = l; k <= r; k ++) add(k, res);
			ans[id] = res;
			for(int k = l; k <= r; k ++) cnt[o[k]] --;
			x ++;
 		}
 		// 求块外的询问
		ll res = 0;
		int i = right, j = right + 1; // 当左端点块儿号相同的时候，是按右端点排序的，所以只需要动态的增加即可。最开始是从下一个块的第一个位置开始处理的。
		while(x < y)  // 将所有左端点在当前块儿，且右端点不在当前块儿的询问解决。
		{
			int id = q[x].id, l = q[x].l, r = q[x].r;
			while(i < r) add(++ i, res); // 处理从下一个块儿开始的区间。
			ll backup = res; // 记录当前的结果。
			while(j > l) add(-- j, res); // 暴力向左处理当前块儿的区间。
			ans[id] = res; // 记录结果
			while(j < right + 1) cnt[o[j ++]] --; // 回滚状态。
			res = backup; // 回滚暴力处理之前的结果
			x ++; // 计算下一个询问。
 		}
		memset(cnt, 0, sizeof cnt); // 清空标记数组。
	}
	for(int i = 1; i <= m; i ++) cout << ans[i] << endl; // 输出结果

}
signed main(void)
{
	IOS;
	int t = 1;
//	cin >> t;
	while(t --) sovle();
	return 0;
}