【深度学习笔记】6.循环神经网络
循环神经网络
计算图
计算图的引入是为了后面更方便的表示网络,计算图是描述计算结构的一种图,它的元素包括节点(node)和边(edge),节点表示变量,可以是标量、矢量、张量等,而边表示的是某个操作,即函数。
下面这个计算图表示复合函数
关于计算图的求导,我们可以用链式法则表示,有下面两种情况。
- 情况1
- 情况2
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SUose3jf-1638344566342)(https://datawhalechina.github.io/unusual-deep-learning/PIC/6/6.4.png)]
求导举例
例1
假设a = 3, b = 1 可以得到 c = 3, d = 2, e = 6
∂ e ∂ a = ∂ e ∂ c ∂ c ∂ a = d = b + 1 = 2 ∂ e ∂ b = ∂ e ∂ c ∂ c ∂ b + ∂ e ∂ d ∂ d ∂ b = d + c = b + 1 + a + b = 5 \frac{\partial e}{\partial a}=\frac{\partial e}{\partial c}\frac{\partial c}{\partial a}=d=b+1=2 \\ \frac{\partial e}{\partial b}=\frac{\partial e}{\partial c}\frac{\partial c}{\partial b} + \frac{\partial e}{\partial d}\frac{\partial d}{\partial b}=d+c=b+1+a+b=5 ∂a∂e=∂c∂e∂a∂c=d=b+1=2∂b∂e=∂c∂e∂b∂c+∂d∂e∂b∂d=d+c=b+1+a+b=5
例2

∂ Z ∂ X = α δ + α ϵ + α ζ + β δ + β ϵ + β ζ + γ δ + γ ϵ + γ ζ = ( α + β + γ ) ( δ + ϵ + ζ ) \frac{\partial Z}{\partial X}=αδ+αϵ+αζ+βδ+βϵ+βζ+γδ+γϵ+γζ=(α+β+γ)(δ+ϵ+ζ) ∂X∂Z=αδ+αϵ+αζ+βδ+βϵ+βζ+γδ+γϵ+γζ=(α+β+γ)(δ+ϵ+ζ)
计算图可以很好的表示导数的前向传递和后向传递的过程 。
。
循环神经网络
现实生活中存在很多序列化结构,我们需要建立一种更优秀的序列数据模型。比如:
- 文本:字母和词汇的序列
- 语音:音节的序列
- 视频:图像帧的序列
- 时态数据:气象观测数据,股票交易数据、房价数据等
基于这种大前提下,就会出现循环神经网络(RNN)。循环神经网络是一种人工神经网络,它的节点间的连接形成一个遵循时间序列的有向图,它的核心思想是,样本间存在顺序关系,每个样本和它之前的样本存在关联。通过神经网络在时序上的展开,我们能够找到样本之间的序列相关性。
结构如下:
在神经网络图里面,输入到输出要么从左到右,要么从下到上。而循环神经网络通常会采用下到上的形式来展示。
-
其中下表带t的变量代表着上一个、当前、下一个等时间单位
-
U、V、W代表着网络权重
-
b代表网络偏置
-
\omega 和 \phi代表着激活函数。通常\omega选用tanh或sigmiod,而\phi选用softmax
其中 softmax 函数,用于分类问题的概率计算。本质上是将一个K维的任意实数向量压缩 (映射)成另一个K维的实数向量,其中向量中的每个元素取值都介于(0,1)之间。
RNN案例
比如词性标注,
- 我/n,爱/v购物/n,
- 我/n在/pre华联/n购物/v
Word Embedding:自然语言处理(NLP)中的 一组语言建模和特征学习技术的统称,其中来自词汇表的单词或短语被映射到实数的向量。比如这里映射到三个向量然后输入:
将神经元的输出存到memory中,memory中值会作为下一时刻的输入。在最开始时刻,给定 memory初始值,然后逐次更新memory中的值。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5vm3FOjK-1638344566346)(https://datawhalechina.github.io/unusual-deep-learning/PIC/6/6.13.png)]
RNN一般结构
Elman Network
Jordan Network
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XLdMOdmJ-1638344566346)(https://datawhalechina.github.io/unusual-deep-learning/PIC/6/6.15.png)]
其他结构
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XELLshkb-1638344566347)(https://datawhalechina.github.io/unusual-deep-learning/PIC/6/6.16.png)]
RNN训练算法 - BPTT
我们先来回顾一下BP算法,就是定义损失函数 Loss 来表示网络输出与实际输出的误差,通过链式法则自顶向下求得 Loss 对网络权重的偏导。沿梯度的反方向更新权重的值, 直到 Loss 收敛。而这里的 BPTT 算法就是加上了时序演化,后面的两个字母 TT 就是 Through Time。
假设我们定义输出函数
s t = t a n h ( U x t + W s t − 1 ) y ^ = s o f t m a x ( V s t ) s_t=tanh(Ux_t+Ws_{t-1}) \\ \widehat{y}=softmax(Vs_t) st=tanh(Uxt+Wst−1)y =softmax(Vst)
再定义损失函数
E t ( y t , y ^ t ) = − y t l o g ( y ^ t ) E ( y t , y ^ t ) = ∑ t E t ( y t , y ^ t ) = − ∑ t y t l o g ( y ^ t ) E_t(y_t,\widehat{y}_t)=-y_tlog(\widehat{y}_t) \\ E(y_t,\widehat{y}_t)=\sum_tE_t(y_t,\widehat{y}_t) \\ =-\sum_ty_tlog(\widehat{y}_t) Et(yt,y t)=−ytlog(y t)E(yt,y t)=t∑Et(yt,y t)=−t∑ytlog(y t)
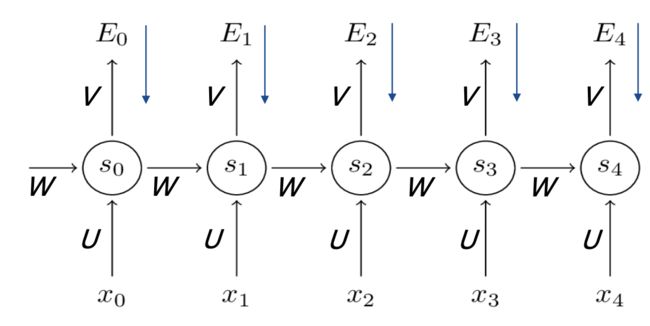
我们分别求损失函数 E 对 U、V、W的梯度:
∂ E ∂ V = ∑ t ∂ E t ∂ V ∂ E ∂ U = ∑ t ∂ E t ∂ U ∂ E ∂ W = ∑ t ∂ E t ∂ W \frac{\partial E}{\partial V}=\sum_t\frac{\partial E_t}{\partial V} \\ \frac{\partial E}{\partial U}=\sum_t\frac{\partial E_t}{\partial U} \\ \frac{\partial E}{\partial W}=\sum_t\frac{\partial E_t}{\partial W} ∂V∂E=t∑∂V∂Et∂U∂E=t∑∂U∂Et∂W∂E=t∑∂W∂Et
- 求 E 对 V 的梯度,先求 E_3对 V 的梯度
∂ E 3 ∂ V = ∂ E 3 ∂ y ^ 3 ∂ y ^ 3 ∂ V = ∂ E 3 ∂ y ^ 3 ∂ y ^ 3 ∂ z 3 ∂ z 3 ∂ V \frac{\partial E_3}{\partial V}=\frac{\partial E_3}{\partial \widehat{y}_3}\frac{\partial \widehat{y}_3}{\partial V}\\ =\frac{\partial E_3}{\partial \widehat{y}_3}\frac{\partial \widehat{y}_3}{\partial z_3}\frac{\partial z_3}{\partial V} ∂V∂E3=∂y 3∂E3∂V∂y 3=∂y 3∂E3∂z3∂y 3∂V∂z3
其中z_3=V_s_3,然后求和即可。
- 求E对W的梯度,先求E_3对W的梯度
∂ E 3 ∂ W = ∂ E 3 ∂ y ^ 3 ∂ y ^ 3 ∂ s 3 ∂ s 3 ∂ W S 3 = t a n h ( U x 3 + W s 2 ) ∂ E 3 ∂ W = ∑ k = 0 3 ∂ E 3 ∂ y ^ 3 ∂ y ^ 3 ∂ s 3 ∂ s 3 ∂ s k ∂ s k ∂ W ∂ E 3 ∂ W = ∑ k = 0 3 ∂ E 3 ∂ y ^ 3 ∂ y ^ 3 ∂ s 3 ( ∏ j = k + 1 3 ∂ s j ∂ s j − 1 ) ∂ s k ∂ W \frac{\partial E_3}{\partial W}=\frac{\partial E_3}{\partial \widehat{y}_3}\frac{\partial \widehat{y}_3}{\partial s_3}\frac{\partial s_3}{\partial W}\\ S_3=tanh(Ux_3+Ws_2)\\ \frac{\partial E_3}{\partial W}=\sum_{k=0}^{3}\frac{\partial E_3}{\partial \widehat{y}_3}\frac{\partial \widehat{y}_3}{\partial s_3}\frac{\partial s_3}{\partial s_k}\frac{\partial s_k}{\partial W}\\ \frac{\partial E_3}{\partial W}=\sum_{k=0}^{3}\frac{\partial E_3}{\partial \widehat{y}_3}\frac{\partial \widehat{y}_3}{\partial s_3}(\prod_{j=k+1}^{3} \frac{\partial s_j}{\partial s_{j-1}})\frac{\partial s_k}{\partial W} ∂W∂E3=∂y 3∂E3∂s3∂y 3∂W∂s3S3=tanh(Ux3+Ws2)∂W∂E3=k=0∑3∂y 3∂E3∂s3∂y 3∂sk∂s3∂W∂sk∂W∂E3=k=0∑3∂y 3∂E3∂s3∂y 3(j=k+1∏3∂sj−1∂sj)∂W∂sk
其中:s_3依赖于s_2,而s_2又依赖与s_1和W,依赖关系一致传递到t=0的时刻。因此我们计算对于W的偏导时,不能把s_2看作时常数项
- 求E对U的梯度,先求E_3对U的梯度
∂ E 3 ∂ U = ∂ E 3 ∂ y ^ 3 ∂ y ^ 3 ∂ s 3 ∂ s 3 ∂ U S 3 = t a n h ( U x 3 + W s 2 ) ∂ E 3 ∂ U = ∑ k = 0 3 ∂ E 3 ∂ y ^ 3 ∂ y ^ 3 ∂ s 3 ∂ s 3 ∂ s k ∂ s k ∂ U \frac{\partial E_3}{\partial U}=\frac{\partial E_3}{\partial \widehat{y}_3}\frac{\partial \widehat{y}_3}{\partial s_3}\frac{\partial s_3}{\partial U}\\ S_3=tanh(Ux_3+Ws_2)\\ \frac{\partial E_3}{\partial U}=\sum_{k=0}^{3}\frac{\partial E_3}{\partial \widehat{y}_3}\frac{\partial \widehat{y}_3}{\partial s_3}\frac{\partial s_3}{\partial s_k}\frac{\partial s_k}{\partial U} ∂U∂E3=∂y 3∂E3∂s3∂y 3∂U∂s3S3=tanh(Ux3+Ws2)∂U∂E3=k=0∑3∂y 3∂E3∂s3∂y 3∂sk∂s3∂U∂sk
长短时记忆网络
在RNN中,存在一个很重要的问题,就是梯度消失问题,一开始我们不能有效的解决长时依赖问题,其中梯度消失的原因有两个:BPTT算法和激活函数Tanh。
为了解决这两种问题,后续提出了两个解决方案
- 使用ReLU函数代替Tanh
- 使用门控RNN来空值是否记忆,其中出名的就有LSTM和GRU
LSTM
LSTM,及长短时记忆网络,属于RNN的范畴。它的核心思想就是提出门控的概念,通过门口决定当前时刻是否需要记忆上一时刻的结果。一个LSTM单元由输入门、输出门和遗忘门组成,三个门控制信息进出单元。
- LSTM依靠贯穿隐藏层的细胞状态实现隐藏单元之间的信息传递,其中只有少量的线性操作
- LSTM引入了“门”机制对细胞状态信息进行添加或删除,由此实现长程记忆
- “门”机制由一个Sigmoid激活函数层和一个向量点乘操作组成,Sigmoid层的输出控制了信息传递的比例
遗忘门:LSTM通过遗忘门(forget gate)实现对细胞状态信息遗忘程度的控制,输出当前状态的遗忘权重,取决于 h_{t-1}和x_t
f t = σ ( W f ⋅ [ h t − 1 , x t ] + b f ) f_t=\sigma(W_f·[h_{t-1},x_t]+b_f) ft=σ(Wf⋅[ht−1,xt]+bf)

输入门:LSTM通过输入门(input gate)实现对细胞状态输入接收程度的控制,输出当前输入信息的接受权重,取决于h_{t-1}和x_t
i t = σ ( W i ⋅ [ h t − 1 , x t ] + b i ) C t = t a n h ( W C ⋅ [ h t − 1 , x t ] + b C ) i_t=\sigma(W_i·[h_t-1,x_t]+b_i)\\ C_t=tanh(W_C·[h_t-1,x_t]+b_C) it=σ(Wi⋅[ht−1,xt]+bi)Ct=tanh(WC⋅[ht−1,xt]+bC)

输出门:LSTM通过输出门(output gate)实现对细胞状态输出认可程度的控制,输出当前输出信息的认可权重,取决于h_{t-1}和x_t
o t = σ ( W o ⋅ [ h t − 1 , x t ] + b o ) o_t=\sigma(W_o·[h_{t-1},x_t]+b_o) ot=σ(Wo⋅[ht−1,xt]+bo)

状态更新:“门”机制对细胞状态信息进行添加或删除,由此实现长程记忆。
C t = f t ∗ C t − 1 + i t ∗ C ~ t h t = o t ∗ t a n h ( C t ) C_t=f_t*C_{t-1}+i_t*\widetilde{C}_t \\ h_t=o_t*tanh(C_t) Ct=ft∗Ct−1+it∗C tht=ot∗tanh(Ct)
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hZ0lqMMd-1638344566350)(https://datawhalechina.github.io/unusual-deep-learning/PIC/6/6.24.png)]
下面给出一个标准化的RNN例子
#构造RNN网络,x的维度5,隐层的维度10,网络的层数2
rnn_ seq = nn.RNN(5, 10,2)
#构造一个输入序列,长为6,batch是3,特征是5
X =V(torch. randn(6, 3,5))
#out,ht = rnn_ seq(x, h0) # h0可以指定或者不指定
out,ht = rnn_ seq(x)
# q1:这里out、ht的size是多少呢? out:6*3*10, ht:2*3*10
#输入维度50,隐层100维,两层
Lstm_ seq = nn.LSTM(50, 100,num layers=2 )
#输入序列seq= 10,batch =3,输入维度=50
lstm input = torch. randn(10,3,50)
out, (h, c) = lstm_ seq(lstm_ _input) #使用默认的全0隐藏状态
GRU
GRU可以认为是LSTM的变种,本质上也是通过门控来空值网络的记忆能力。但在计算当前时刻新信息的方法和LSTM有 所不同;GRU只包含重置门和更新门;在音乐建模与语音信号建模领域与LSTM具有相似的性能,但是参数更少,只有两个门控。
所以一般情况下,GRU的计算量比LSTM要小,而准确性就要视具体问题及数据而定。
其他经典的循环神经网络
Peephole LSTM
让门层也接受细胞状态的输入,同时考虑隐层信息的输入。
Bi-directional RNN(双向RNN)
Bi-directional RNN(双向RNN)假设当前t的输出不仅仅和之前的序列有关,并且还与之后的序列有关,例如:完形填空,它由两个RNNs上下叠加在一起组成,输出由这两个RNNs的隐藏层的状态决定。
Continuous time RNN(CTRNN)
CTRNN利用常微分方程系统对输入脉冲序列神经元的影响 进行建模。CTRNN被应用到进化机器人中,用于解决视觉、协作和最 小认知行为等问题。
循环神经网络的主要应用
语音模型
根据之前和当前词预测下一个单词或者字母
问答系统
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nTEyMIm5-1638344566352)(https://datawhalechina.github.io/unusual-deep-learning/PIC/6/6.30.png)]
自动作曲
Music AI Lab: https://musicai.citi.sinica.edu.tw/
机器翻译
将一种语言自动翻译成另一种语言
自动写作
根据现有资料自动写作,当前主要包括新闻写作和诗歌创作。主要是基于RNN&LSTM的文本生成技术来实现,需要训练大量同 类文本,结合模板技术。
目前主要产品有:腾讯Dreamwriter写稿机器人、今日头条xiaomingbot、第一财经DT稿王(背后是阿里巴巴) 、百度Writing-bots等
图像描述
根据图像形成语言描述
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZG1CJX3m-1638344566355)(https://datawhalechina.github.io/unusual-deep-learning/PIC/6/6.34.png)]
参考资料:datawhale



















