《动手学深度学习》4.5. 权重衰减(李沐)
4.5.1. 高维线性回归
代码学习笔记(含详细注释)
通过一个简单的例子来演示权重衰减
4.5.1. 高维线性回归
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
若在pycharm上面用到matplotlib库,可以将上述代码中的:%matplotlib inline
替换为:import matplotlib.pyplot as plt 然后在需要输出图像的地方加上 plt.show()
生成公式如下:
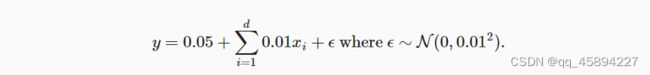
我们选择标签是关于输入的线性函数。 标签同时被均值为0,标准差为0.01高斯噪声破坏。 为了使过拟合的效果更加明显,我们可以将问题的维数增加到d=200, 并使用一个只包含20个样本的小训练集。
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
# 赋真实值,true_b=0.05,所有true_w=0.0100
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
# 调用d2l库中的synthetic_data构造一个数据集
# 生成 y=X*true_w+true_b+noise
train_data = d2l.synthetic_data(true_w, true_b, n_train)
# 读取数据 调用d2l库中的一个数据迭代器 每次只选取batch_size规模的数据
train_iter = d2l.load_array(train_data, batch_size)
# 原理同上
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)
4.5.2. 从零开始实现
从头开始实现权重衰减,只需将L2的平方惩罚添加到原始目标函数中。
4.5.2.1. 初始化模型参数
# 初始化模型参数
def init_params():
w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
return [w, b]
4.5.2.2. 定义L2范数惩罚
def l2_penalty(w):
# 对w中每一项都求平方,然后相加求平方和,再除以2
return torch.sum(w.pow(2)) / 2
扩展:
pow(x,y):表示x的y次幂。
pow(x,y,z):表示x的y次幂后除以z的余数。
4.5.2.3. 定义训练代码实现
将模型拟合训练数据集,并在测试数据集上进行评估。
def train(lambd):
# 对参数赋值
w, b = init_params()
# lambda为匿名函数
# 举个例子:f = lambda x: x*2+1
# f(3)=7
# 此段代码通过调用d2l.linreg(X, w, b)简单设置了一个线性net
# net(X)==d2l.linreg(X, w, b)
net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
num_epochs, lr = 100, 0.003
# 绘图函数
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend= ['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
# 增加了L2范数惩罚项,
# 广播机制使L2_penalty(w)成为一个长度为batch_size的向量
l = loss(net(X), y) + lambd * l2_penalty(w)
l.sum().backward()
d2l.sgd([w, b], lr, batch_size)
# 每5个epoch更新一次图表
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
# 取出单元素张量的元素值并返回该值,保持原元素类型不变
# item()返回的是一个数
# torch.norm(w)求其L2范式
print('w的L2范数是:', torch.norm(w).item())
4.5.2.4. 忽略正则化直接训练
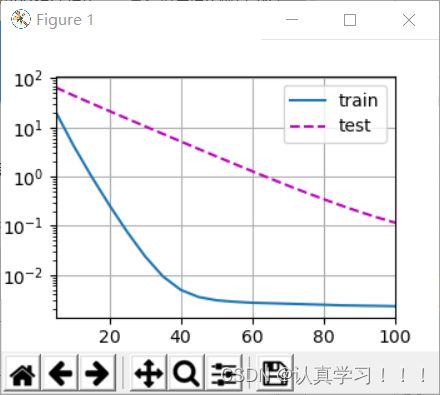
我们现在用lambd = 0禁用权重衰减后运行这个代码。 注意,这里训练误差有了减少,但测试误差没有减少, 这意味着出现了严重的过拟合。
train(lambd=0)
运行结果:
![]()

4.5.2.5. 使用权重衰减
下面,我们使用权重衰减来运行代码。 注意,在这里训练误差增大,但测试误差减小。 这正是我们期望从正则化中得到的效果。
train(lambd=3)
4.5.3. 简洁实现
由于权重衰减在神经网络优化中很常用, 深度学习框架为了便于我们使用权重衰减, 将权重衰减集成到优化算法中,以便与任何损失函数结合使用。 此外,这种集成还有计算上的好处, 允许在不增加任何额外的计算开销的情况下向算法中添加权重衰减。 由于更新的权重衰减部分仅依赖于每个参数的当前值, 因此优化器必须至少接触每个参数一次。
在下面的代码中,我们在实例化优化器时直接通过weight_decay指定weight decay超参数。 默认情况下,PyTorch同时衰减权重和偏移。 这里我们只为权重设置了weight_decay,所以偏置参数b不会衰减。
def train_concise(wd):
net = nn.Sequential(nn.Linear(num_inputs, 1))
# 随机初始化网络的参数
for param in net.parameters():
param.data.normal_()
loss = nn.MSELoss(reduction='none')
num_epochs, lr = 100, 0.003
# 直接在优化器内实现权重衰减
# 偏置参数没有衰减
trainer = torch.optim.SGD([
{"params":net[0].weight,'weight_decay': wd},
{"params":net[0].bias}], lr=lr)
# 画图函数
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
trainer.zero_grad()
l = loss(net(X), y)
l.mean().backward()
trainer.step()
# 每五次epoch更新一次图像
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1,
(d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
print('w的L2范数:', net[0].weight.norm().item())
这些图看起来和我们从零开始实现权重衰减时的图相同。 然而,它们运行得更快,更容易实现。 对于更复杂的问题,这一好处将变得更加明显。
忽略正则化直接训练:
train_concise(0)
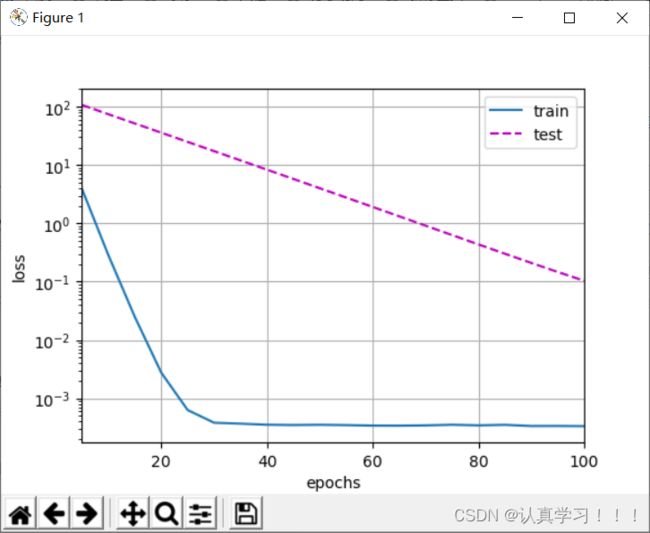
使用权重衰减:
train_concise(3)
运行结果:
![]()
4.5.4. 小结
1.正则化是处理过拟合的常用方法:在训练集的损失函数中加入惩罚项,以降低学习到的模型的复杂度。
2.保持模型简单的一个特别的选择是使用L2惩罚的权重衰减。这会导致学习算法更新步骤中的权重衰减。
3.权重衰减功能在深度学习框架的优化器中提供。
4.在同一训练代码实现中,不同的参数集可以有不同的更新行为。
参考文献:
《动手学深度学习》