【精读文献】1 用于改进脑电图癫痫分析的自监督图神经网络
一、方法概述
1、摘要
从脑电图中自动检测和分类癫痫可以极大地改善癫痫的诊断和治疗。然而,在先前的自动癫痫检测和分类研究中,有几个建模挑战仍未得到解决:(1)表示脑电图中的非欧几里得数据结构,(2)准确分类罕见的癫痫类型,以及(3)缺乏定量可解释性方法来衡量模型定位癫痫的能力。
在这项研究中,我们通过以下方式来应对这些挑战:(1)使用图神经网络(GNN)表示脑电图中的时空依赖性,并提出两种捕捉电极几何形状或动态大脑连接的脑电图图结构;(2)提出一种自监督预训练方法,预测下一时间段的预处理信号,以进一步提高模型性能,特别是在罕见的癫痫发作类型上,以及(3)提出一种定量模型可解释性方法来评估模型在脑电图中定位癫痫发作的能力。
当在大型公共数据集(5499个脑电图)上评估我们的癫痫检测和分类方法时,我们发现我们的自我监督预训练GNN在癫痫检测上达到了0.875的受试者操作特征曲线下面积,在癫痫分类上达到了0.749的加权F1分,在癫痫检测和归类方面都优于以前的方法。此外,我们的自我监督预训练策略显著改善了罕见癫痫发作类型的分类(例如,与基线相比,联合强直性癫痫发作的准确性提高了47分)。此外,定量可解释性分析表明,我们的自我监督预训练的GNN精确定位了25.4%的局灶性癫痫发作,比现有的CNN提高了21.9个百分点。最后,通过将识别的癫痫发作位置叠加在原始脑电图信号和脑电图图上,我们的方法可以为临床医生提供局部癫痫发作区域的直观可视化。
2、方法
二、原始数据
Temple University Seizure Corpus (TUSZ) v1.5.2
Temple University Hospital 公开的癫痫发作EEG库,作为基础数据,是目前最大的公共EEG数据库。
其中包含5612条癫痫EEG信号,3050条注解的癫痫诊断记录,8种癫痫种类。采用的标准10-20系统,每个EEG包含19个通道(电极)。

三、数据集构建
- step 1 resampling
将Train Set分为训练和验证
首先对所有数据进行重采样,重采样至200Hz。
- 癫痫检测:使用无重叠,长为t(12s/60s)的滑动窗口从EEG信号片段中截取片段,对于癫痫的片段,设值标签y=1,对于正常的脑电片段,设值标签y=0。如果最后一个窗口短于片段长度,则忽略它。
- 癫痫分类:只采用癫痫发作的脑电图,从每个癫痫事件中获取一个12s(60s)的EEG片段,发作结束即截止,每个脑电片段就有一个对应的癫痫类型。从注释的癫痫发作时间前的2秒开始,其中2秒的偏移说明了注释中的容差。重新定义癫痫类型为四类,Label Y={1,2,3,4} 。其对应于局灶性(CF)合并癫痫发作、广义非特异性(GN)癫痫发作、缺席(AB)癫痫发作和强直性(CT)联合癫痫发作。
- 自监督预训练:使用12秒(60s)的滑动窗口获取EEG信号片段(与癫痫检测相同)。学习预测下一个时间段的EEG信号,使用真实预处理的EEG片段和预测片段(T=12s)之间的平均绝对误差作为损失函数。
For each EEG clip in each of seizure detection/seizure classification / self-supervised pretaining tasks,执行以下预处理步骤:
- step 2 滑窗
在脑电片段上滑动 t 秒窗口,不重叠,其中 t 是涉及递归层的网络的时间步长;
- step 3 FFT
使用Scipy python包中的“FFT”函数对每个 t 秒窗口应用快速傅立叶变换(fast Fourier transform,FFT)(Virtanen等人,2020b),并保留非负频率分量的对数振幅,类似于先前的研究(Asif等人,2020;Ahmedt-Aristizabal等人,2020年;Covert等人,2019)
- step 4 归一化
相对于训练数据的平均值和标准偏差对EEG片段进行z归一化(z-normalize)
归一化步骤:
1.求出各变量(指标)的算术平均值(数学期望)xi和标准差si ;
2.进行标准化处理:
zij=(xij-xi)/si
其中:zij为标准化后的变量值;xij为实际变量值。
3.将逆指标前的正负号对调。
标准化后的变量值围绕0上下波动,大于0说明高于平均水平,小于0说明低于平均水平。
def z_score(x, axis):
x = np.array(x).astype(float)
xr = np.rollaxis(x, axis=axis)
# 减去均值
xr -= np.mean(x, axis=axis)
# 除以标准差
xr /= np.std(x, axis=axis)
# print(x)
# 完成归一化
return x
由于癫痫发作分类的EEG片段可能由于癫痫发作时间短而具有可变的长度,因此我们将片段填充为0,以便于批量进行模型训练(facilitate model training in batches)。我们使用 t=1 秒作为时间步长的自然选择。
预处理后,每个脑电片段可以表示为 X ∈ R T × N × M X∈R^{T×N×M} X∈RT×N×M,其中T=12(或T=60)表示片段clip长度,N=19表示脑电通道/电极的数量,M=100表示上述傅立叶变换后的特征维数。
四、模型训练过程和超参数的详细信息
在验证集上进行超参数搜索:
(a)initial learning rate初始学习率范围:[5e5,1e3]
(b)correlation graphs中每个节点(node)要保持的邻点数量: τ ∈ 2 , 3 , 4 \tau \in {2,3,4} τ∈2,3,4
(c)DCGRU的层数 :{2,3,4,5},隐藏单元范围:{32,64,128}
(d)最大扩散步长(max diffusion step)K∈{2,3,4}
(e) 最后一个完全连接层中的丢失概率dropout probability。
1、癫痫发作检测模型训练
undersample 使得训练集正负样本比例约为1:1
27,292 training examples for 12-s clips and 7,188 training examples for 60-s clips
损失函数:binary cross-entropy,二元交叉熵
initia learning rate : 1e-4
epoch:100
maxnum number of diffusion step:2
the dropout probability was 0 (i.e. no dropout)
该模型由两个堆叠的DCGRU层组成,具有64个隐藏单元,产生168641个距离图的可训练参数和280769个相关图的可训练参数
用于癫痫检测的模型训练对于12秒的EEG片段约20分钟,对于60秒的EEG片段约30分钟。
在验证集进行决策阈值搜索(平衡precision 和 recall scores)。决策阈值选择:in the highest F1-score on the validation set
相关指标计算:https://blog.csdn.net/qq_14997473/article/details/82684300

当评估测试集上的模型时,概率高于该决策阈值的EEG片段被预测为癫痫发作,而概率低于该决策阈值则被预测为非癫痫发作。
2、癫痫分类模型训练
损失函数:multi-class crossentropy 多类交叉熵
初始学习率:3e-4
epoch:60
对于相关性图,为每个节点保留前3个邻居的边。
扩散步骤的最大数量(maximum number of diffusion step)为2,并且脱落概率(dropout probability)为0.5。
结构:该模型由两个具有64个隐藏单元的堆叠DCGRU层组成,得到距离图的168836个可训练参数和相关图的280964个可训练的参数。
训练时间:癫痫分类的模型训练对于12秒的EEG片段大约需要3分钟,对于60秒的EEG片段大约需要7分钟。
3、自监督任务(self-supervised task)模型训练
我们假设,通过学习预测下一个时间段的EEG信号并改进下游癫痫检测和分类任务。自监督预训练的模型是一个序列到序列的结构,其中包括了一个编码器和一个解码器,每个编码器和解码器都有几个堆叠的DCGRU(图1d)。
初步实验表明,给定先前12-s(60-s)的预处理片段,在验证集上预测未来 T ′ = 12 T'=12 T′=12秒的预处理EEG片段会得到低回归损失( low regression loss),因此在所有自监督的预训练实验中使用 T ′ = 12 T'=12 T′=12。
最佳EEG clip : T ′ = 12 s T'=12s T′=12s
损失函数:mean absolute error (MAE) ,平均绝对误差
初始学习率:5e-4
epoch:350
对于相关性图,为每个节点保留前3个邻居的边。
扩散步骤的最大数量为2。
结构:该模型由三个堆叠的DCGRU层组成,在编码器和解码器中都有64个隐藏单元,产生了417572个距离图的可训练参数和690980个相关图的可训练参数。
训练时间:自我监督预测的模型训练对于12秒的EEG片段大约需要10小时,对于60秒的EEF片段大约需要24小时。
4、baselines的模型训练
五、模型训练代码实现
1、癫痫检测模型
(1)首先导入外部参数 python train.py
--input_dir <resampled-dir> --raw_data_dir <tusz-data-dir> --save_dir <save-dir> --graph_type combined --max_seq_len <clip-len> --do_train --num_epochs 100 --task detection --metric_name auroc --use_fft --lr_init 1e-4 --num_rnn_layers 2 --rnn_units 64 --max_diffusion_step 2 --num_classes 1 --data_augment
To use correlation-based EEG graph, specify --graph_type individual.
To use preprocessed Fourier transformed inputs from the above optional preprocessing step, specify --preproc_dir .
(2)Built dataset
得到:
dataloaders: dictionary of train/dev/test dataloaders
scaler: standard scaler 归一化
dataloaders, _, scaler = load_dataset_detection(input_dir=args.input_dir,
raw_data_dir=args.raw_data_dir,
train_batch_size=args.train_batch_size,
test_batch_size=args.test_batch_size,
time_step_size=args.time_step_size,
max_seq_len=args.max_seq_len,
standardize=True,
# 指定了num_workers = 8
num_workers=args.num_workers,
augmentation=args.data_augment,
adj_mat_dir='./data/electrode_graph/adj_mx_3d.pkl',
graph_type=args.graph_type,
top_k=args.top_k,
filter_type=args.filter_type,
use_fft=args.use_fft,
sampling_ratio=1,
seed=123,
preproc_dir=args.preproc_dir)
load_dataset_detection模块
def load_dataset_detection(
input_dir,
raw_data_dir,
train_batch_size,
test_batch_size=None,
time_step_size=1,
max_seq_len=60,
standardize=True,
num_workers=8,
augmentation=False,
adj_mat_dir=None,
graph_type=None,
top_k=None,
filter_type='laplacian', # 拉普拉斯算子
use_fft=False,
sampling_ratio=1,
seed=123,
preproc_dir=None):
(3)Built model
模型定义
model = DCRNNModel_classification(args=args, num_classes=args.num_classes, device=device)
将模型加载到指定设备上
# 将模型加载到指定设备上
model = model.to(device)
训练模型
# Train
train(model, dataloaders, args, device, args.save_dir, log, tbx)
训练完成后加载最优模型
# Load best model after training finished
best_path = os.path.join(args.save_dir, 'best.pth.tar')
model = utils.load_model_checkpoint(best_path, model)
# 将模型加载到指定设备上
model = model.to(device)
DCRNN模型
class DCRNNModel_classification(nn.Module):
def __init__(self, args, num_classes, device=None):
super(DCRNNModel_classification, self).__init__()
num_nodes = args.num_nodes
num_rnn_layers = args.num_rnn_layers
rnn_units = args.rnn_units
enc_input_dim = args.input_dim
max_diffusion_step = args.max_diffusion_step
self.num_nodes = num_nodes
self.num_rnn_layers = num_rnn_layers
self.rnn_units = rnn_units
self._device = device
self.num_classes = num_classes
self.encoder = DCRNNEncoder(input_dim=enc_input_dim,
max_diffusion_step=max_diffusion_step,
hid_dim=rnn_units, num_nodes=num_nodes,
num_rnn_layers=num_rnn_layers,
dcgru_activation=args.dcgru_activation,
filter_type=args.filter_type)
self.fc = nn.Linear(rnn_units, num_classes)
self.dropout = nn.Dropout(args.dropout)
self.relu = nn.ReLU()
def forward(self, input_seq, seq_lengths, supports):
"""
Args:
input_seq: input sequence, shape (batch, seq_len, num_nodes, input_dim)
seq_lengths: actual seq lengths w/o padding, shape (batch,)
supports: list of supports from laplacian or dual_random_walk filters
Returns:
pool_logits: logits from last FC layer (before sigmoid/softmax)
"""
batch_size, max_seq_len = input_seq.shape[0], input_seq.shape[1]
# (max_seq_len, batch, num_nodes, input_dim)
input_seq = torch.transpose(input_seq, dim0=0, dim1=1)
# initialize the hidden state of the encoder
init_hidden_state = self.encoder.init_hidden(
batch_size).to(self._device)
# last hidden state of the encoder is the context
# (max_seq_len, batch, rnn_units*num_nodes)
_, final_hidden = self.encoder(input_seq, init_hidden_state, supports)
# (batch_size, max_seq_len, rnn_units*num_nodes)
output = torch.transpose(final_hidden, dim0=0, dim1=1)
# extract last relevant output
last_out = utils.last_relevant_pytorch(
output, seq_lengths, batch_first=True) # (batch_size, rnn_units*num_nodes)
# (batch_size, num_nodes, rnn_units)
last_out = last_out.view(batch_size, self.num_nodes, self.rnn_units)
last_out = last_out.to(self._device)
# final FC layer
logits = self.fc(self.relu(self.dropout(last_out)))
# max-pooling over nodes
pool_logits, _ = torch.max(logits, dim=1) # (batch_size, num_classes)
return pool_logits
训练模型
def train(model, dataloaders, args, device, save_dir, log, tbx):
(4)Evaluate on dev and test set
验证集:
dev_results = evaluate(model,dataloaders['dev'], args,args.save_dir,device,
is_test=True,nll_meter=None, eval_set='dev')
# 结果
dev_results_str = ', '.join('{}: {:.3f}'.format(k, v)
for k, v in dev_results.items())
log.info('DEV set prediction results: {}'.format(dev_results_str))
测试集:
test_results = evaluate(model,
dataloaders['test'],
args,
args.save_dir,
device,
is_test=True,
nll_meter=None,
eval_set='test',
best_thresh=dev_results['best_thresh'])
# Log to console
test_results_str = ', '.join('{}: {:.3f}'.format(k, v)
for k, v in test_results.items())
log.info('TEST set prediction results: {}'.format(test_results_str))
2、自监督任务
六、实验结果
表2 癫痫发作检测和癫痫发作分类结果。平均值和标准偏差来自五次随机运行。最佳非预训练和预训练平均结果以粗体突出显示。
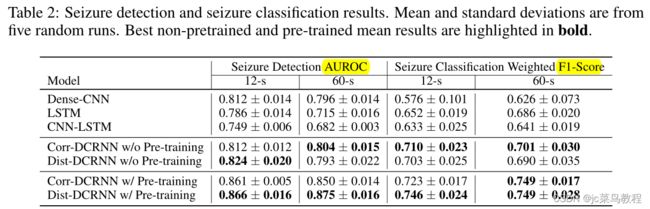
加上预训练之后,在12s的EEG clip上基于距离图构建的DCRNN模型效果较好
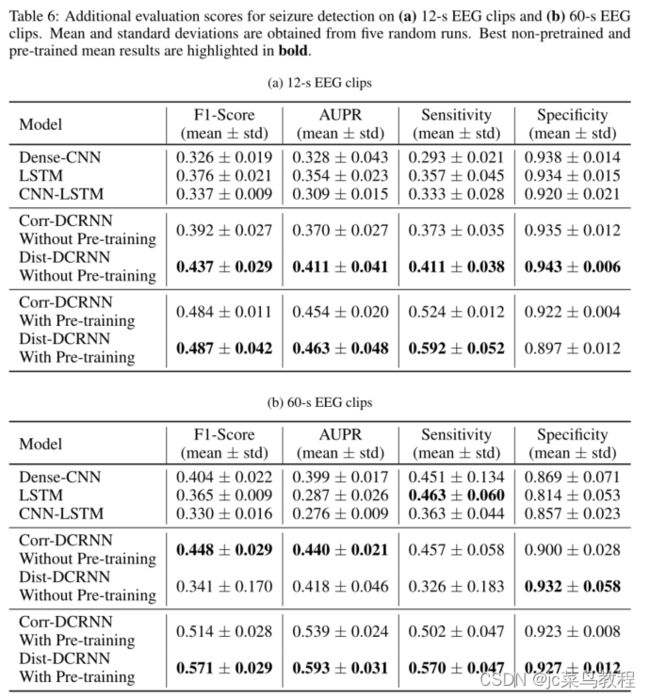
表6 癫痫检测的附加评估分数