一文秒懂迪克斯特拉Dijkstra算法

• 最短路径问题

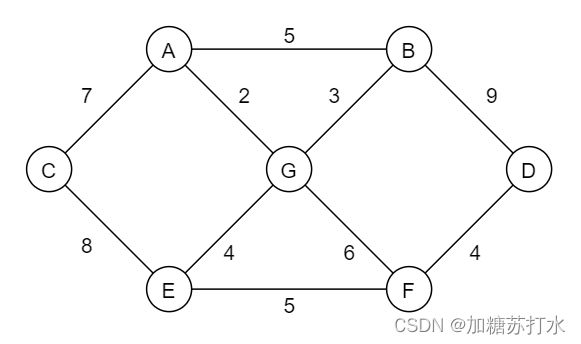
从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径，称为最短路径。如求下图从源点A出发到其他终点如D的最短距离。

1 Dijkstra算法简介

        迪克斯特拉算法使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题，算法最终得到一个最短路径树。该算法常用于路由算法或者作为其他图算法的一个子模块，且权值不能为负。//解释：广度优先的思想体现在每访问一个节点时，横向找到这个节点全部可以访问的其他节点。

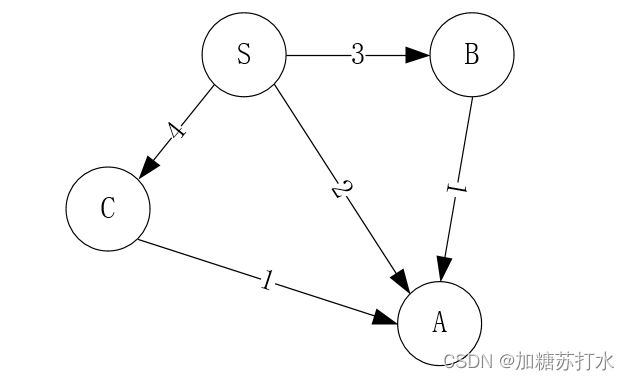
        Dijkstra算法采用的是一种贪心的策略。Dijkstra的核心定理是如果从源点直接到节点A的距离小于从起点直接到其他节点（如B、C）的距离，那么如果有从源点经其他节点的其他路径（如S-B-A，S-C-A）可以到达节点A，（即便B-A，C-A非常小）这些途径的总距离也会大于从源点到节点A的距离。

2 Dijkstra算法的思路

（1）前期准备：图的顶点数组 vertexes；各顶点的路径权重数组 matrix；

（2）首先声明一个数组 dis 来保存源点 s 到各个顶点的最短距离和一个保存各顶点是否已经被访问的数组 visited。初始时，源点 s 的路径权重被赋为 0 （dis[s] = 0）。若对于顶点 s 存在能直接到达的节点 m，则把 dis[m] 设为 matrix(s, m)，同时把所有其他（s不能直接到达的）顶点的路径长度设为无穷大。

（3）定义一个方法，返回当前 dis 数组中最小值的索引来判断下个要访问的节点，索引记为key，则该最小值就是源点 s 到该值对应的顶点的最短距离，返回前将该节点对应 visited 置为 true，表示已经访问完成（得到起点到该节点的最短路径被找到）。//解释：dist 数组的最小值代表现在源节点到各个节点的最短距离中最小的。该最小值此时已经可以确定为源点到这个节点的最短距离，因为后面哪怕还有其他未访问的节点，依据核心定理，他们的距离不可能比现在这个最小值还小了。

（4）在 visited 加入新的顶点后，如果这个节点可以到达其他顶点，检查源点经该顶点到达其他终点 j 的路径总长 len 是否比源点直接到达或之前记录的途径 dis[j] 短（源节点不能直接到达的节点距离设为无穷大，则必然小于这条新途径的距离），如果是，那么就更新这些可以到达的顶点在 dis 中的值。//解释：这个路径总长 len 可以拆解为从源点到中间节点的距离 dis[key]，加上中间节点到终点的距离 matrix[key][j]，这个总长不论中间节点有几个，总是可以这样表示。

（5）又从 dis 中找出最小值，重复上述动作，直到 visited 中包含了图的所有顶点。

ps: 可以增加一个 parent 数组来记录到达其他节点的前驱节点，即源点是经由哪个中间节点（或者就是从源点直接到该节点）到达该节点的，该步非必要，可以添加到（4）步中在更新时一起完成。

以上，除权重数组 matrix，其他数组均为一维数组。

3 代码实现

package algorithm.greedy_algorithm.dijkstra;
​
​
import java.util.Arrays;
​
/**
 * @Author Administrator
 * @Create 2023-09-02 19:42
 * @Version 1.0
 * ClassName DijkstraAlgorithm
 * Package algorithm.greedy_algorithm.dijkstra
 * Description
 */
public class DijkstraAlgorithm {
    public static void main (String[] args){
        //定义一个无穷大数来表示顶点之间没有连接
        final int INF = 10000;
        //顶点数组
        char[] vertexes = new char[]{'A','B','C','D','E','F','G'};
        //邻接矩阵
        int[][] matrix = new int[][]{
                {INF, 5, 7, INF, INF, INF, 2},
                {5, INF, INF, 9, INF, INF, 3},
                {7, INF, INF, INF, 8, INF, INF},
                {INF, 9, INF, INF, INF, 4, INF},
                {INF, INF, 8, INF, INF, 5, 4},
                {INF, INF, INF, 4, 5, INF, 6},
                {2, 3, INF, INF, 4, 6, INF}
        };
        Graph graph = new Graph(vertexes, matrix);
        int index = (int)(Math.random() * vertexes.length);//源节点可以自由选择
        System.out.println("选取的源节点是 "+index);
        dijkstra(graph,index);
​
    }
    //迪克斯特拉算法核心代码
    public static void dijkstra(Graph graph,int index){//index 是源点的下标
        int len = graph.matrix.length;
        final int INF = 10000;
​
        //源点 s 到各个顶点的最短距离
        int[] dis = new int[len];
        //记录顶点是否已经找到了最短路径
        boolean[] visited = new boolean[len];
        //记录节点的父节点
        int[] parent = new int[len];
​
        //先把到各点最短距离都初始化为无穷大
        //各点都初始化为没有父节点
        // 先把各点都初始化为未访问
        Arrays.fill(dis,INF);
        Arrays.fill(parent,-1);
        Arrays.fill(visited,false);
​
        //源点到自己的距离为0
        dis[index]=0;
​
​
        //更新源点到节点的距离//更新节点的父节点
        for(int i=0;i

---

复盘：

（1）迪克斯特拉算法与普利姆算法是相似的，都是每轮从一个记录到各个节点最短距离的数组中找到最小的节点来作为访问节点，在访问后更新到其他节点的距离。不同之处在于，普利姆算法是找到当前已访问的节点到其他节点的距离的最小值，而迪克斯特拉算法是从源节点到其他节点的距离的最小值，这个最小值可能是从源节点出发经过已访问节点再到终点的距离，需要作比较和叠加。

（2）迪克斯特拉算法的时间复杂度与普利姆算法一样，都是O(n2)，与节点个数相关。