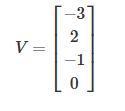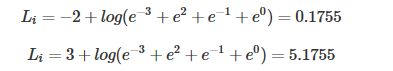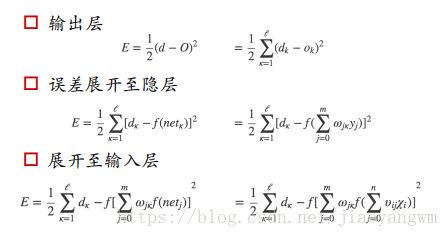【深度学习与计算机视觉】8、深度学习背景与人工神经网络
文章目录
-
- 一、基础知识
- 二、神经网络
-
- 2.1 神经网络的结构:
- 2.2 为什么神经网络在分类问题中的效果比较好:
- 2.3 BP算法
一、基础知识
线性分类器:
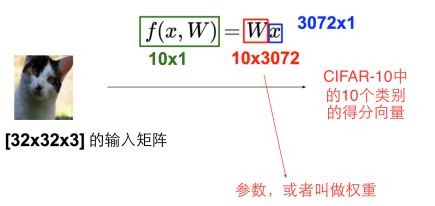
工业界有很多算法完成分类的问题,比如线性分类器,输入一张32x32x3的矩阵,利用f(wx+b)得到属于不同类别的得分向量,
方便演示,x列向量只选了4个值,w为3x4的矩阵,偏置项是为了让分类线可以上下平移,更好的分类,我们希望正确类别的得分比较高。

两种理解方式:
1. 空间划分
可以把w看成三个行向量,因为每个行都控制着不同类别的得分,三行w分别对应不同的直线。当我们确定了w和b之后,会确定一条直线,相当于对平面进行了一个划分。
不同的w和b对应空间中不同的超平面,对平面做区域划分,在不同区域内,属于不同的类。

2. 模板匹配
将每一行w看成每个类别的模板,
对同一个输入x,用不同的模板去匹配它,看哪个模板的匹配度最高。
损失函数:
损失函数是衡量预测和真实值的差别的,随机初始化一组w之后,会根据最小化损失函数的方法来优化w,使得损失函数最小。
不同的损失函数,对应不同的评估手段,不同的手段都能体现模型的学习能力,比如hingeloss,或softmax。
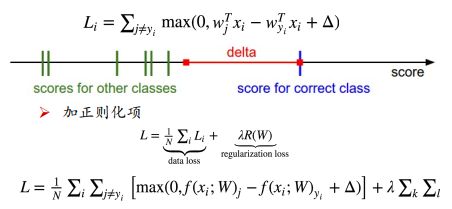
正确的得分比错误的得分大于delta的时候,不做惩罚,如果两者的差小于delta,则利用两者的差+delta作为损失值。
- 交叉熵损失
为什么可以用交叉熵损失函数来衡量网络?
熵的本质是信息量的期望值, H ( p ) = ∑ p i × H ( p i ) H(p)=\sum p_i\times H(p_i) H(p)=∑pi×H(pi),现在有关于样本集的两个分布p和q,其中p为真实分布,q为预测分布,比如深度学习的手写体识别,预测得到的属于每类的概率为 q ( 0 ) = 0.0 , q ( 1 ) = 0.1 , q ( 2 ) = 0.1 , q ( 3 ) = 0.8 , q ( 4 ) = 0 , … q(0)=0.0,q(1)=0.1,q(2)=0.1,q(3)=0.8,q(4)=0,… q(0)=0.0,q(1)=0.1,q(2)=0.1,q(3)=0.8,q(4)=0,…,q是真实的分布。最后肯定会选择概率最大的3作为输出,而真实分布为 p ( 0 ) = 0 , p ( 1 ) = 0 , p ( 2 ) = 0 , p ( 3 ) = 1 , p ( 4 ) = 0... p(0)=0,p(1)=0,p(2)=0,p(3)=1,p(4)=0... p(0)=0,p(1)=0,p(2)=0,p(3)=1,p(4)=0...,于是,我们想做的就是让p和q的分布尽可能一样。
概率论或信息论中,利用KL散度(相对熵)来衡量两个分布间的距离,且是非对称的,也就是 D ( P ∣ ∣ Q ) ≠ D ( Q ∣ ∣ P ) D(P||Q)\neq D(Q||P) D(P∣∣Q)=D(Q∣∣P),信息论中,也用 D ( P ∣ ∣ Q ) D(P||Q) D(P∣∣Q)来衡量利用概率分布Q来拟合真实分布P的时候,产生的信息损耗。当KL散度的值越大,表示两个概率分布的差距越大,KL散度和交叉熵的关系如下:
KL散度: D K L = ∑ p i l o g p i q i D_{KL}=\sum p_ilog \frac{p_i}{q_i} DKL=∑pilogqipi
交叉熵(CH):
C H ( p i , q i ) = − ∑ p i l o g q i = ∑ p i l o g p i − ∑ p i l o g q i − ∑ p i l o g p i CH(p_i,q_i)=-\sum p_i log q_i=\sum p_ilogp_i-\sum p_i log q_i-\sum p_ilogp_i CH(pi,qi)=−∑pilogqi=∑pilogpi−∑pilogqi−∑pilogpi ∴ C H ( p i , q i ) = H ( p i ) + ∑ p i l o g p i q i \therefore CH(p_i,q_i)=H(p_i)+\sum p_ilog \frac{p_i}{q_i} ∴CH(pi,qi)=H(pi)+∑pilogqipi
交叉熵=熵+KL散度
而 H ( p i ) H(pi) H(pi)是一个真实分布的期望,因此与训练无关,是一个常数项,所以将原本的最小化相对熵,转化为最小化交叉熵,
一般情况,我们希望将得分函数转化为分为某一类的概率,多分类情况下利用softmax来完成。
softmax:某个类别的得分的指数值,和所有得分的指数值的比值
为什么用指数,因为指数可以避免负值的出现。
S i = e V i ∑ j e V j S_i=\frac{e^{V_i}}{\sum_j e^{V_j}} Si=∑jeVjeVi
softmax可以将不同的得分函数转化为属于该类的概率值,转化之后,概率之和为1。
e V i e^{V_i} eVi表示某个类别的线性得分函数, S i S_i Si表示属于该类的概率输出,由于log变换不会影响函数的单调性,故对 S i S_i Si进行log变换,我们希望 S i S_i Si越大越好,即对应正确类别的相对概率越大越好,所以对 S i S_i Si前面加一个负号,来表示损失函数,这就称为交叉熵损失函数。
交叉熵损失函数: L i = − l o g ( e V i ∑ e V j ) L_i=-log(\frac{e^{V_i}}{\sum e^{V_j}}) Li=−log(∑eVjeVi)
对上式进行进一步处理,约掉指数:
L i = − l o g e V i − l o g ∑ j e V j = − V j + l o g ∑ j e V j L_i=-loge^{V_i}-log\sum_j e^{V_j}=-V_j+log\sum_j e^{V_j} Li=−logeVi−logj∑eVj=−Vj+logj∑eVj
损失函数越小越好
二、神经网络
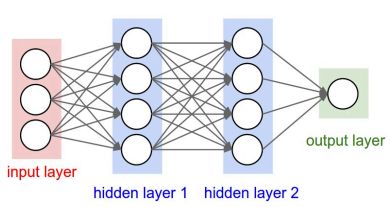
2.1 神经网络的结构:
由输入+隐层+输出来构成
从逻辑回归到神经元感知器:
已最简单的结构来剖析神经网络:感知器
线性输出:
z = θ 0 + θ 1 + θ 2 z=\theta_0+\theta_1+\theta_2 z=θ0+θ1+θ2
经过sigmoid映射到0~1的范围内的概率:
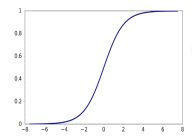
a = g ( z ) = 1 1 + e − z a=g(z)=\frac{1}{1+e^{-z}} a=g(z)=1+e−z1
利用阈值0.5作为判定是正类还是负类
添加少量的隐藏层:
2.2 为什么神经网络在分类问题中的效果比较好:
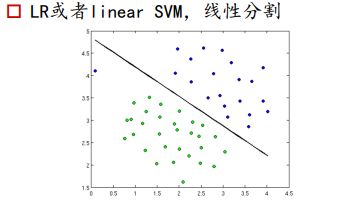
LR或SVM是线性分类器,是利用一条决策边界,去将正负样本区分开
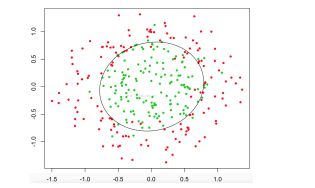
对于非线性可以的情况:
SVM会用核函数来升维,但是做不了可视化,无法看到升维之后的样本是什么样子的,维度很高,无法判断哪些特征有用,不可控性高。
如何用线性分类器做非线性分类——GBDT或kernel SVM,但是这些方法对划分的准确率却没有那么高。
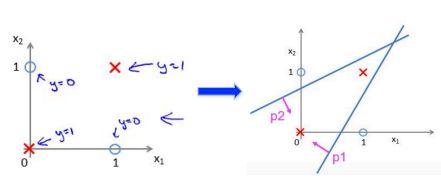
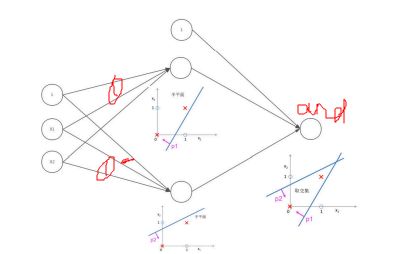
神经网络如果划分线性不可分的数据:
左图两类样本点的分割,线性分类器实现不了,右图是利用两条直线,将空间区分成了两部分,求两个直线的交集即可。
神经元完成逻辑与:
-
如果X1=0,X2=0,经过sigmoid之后,输出p->0;
-
如果X1=0,X2=1,那么-10经过sigmoid之后,p结果仍然接近于0
-
如果X1=1,X2=0,那么-10经过sigmoid之后,p结果仍然接近于0
-
如果X1=1,X2=1,那么10经过sigmoid之后,p结果接近于1
所以,感知器可以完成and的操作,当两个输入都为1的时候,输出才为1
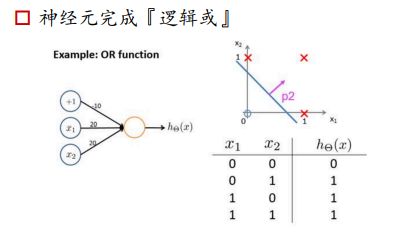
神经元完成逻辑或:
只要有1出现,那么输出都为1
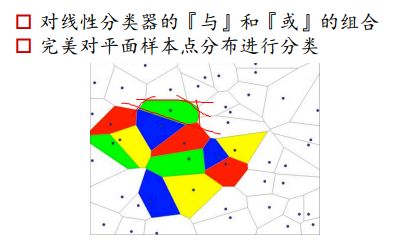
神经网络如何完成非线性的分类:
构建多个线性分类器,利用and操作来截出一个多边形区域。找到三个绿色的区域,对绿色区域进行一个or操作,就可以得到所有的绿色区域。
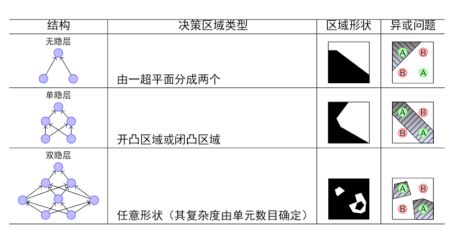
多加一个神经元,可以多一条线,多加一层,可以多加一个or操作,多层可以实现异或问题。
神经网络的结构:
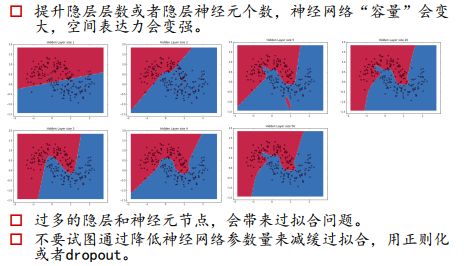
如果不添加非线性的激活函数的话,相当于线性变换的堆叠,还是没有逼近任何非线性信号的能力。
没有必要去深扣每个神经元到底在提取什么信号
2.3 BP算法
正向传播:求损失
反向传播:回传误差,根据误差信号修正每层的权重
前面的所有层都要对最后的预测负责,所以要将误差一层一层的往前传,更新每个神经元的参数。
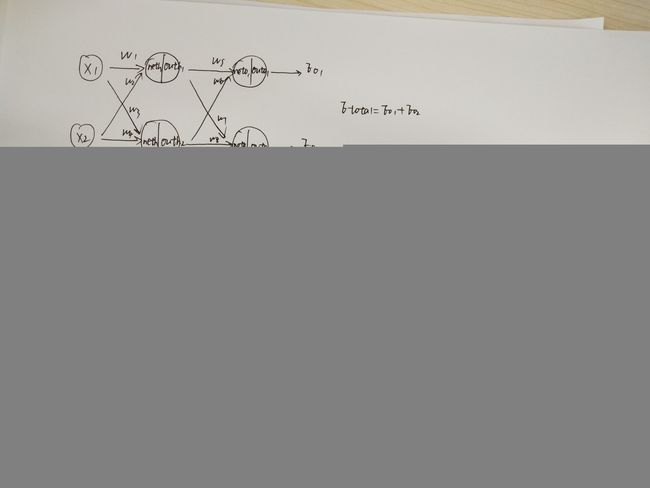
以3层感知器为例:
标准答案是[d1,d2,…,dL](回归利用L2损失)
求函数的最小值,一般用一阶的方式来求解,二阶的Hessian矩阵存储所需内存很大,难以实现。
SGD最小化误差函数:
复合函数 f ( g ( h ( x ) ) ) f(g(h(x))) f(g(h(x)))的导数,是链式法则,也就是 h ′ ( x ) ⋅ g ( h ( x ) ) ⋅ f ′ ( g ( h ( x ) ) ) h'(x)\cdot g(h(x))\cdot f'(g(h(x))) h′(x)⋅g(h(x))⋅f′(g(h(x))),需要一步步往前推导,得到f对x的偏导。
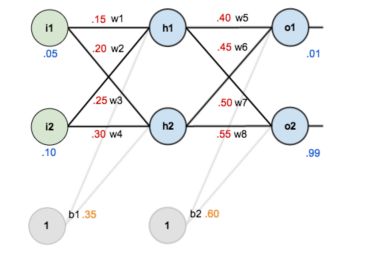
BP算法的示例:
希望找到合适的w和b,使得结果为0.01和0.99。
前向传播计算误差:
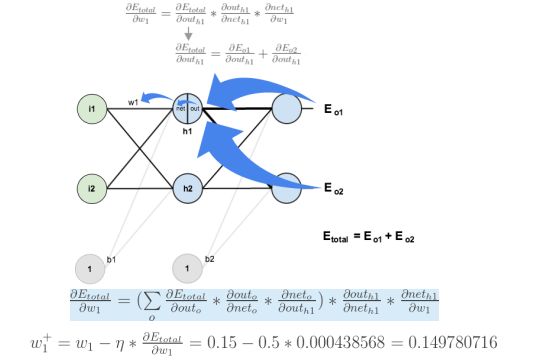
反向传播计算梯度:
w1对Etotal都会起作用,也就是Etotal=Etotal1+Etotal2,是一个求和的过程。
反向传播是将误差对该权值的梯度回传,利用该梯度进行权重的更新。