简单记录牛客top101算法题初级题(C语言实现)BM12 单链表的排序
1. BM12 单链表的排序
输入:[1,3,2,4,5]
返回值:{1,2,3,4,5}
1.1 自己的整体思路
- 开始的时候使用冒泡排序,但是冒泡排序的时间复杂度是O(n^2),空间复杂度是O(1),但是时间复杂度超了。归并排序的空间复杂度是O(n),时间复杂度是O(nlogn),这里也就是用了归并排序的思想。
- 一直从链表的中间分割链表(用到了链表中的快慢指针,快指针、慢指针同时走,快指针走到链表尾部,慢指针指向链表的中点位置),直到每个子链表只包含一个元素为止。
- 依次拼接分割后的链表(各个单节点元素的大小进行比较后),形成了一个新的链表,就完成了排序。
// 合并两个有序链表
struct ListNode* merge(struct ListNode* left, struct ListNode* right) {
struct ListNode dummy; //栈上存储 ,也可以动态创建,堆上存储
/*
//堆上存储
struct ListNode *newNode = (struct ListNode *)malloc(sizeof(struct ListNode)); //增加一个新的结点
newNode->next = NULL; //新结点指向NULL
struct ListNode *newNode1 = newNode; //定义一个指针指向该头结点
*/
struct ListNode* tail = &dummy;
while (left && right) {
if(left->val < right->val){
tail->next = left;
left = left->next;
} else {
tail->next = right;
right = right->next;
}
tail = tail->next;
}
tail->next = left ? left : right; //将归并排序过程中左侧链表和右侧链表合并成一个有序链表。如果left不为空,则返回left,否则返回right。因为链表长短,去掉公共的,长的就继续接上。
return dummy.next;
}
// 归并排序函数
struct ListNode* sortInList(struct ListNode* head) {
if (!head || !head->next) { //链表为空,或者链表只有一个元素
return head;
}
// 使用快慢指针找到链表的中点
struct ListNode* slow = head;
struct ListNode* fast = head;
while (fast->next && fast->next->next) {
slow = slow->next;
fast = fast->next->next;
}
struct ListNode* left = head; //头结点成为左结点
struct ListNode* right = slow->next; //慢指针(中间指针)的下一个指针赋值给右指针
slow->next = NULL; //断开链表指针,中间指针指向NULL
left = sortInList(left); //递归
right = sortInList(right); //递归
return merge(left, right); //拼接字符串
}
举例说明:
//以这个链表为例
4 -> 2 -> 1 -> 3 -> 5
1.sortInList 开始排序整个链表,分为左侧 left 和右侧 right。
left:4 -> 2 -> 1
right:3 -> 5
2.对 left 递归排序,分解为:
left_left:4
left_right:2 -> 1
3.继续对 left_right 递归排序,分解为:
left_right_left:2
left_right_right:1
4.合并 left_right_left 和 left_right_right,得到 left_right:1 -> 2
5.继续递归排序 left_left,得到 left_left:4
6.对 right 递归排序,分解为:
right_left:3
right_right:5
7.合并 left_left 和 left_right,得到 left:1 -> 2 -> 4
8.合并 right_left 和 right_right,得到 right:3 -> 5
9.最后,合并 left 和 right,得到最终的排序链表:1 -> 2 -> 3 -> 4 -> 5
1.2 其他的方法(大佬方法)
//使用快速排序
//快速排序中使用了双指针,对于链表,不是很好操作,这里把链表转成数组,把数组排好序后,再转成链表
int patition(int* arr, int low, int high){
int temp = arr[low]; //选择基准元素
while(low < high){
while(low < high && arr[high] >= temp){ //检测右边是否都大于基准元素
high--;
}
arr[low] = arr[high]; //把小于基准元素的值放到起始位置
while(low < high && arr[low] <= temp){
low ++;
}
arr[high] = arr[low]; //把大于基准元素的值放到又边位置
}
arr[low] = temp; //low = high时候,放上基准元素
return low; //返回索引,完成一次排序
}
void quickSort(int *a, int low, int high){
if(low < high){
int loc = patition(a, low, high); //loc是基准索引位置
quickSort(a, low, loc - 1); //递归基准索引前段
quickSort(a, loc + 1, high); //递归基准索引后段
}
}
struct ListNode* sortInList(struct ListNode* head ) {
if(head == NULL || head ->next == NULL){ //如果为空,或者只有一个元素,返回自身
return head;
}
int count = 0;
struct ListNode* p = (struct ListNode*)malloc(sizeof(struct ListNode)); //创建一个新指针
p = head; //指针指向头结点
while(p != NULL){ //计算链表的长度
count++;
p = p->next;
}
int* arr = (int*)malloc(sizeof(int)*count); //申请和链表长度一样的数组
p = head; //指针回到头指针
int i = 0;
while(p!=NULL){
arr[i] = p->val; //把链表的值赋值给数组
p = p->next;
i++;
}
quickSort(arr, 0, count - 1); //调用快速排序
p = head;
for(i = 0; i < count; i++){ //依次替换链表中的值,使得链表有序
p->val = arr[i];
p = p->next;
}
return head;
}
1.3 小结
1.3.1 各种简单常用排序方法
1.3.1.1 冒泡排序
简介:冒泡排序(Bubble Sort)是一种简单的排序算法,其基本思想是从列表的一端开始,依次比较相邻的两个元素,如果它们的顺序不正确就交换它们,然后继续向列表的另一端移动,重复这个过程,直到整个列表变得有序为止。
在最坏情况下,冒泡排序需要进行 n-1 轮比较和交换,其中 n 是待排序元素的数量。在每一轮中,需要比较相邻的元素并进行交换。所以,在最坏情况下,总的比较次数为 (n-1) + (n-2) + … + 1 = n * (n-1) / 2。因此,冒泡排序的时间复杂度为O(n^2)。
冒泡排序的空间复杂度主要取决于交换元素时所使用的临时变量。在每次交换过程中,只需要一个临时变量来存储一个元素的值,因此空间复杂度为O(1)。
举例说明:
#include 1.3.1.2 选择排序
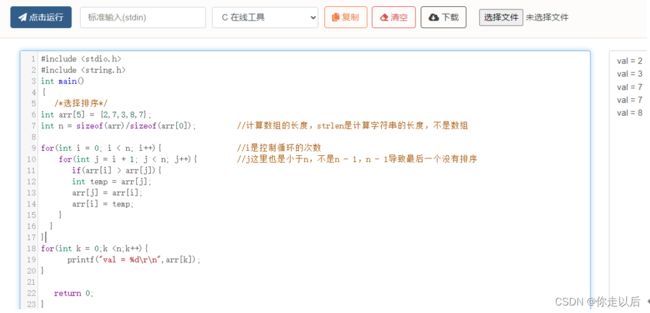
简介:选择排序(Selection Sort)是一种简单的排序算法,它的基本思想是在未排序的部分中找到最小(或最大)的元素,然后将其放到已排序部分的末尾。重复这个过程,直到整个数组都被排序。
时间复杂度:选择排序的时间复杂度是 O(n^2),其中 n 是元素的数量。
空间复杂度:选择排序的空间复杂度是 O(1),因为它仅需要一个常数级别的额外空间来存储临时变量。
#include 1.3.1.3 快速排序
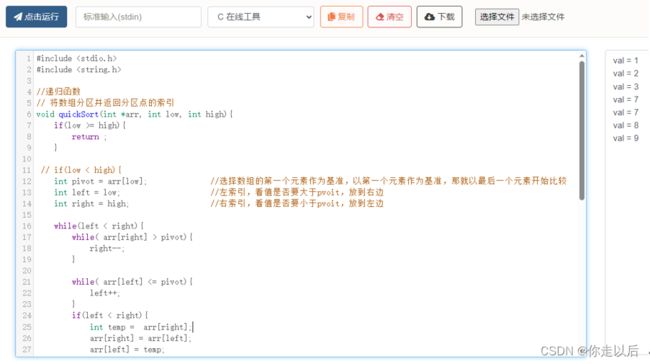
简介:快速排序(Quick Sort)是一种高效的、基于分治策略的排序算法。快速排序的核心思想是选择一个基准元素,将数组分成两个子数组,小于基准的元素放在左边,大于基准的元素放在右边,然后对这两个子数组分别进行递归排序。
快速排序的时间复杂度为O(nlog n),其中n是待排序元素的数量。
快速排序的空间复杂度为O(log n),其中n是待排序元素的数量。这是因为快速排序通常使用递归来进行分区,每次递归调用都会消耗一些栈空间。因此,递归的深度通常为O(log n)。这使得快速排序对于内存的消耗较低。
步骤:
- 选择基准元素: 从待排序的数组中选择一个元素作为基准元素。通常选择第一个元素、最后一个元素或中间元素作为基准。
- 分区(Partition): 将数组中的元素分成两部分,使得左边的元素都小于或等于基准元素,右边的元素都大于基准元素。分区过程可以使用多种方法,常见的是使用两个指针从数组的两端开始,向中间移动,交换不符合要求的元素,直到两个指针相遇。
- 递归排序: 递归地对分区后的两个子数组进行快速排序。分别对左边和右边的子数组重复上述两个步骤,直到子数组的大小为0或1,此时它们都被认为是有序的。
- 合并结果: 将排序后的子数组合并在一起,得到最终的有序数组。
举例说明:
#include 运行结果如下:
初始数组:2, 7, 3, 8, 7, 1, 9
1.quickSort(arr, 0, 6) - 调用 quickSort 函数,对整个数组进行排序。
2.第一次递归:
基准元素 pivot 选择为 2(第一个元素)。
左指针 left 初始化为 0,右指针 right 初始化为 6。
进入循环,right 向左移动,直到找到小于等于 pivot 的元素为止,即 arr[5](值为 1)。
left 向右移动,直到找到大于 pivot 的元素为止,即 arr[1](值为 7)。
交换 arr[1] 和 arr[5],现在数组变为 2, 1, 3, 8, 7, 7, 9。
左指针 left 和右指针 right 继续移动,直到left的索引是2,就是值为3的时候,right的索引是1,值是1的时候,停止循环。
将 pivot(值为 2)放在正确的位置,把right的位上值放到首位置,基准元素放到right上,数组变为 1, 2, 3, 8, 7, 7, 9。
对于 quickSort(arr, 0, 0),因为只有一个元素,递归结束,左侧子数组变为 1。
对于 quickSort(arr, 2, 6),继续进行递归。3,8,7,7,9。和上面循环一样,不在赘述。
1.3.1.4 归并排序
归并排序(Merge Sort)是一种常见的排序算法,它采用分而治之(Divide and Conquer)的策略来排序数组或列表元素。下面是归并排序的主要步骤:
分割(Divide):将原始数组或列表分成两个较小的子数组(或子列表),每个子数组包含原始数据的一半。这个步骤递归地继续,直到每个子数组只包含一个元素为止。
合并(Merge):将两个子数组或子列表合并为一个新的有序数组或列表。这是通过逐个比较两个子数组(或子列表)的元素并将其按顺序放入新的数组(或列表)中来完成的。这个过程一直持续到所有元素都被合并到一个有序数组(或列表)中。
递归:重复上述步骤,直到整个数组(或列表)已经被合并成一个有序序列。
在任何情况下,归并排序的时间复杂度都是O(nlog n)。在经典的归并排序实现中,通常需要O(n)的额外空间来存储临时数组,用于合并过程。此外,递归版本的归并排序还需要O(log n)的栈空间,因为递归调用栈的深度最多为log n层。一般认为归并排序的时间复杂度是O(n log n),而空间复杂度是O(n)。
举例说明:
#include 1.3.1.5 堆排序
堆排序(Heap Sort)是一种基于二叉堆数据结构的排序算法,它具有稳定的时间复杂度O(n log n),并且不需要额外的辅助存储空间。以下是堆排序的基本步骤:
建立最大堆(Build Max Heap):首先,将待排序的数组视为一个二叉堆(通常是一个数组的形式),并从最后一个非叶子节点开始,逐步将数组调整为最大堆。最大堆是一种二叉树,其中每个节点的值都大于或等于其子节点的值。
堆排序(Heapify):将最大堆的根节点(即数组的第一个元素)与堆的最后一个元素交换。然后,减小堆的大小并重新调整堆,以确保新的根节点是剩余元素中的最大值。重复这个过程,直到整个数组有序。
整个过程的思路是,从堆中不断选择最大的元素,将其放在数组的末尾,然后将剩余的元素重新构建为最大堆,重复这个过程直到整个数组都排好序。这就是堆排序的核心思想。
#include 
上述代码举例说明:
初始的数组是12, 11, 13, 5, 6, 7。
构建大根堆,堆中的每个节点的值都大于或等于其子节点的值。这意味着堆的根节点始终包含堆中的最大元素。
 第一次交换首位元素,并大根堆化:
第一次交换首位元素,并大根堆化:

第二次交换首位元素,并大根堆化:

第三次交换首位元素,并大根堆化:

第四次交换首位元素,并大根堆化,此时i = 2 ,left = 1,right = 2,不再与右边的值交换:

第五次交换首位元素,并大根堆化,此时i = 1 ,left = 1,right = 2,不再与左边和右边的值交换(也就是最后一次交换):
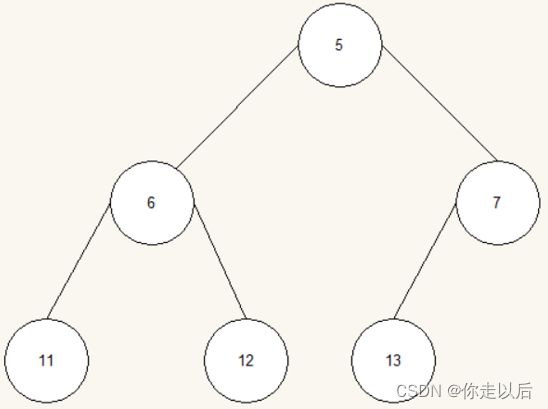
最后的排序结果就是:5, 6, 7, 11,12, 13。