uva 11178 - Morley's Theorem

 

http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2119

 

11178 - Morley's Theorem

Time limit: 3.000 seconds

Problem D
Morley’s Theorem
Input: Standard Input

Output: Standard Output

 Morley’s theorem states that that the lines trisecting the angles of an arbitrary plane triangle meet at the vertices of an equilateral triangle. For example in the figure below the tri-sectors of angles A, B and C has intersected and created an equilateral triangle DEF.

 

 

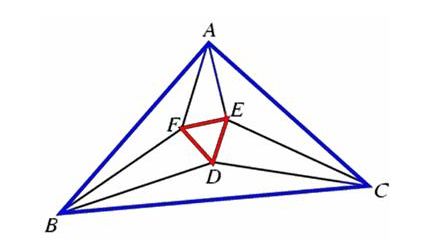
Of course the theorem has various generalizations, in particular if all of the tri-sectors are intersected one obtains four other equilateral triangles. But in the original theorem only tri-sectors nearest to BC are allowed to intersect to get point D, tri-sectors nearest to CA are allowed to intersect point E and tri-sectors nearest to AB are intersected to get point F. Trisector like BD and CE are not allowed to intersect. So ultimately we get only one equilateral triangle DEF. Now your task is to find the Cartesian coordinates of D, E and F given the coordinates of A, B, and C.

 

Input

First line of the input file contains an integer N (0<N<5001) which denotes the number of test cases to follow. Each of the next lines contain six integers xa , ya,xb , yb,xc , yc. This six integers actually indicates that the Cartesian coordinates of point A, B and C are  (xa , ya) , (xb , yb)and (xc , yc)respectively. You can assume that the area of triangle ABC is not equal to zero,  0 <= xa, ya , xb , xc , yb , yc <= 1000 and the points A, B and C are in counter clockwise order.

 

Output

For each line of input you should produce one line of output. This line contains six floating point numbers  xd , yd , xe , ye , xf , yf separated by a single space. These six floating-point actually means that the Cartesian coordinates of D, E and F are  (xd , yd) , (xe , ye) , (xf , yf)respectively. Errors less than   10 ^ -5will be accepted.

 

Sample Input   Output for Sample Input

2 1 1 2 2 1 2 0 0 100 0 50 50

1.316987 1.816987 1.183013 1.683013 1.366025 1.633975 56.698730 25.000000 43.301270 25.000000 50.000000 13.397460

 

 

 

 

Problemsetters: Shahriar Manzoor

Special Thanks: Joachim Wulff

 

分析：

STL

 

 

AC代码：

 

  1 // UVa11178 Morley's Theorem

  2 

  3 #include<cstdio>

  4 

  5 #include<cmath>

  6 

  7  

  8 

  9 struct Point {

 10 

 11   double x, y;

 12 

 13   Point(double x=0, double y=0):x(x),y(y) { }

 14 

 15 };

 16 

 17  

 18 

 19 typedef Point Vector;

 20 

 21  

 22 

 23 Vector operator + (const Vector& A, const Vector& B) { return Vector(A.x+B.x, A.y+B.y); }

 24 

 25 Vector operator - (const Point& A, const Point& B) { return Vector(A.x-B.x, A.y-B.y); }

 26 

 27 Vector operator * (const Vector& A, double p) { return Vector(A.x*p, A.y*p); }

 28 

 29 double Dot(const Vector& A, const Vector& B) { return A.x*B.x + A.y*B.y; }

 30 

 31 double Length(const Vector& A) { return sqrt(Dot(A, A)); }

 32 

 33 double Angle(const Vector& A, const Vector& B) { return acos(Dot(A, B) / Length(A) / Length(B)); }

 34 

 35 double Cross(const Vector& A, const Vector& B) { return A.x*B.y - A.y*B.x; }

 36 

 37  

 38 

 39 Point GetLineIntersection(const Point& P, const Point& v, const Point& Q, const Point& w) {

 40 

 41   Vector u = P-Q;

 42 

 43   double t = Cross(w, u) / Cross(v, w);

 44 

 45   return P+v*t;

 46 

 47 }

 48 

 49  

 50 

 51 Vector Rotate(const Vector& A, double rad) {

 52 

 53   return Vector(A.x*cos(rad)-A.y*sin(rad), A.x*sin(rad)+A.y*cos(rad));

 54 

 55 }

 56 

 57  

 58 

 59 Point read_point() {

 60 

 61   double x, y;

 62 

 63   scanf("%lf%lf", &x, &y);

 64 

 65   return Point(x,y);

 66 

 67 }

 68 

 69  

 70 

 71 Point getD(Point A, Point B, Point C) {

 72 

 73   Vector v1 = C-B;

 74 

 75   double a1 = Angle(A-B, v1);

 76 

 77   v1 = Rotate(v1, a1/3);

 78 

 79  

 80 

 81   Vector v2 = B-C;

 82 

 83   double a2 = Angle(A-C, v2);

 84 

 85   v2 = Rotate(v2, -a2/3);

 86 

 87  

 88 

 89   return GetLineIntersection(B, v1, C, v2);

 90 

 91 }

 92 

 93  

 94 

 95 int main() {

 96 

 97   int T;

 98 

 99   Point A, B, C, D, E, F;

100 

101   scanf("%d", &T);

102 

103   while(T--) {

104 

105     A = read_point();

106 

107     B = read_point();

108 

109     C = read_point();

110 

111     D = getD(A, B, C);

112 

113     E = getD(B, C, A);

114 

115     F = getD(C, A, B);

116 

117     printf("%.6lf %.6lf %.6lf %.6lf %.6lf %.6lf\n", D.x, D.y, E.x, E.y, F.x, F.y);

118 

119   }

120 

121   return 0;

122 

123 }

View Code