【数据结构】栈和队列的实现及应用

---

需要云服务器等云产品来学习Linux的同学可以移步/-->腾讯云<--/-->阿里云<--/-->华为云<--/官网，轻量型云服务器低至112元/年，新用户首次下单享超低折扣。

---

一、栈的概念

二、Stack.h

三、Stack.c

1、栈的初始化和销毁

2、栈的进栈、出栈

3、栈的判空、访问栈顶元素、栈内元素个数

四、队列的概念

五、Queue.h

六、Queue.c

1、队列的初始化和销毁

2、队列的入队、出队

3、队列的判空

4、访问队头、队尾数据、统计队列长度

七、力扣中栈和队列OJ题

1、有效的括号

2、用队列实现栈

3、用栈实现队列

4、设计循环队列

---

栈和队列是一种数据结构，只规定了性质，并没有规定实现方式。

本文以顺序结构实现栈，链表方式实现队列。

一、栈的概念

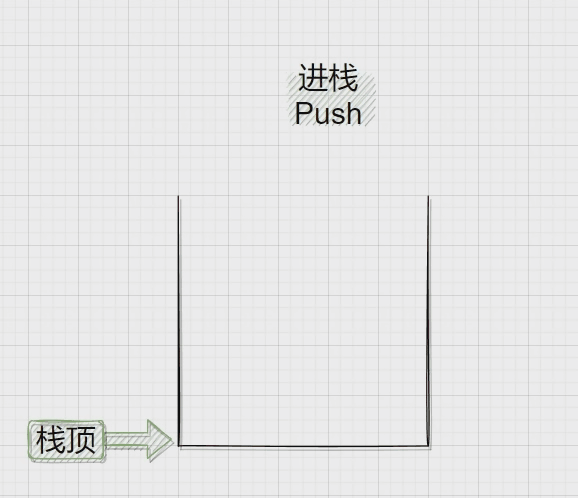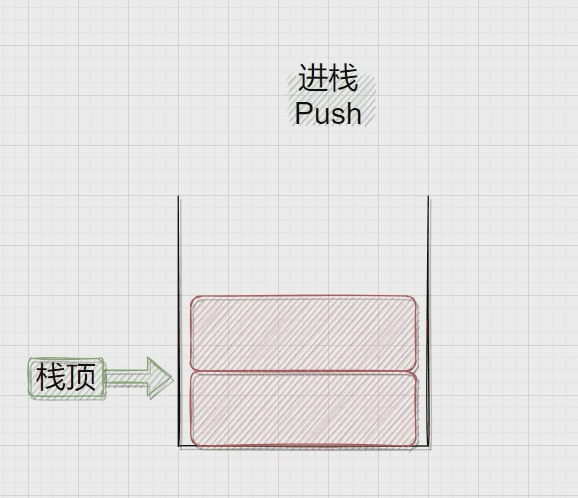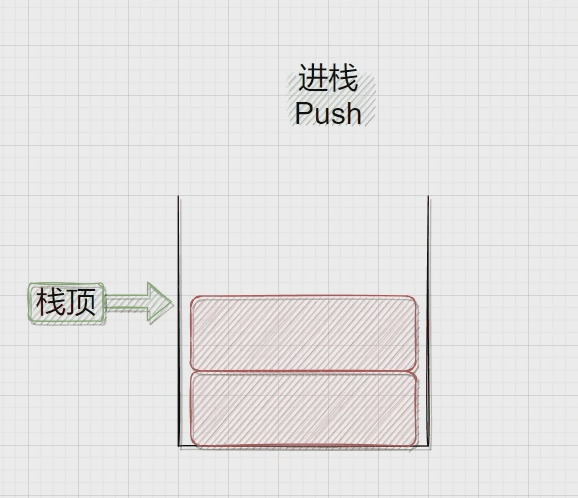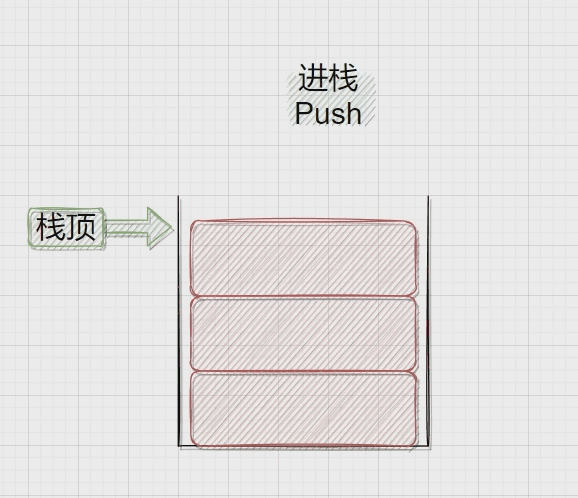
栈：是一种特殊的线性表，其只允许在栈顶进行插入和删除元素操作。

栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。

压栈：栈的插入操作叫做进栈\压栈\入栈，入数据在栈顶。

出栈：栈的删除操作叫做出栈。出数据也在栈顶。

二、Stack.h

#pragma once
#include 
#include 
#include 
#include 
typedef int STDataType;
typedef struct stack
{
	STDataType* arr;
	int top;//数组元素个数（top-1为最后一个元素的下标）就是顺序表的size
	int capacity;//总容量
}ST;
void StackInit(ST* ps);//初始化
void StackDestroy(ST* ps);//销毁
void StackPush(ST* ps, STDataType x);//压栈
void StackPop(ST* ps);//出栈
bool StackEmpty(ST* ps);//判断栈是不是为空
STDataType StackTop(ST* ps);//访问栈顶元素
int StackSize(ST* ps);//数组元素个数

以顺序结构实现栈，本质上仍是一个顺序表，只是这个顺序表加上了栈先进后出的规则。

数组的头是栈底，数组尾是栈顶。栈主要的压栈、出栈、访问栈顶等接口非常契合顺序表的尾插、尾删、随机访问的特点。

三、Stack.c

1、栈的初始化和销毁

void StackInit(ST* ps)//初始化
{
	assert(ps);
	ps->arr = NULL;
	ps->top = ps->capacity = 0;
}
void StackDestroy(ST* ps)//销毁
{
	assert(ps);
	free(ps->arr);
	ps->arr = NULL;
	ps->top = ps->capacity = 0;
}

和顺序表的初始化、销毁方式一样

2、栈的进栈、出栈

void StackPush(ST* ps, STDataType x)//进栈
{
	assert(ps);
	//判断扩容
	if (ps->top == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("realloc fail:\n");
			exit(-1);
		}
		ps->arr = tmp;
		ps->capacity = newCapacity;
	}
	ps->arr[ps->top] = x;
	ps->top++;
}
void StackPop(ST* ps)//出栈
{
	assert(ps);
	assert(!StackEmpty(ps));
	ps->top--;
}

进栈需要判断栈的空间，空间不够则需要扩容

出栈时，先判空，再将top--即可

3、栈的判空、访问栈顶元素、栈内元素个数

bool StackEmpty(ST* ps)//判断栈是不是为空
{
	assert(ps);
	return ps->top == 0;
}
STDataType StackTop(ST* ps)//访问栈顶元素
{
	assert(ps);
	assert(!StackEmpty(ps));
	return ps->arr[ps->top - 1];
}
int StackSize(ST* ps)//数组元素个数
{
	assert(ps);
	return ps->top;
}

注意访问栈顶元素这个接口，要先判断栈是不是空。

四、队列的概念

队列：一端进行插入数据操作，另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out)的特点。

入队列：进行插入操作的一端称为队尾

出队列：进行删除操作的一端称为队头

队列参照现实生活中的排队

五、Queue.h

#pragma once
#include 
#include 
#include 
#include 
typedef int QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;
typedef struct Queue
{
	QNode* head;
	QNode* tail;
	int size;//加个size，方便统计长度
}Queue;
void QueueInit(Queue* pq);//初始化
void QueueDestroy(Queue* pq);//销毁
void QueuePush(Queue* pq,QDataType x);//入队（尾插）
bool QueueEmpty(Queue* pq);//判断队列是否为空
void QueuePop(Queue* pq);//出队（头删）
int QueueSize(Queue* pq);//统计队列长度
QDataType QueueFront(Queue* pq);//访问队头数据
QDataType QueueBack(Queue* pq);//访问队尾数据

因为顺序结构不适合头删，这里使用单链表来实现队列。

结构体QNode用于模拟单链表，结构体Queue中存放了单链表的头、尾指针、链表节点个数。使用Queue来操纵单链表。

单链表的头head是队头（头删出数据），tail是队尾（尾插录数据）

六、Queue.c

1、队列的初始化和销毁

void QueueInit(Queue* pq)//初始化
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;
}
void QueueDestroy(Queue* pq)//销毁
{
	assert(pq);
	QNode* cur = pq->head;
    //逐个销毁释放空间
	while (cur)
	{
		QNode* del = cur;
		cur = cur->next;
		free(del);
	}
	pq->head = pq->tail = NULL;
}

和单链表的销毁方式一样，注意销毁时需要逐个节点销毁。

2、队列的入队、出队

void QueuePush(Queue* pq, QDataType x)//入队,尾插
{
	assert(pq);
    //创建一个新节点
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail:\n");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;
    //队列为空时的尾插和不为空的尾插
	if (QueueEmpty(pq))
		pq->head=pq->tail = newnode;
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
	pq->size++;
}
void QueuePop(Queue* pq)//出队（头删）
{
	assert(pq);
	assert(!QueueEmpty(pq));
	QNode* next = pq->head->next;
	free(pq->head);
	pq->head = next;
	pq->size--;
}

入队：尾插一个节点

出队：头删一个节点

3、队列的判空

bool QueueEmpty(Queue* pq)//判断队列是否为空
{
	assert(pq);
	return pq->head == NULL;
}

4、访问队头、队尾数据、统计队列长度

int QueueSize(Queue* pq)//统计队列长度
{
	assert(pq);
	return pq->size;
}
QDataType QueueFront(Queue* pq)//访问队头数据
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->head->data;
}
QDataType QueueBack(Queue* pq)//访问队尾数据
{
	assert(pq);
	assert(!QueueEmpty(pq));
	return pq->tail->data;
}

访问接口，注意先判空。

七、力扣中栈和队列OJ题

1、有效的括号

使用队列来解决，创建一个栈，碰到左括号将其进栈，碰到右括号则访问栈顶元素，不相符则为false，迭代比较相符则为true

bool isValid(char * s){
    ST st;
    StackInit(&st);
    while(*s)
    {
        if(*s=='('||*s=='{'||*s=='[')
        {
            StackPush(&st,*s);//压栈
        }
        else//比较时的情况
        {
            if(StackEmpty(&st))
                return false;  
            else if(StackTop(&st)=='('&&*s!=')')//访问栈顶元素
            {
                return false;
            }
            else if(StackTop(&st)=='{'&&*s!='}')
            {
                return false;
            }
            else if(StackTop(&st)=='['&&*s!=']')
            {
                return false;
            }
            StackPop(&st);
        }
        ++s;
    }
    if(!StackEmpty(&st))
        return false;
    StackDestroy(&st);
    return true;
}

注：上述代码还需要将栈的实现的代码拷贝一份上去。

2、用队列实现栈

入栈：选择非空队列进行入栈

出栈：队列中只留一个元素，将其他元素Pop至另一个队列，再对那个遗留的元素执行出队列操作即可模拟出栈动作

typedef struct {
    Queue q1;
    Queue q2;
} MyStack;
MyStack* myStackCreate() {
    MyStack* obj=(MyStack*)malloc(sizeof(MyStack));
    QueueInit(&obj->q1);
    QueueInit(&obj->q2);
    return obj;
}

void myStackPush(MyStack* obj, int x) {
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);//入队,尾插
    }
    else
    {
        QueuePush(&obj->q2,x);//入队,尾插
    }
}

int myStackPop(MyStack* obj) {
    Queue* empty=&obj->q1;
    Queue* unEmpty=&obj->q2;
    if(QueueEmpty(&obj->q2))
    {
        empty=&obj->q2;
        unEmpty=&obj->q1;
    }
    while(QueueSize(unEmpty)>1)//将非空元素导入到空队列，留下最后一个
    {
        QueuePush(empty,QueueFront(unEmpty));//入队,尾插
        QueuePop(unEmpty);//出队（头删）
    }
    int top=QueueFront(unEmpty);
    QueuePop(unEmpty);//出队（头删）
    return top;
}

int myStackTop(MyStack* obj) {
    if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);//访问队尾数据
    }
    else
    {
        return QueueBack(&obj->q2);//访问队尾数据
    }
}

bool myStackEmpty(MyStack* obj) {
    return QueueEmpty(&obj->q1)&&QueueEmpty(&obj->q2);
}

void myStackFree(MyStack* obj) {
    QueueDestroy(&obj->q1);//销毁
    QueueDestroy(&obj->q2);//销毁
    free(obj);
}

注：上述代码还需要将队列的实现的代码拷贝一份上去。

3、用栈实现队列

现在有两个栈，第一个栈用于入栈、出栈至第二个栈的操作，第二个栈仅用于出栈操作。

入栈：在第一个栈中压入数据

出栈：如果第二个栈为空，则第一个栈中 数据全部出栈至第二个栈，由第二个栈专门执行出栈操作。等第二个栈再次为空，再次执行上述动作

MyQueue* myQueueCreate() {
    MyQueue* obj=(MyQueue*)malloc(sizeof(MyQueue));
    StackInit(&obj->st1);
    StackInit(&obj->st2);
    return obj;
}

void myQueuePush(MyQueue* obj, int x) {
    StackPush(&obj->st1, x);//压栈
}

int myQueuePop(MyQueue* obj) {
    if(StackEmpty(&obj->st2))
    {
        while(!StackEmpty(&obj->st1))
        {
            StackPush(&obj->st2, StackTop(&obj->st1));//压栈
            StackPop(&obj->st1);
        }
    }
    int val=StackTop(&obj->st2);
    StackPop(&obj->st2);
    return val;
}

int myQueuePeek(MyQueue* obj) {
    if(StackEmpty(&obj->st2))
    {
        while(!StackEmpty(&obj->st1))
        {
            StackPush(&obj->st2, StackTop(&obj->st1));//压栈
            StackPop(&obj->st1);
        }
    }
    return StackTop(&obj->st2);
}

bool myQueueEmpty(MyQueue* obj) {
    return StackEmpty(&obj->st1)&&StackEmpty(&obj->st2);
}

void myQueueFree(MyQueue* obj) {
    StackDestroy(&obj->st1);
    StackDestroy(&obj->st2);
    free(obj);
}

注：上述代码还需要将栈的实现的代码拷贝一份上去。

4、设计循环队列

typedef struct {
    int* arr;
    int front;//记录首
    int tail;//记录尾的下一个
    int capacity;//用于处理边界问题的一个变量
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->arr=(int*)malloc(sizeof(int)*(k+1));
    obj->front=obj->tail=0;
    obj->capacity=k+1;//这里一定要写成k+1，写成k的话,后续处理边界问题要额外考虑分支情况
    return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front==obj->tail;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->tail+1)%(obj->capacity)==obj->front;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
        return false;
    obj->arr[obj->tail]=value;
    obj->tail++;
    obj->tail%=obj->capacity;
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return false;
    obj->front++;
    obj->front%=obj->capacity;
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    return obj->arr[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    return obj->arr[(obj->tail-1+obj->capacity)%obj->capacity];
}
void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->arr);
    obj->arr=NULL;
    free(obj);
}

因为循环队列无法区分队列为空和为满的情况，因为为空和未满，首位下标是一样的。

所以这道题有两种解法，计数确定栈空栈满，或者多开辟一个空间。本题采用后者。

可选的数据结构也有两种，顺序和链表。本题采用顺序。

上表为队列满的情况，无法再执行插入。运用顺序表，本题的难点在于如何处理tail和front在数组尾部的情况。

强烈建议在初始化的接口中将capacity定义为k+1，因为入队出队接口中%capacity后，可以同时满足正常和极端位置下的情况。（详见代码，一读就懂，后续读者可以逝一下将capacity定义为k，感受下区别）

capacity定义为k时的代码如下：

typedef struct {
    int* arr;
    int front;//记录首
    int tail;//记录尾的下一个
    int capacity;//总容量
} MyCircularQueue;


MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue* obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    obj->arr=(int*)malloc(sizeof(int)*(k+1));
    obj->front=obj->tail=0;
    obj->capacity=k;
    return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    return obj->front==obj->tail;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    return (obj->tail+1)%(obj->capacity+1)==obj->front;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    if(myCircularQueueIsFull(obj))
        return false;
    obj->arr[obj->tail]=value;
    obj->tail++;
    if(obj->tail>obj->capacity)
        obj->tail=obj->tail%obj->capacity-1;
    return true;
}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return false;
    obj->front++;
    if(obj->front>obj->capacity)
        obj->front=obj->front%obj->capacity-1;
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    return obj->arr[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    if(obj->tail!=0)
        return obj->arr[(obj->tail-1+obj->capacity)%obj->capacity];
    return obj->arr[obj->capacity];
}
void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->arr);
    obj->arr=NULL;
    free(obj);
}

主要区别就是入队出队代码，常规情况和边界情况不能统一。