算法--岛屿问题(DFS/BFS/UF)
与岛屿有关的问题
岛屿问题属于图的搜索问题,一般使用DFS,BFS或者UF来解决。
判断搜索起始点,从某一点开始 或者要从所有点开始尝试所有可能;
对于每个点 向四周搜索 上下左右;
1.岛屿数量
https://leetcode-cn.com/problems/number-of-islands/
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
将二维数组每个元素看成顶点,将元素1与周边1相连,则二维数组转换为一幅图,即求解图连通分量的数量。
依次遍历顶点为1的点,利用DFS或者BFS来向四周搜索,如果相连搜索到1则将1置为0,最终DFS或者BFS搜索的次数就是岛屿的数量。
DFS
private static int[] dx = new int[]{1, -1, 0, 0};
private static int[] dy = new int[]{0, 0, -1, 1};
/**
* 给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
* 岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
* 此外,你可以假设该网格的四条边均被水包围。
* */
public int numIslands(char[][] grid) {
// 从顶点为1的点开始DFS 在遍历过程中访问的点变为0
// 最终DFS访问次数就是岛屿数量
if (grid == null || grid.length == 0) {
return 0;
}
int result = 0;
int rows = grid.length;
int cols = grid[0].length;
// 从每个顶点为1的点开始DFS
for (int i=0; i=rows || j<0 || j>=cols || grid[i][j] == '0') {
return;
}
// 当前位置置为0
grid[i][j] = '0';
// 向上下左右四个方向继续DFS
for (int k=0; k<4; k++) {
dfs(grid, i+dx[k], j+dy[k], rows, cols);
}
} BFS搜索
private static int[] dx = new int[]{1, -1, 0, 0};
private static int[] dy = new int[]{0, 0, -1, 1};
// BFS解法
public int numIslands2(char[][] grid) {
// 从每个顶点为1的点开始BFS 遍历过程中的点置为0 最终BFS的次数就是岛屿数量
if (grid == null || grid.length == 0) {
return 0;
}
int rows = grid.length;
int cols = grid[0].length;
int result = 0;
for (int i=0; i=rows || j<0 || j>=cols || grid[i][j]=='0') return;
Queue queue = new LinkedList<>();
grid[i][j] = '0';
queue.add(new int[]{i, j});
while (!queue.isEmpty()) {
int[] index = queue.poll();
int x = index[0];
int y = index[1];
for (int k=0; k<4; k++) {
int nx = x+dx[k];
int ny = y+dy[k];
if (nx<0 || nx>=rows || ny<0 || ny>=cols) continue;
if (grid[nx][ny] == '1') {
grid[nx][ny] = '0';
queue.add(new int[]{nx, ny});
}
}
}
} 2.岛屿的最大面积
https://leetcode-cn.com/problems/max-area-of-island/
给定一个包含了一些 0 和 1 的非空二维数组 grid 。
一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 0 。
岛屿数量是求解图的连通分量的个数,本题是求解最大连通分量,利用DFS来搜索,每搜索一次DFS返回本次搜索点的个数,最后返回所有搜索次数的最大值。
private static int[] dx = new int[]{1, -1, 0, 0};
private static int[] dy = new int[]{0, 0, -1, 1};
/**
* 给定一个包含了一些 0 和 1 的非空二维数组 grid 。
*
* 一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合,
* 这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。
* 你可以假设 grid 的四个边缘都被 0(代表水)包围着。
*
* 找到给定的二维数组中最大的岛屿面积。(如果没有岛屿,则返回面积为 0 。)
* */
public int maxAreaOfIsland(int[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
int rows = grid.length;
int cols = grid[0].length;
int maxArea = 0;
// 从每个顶点为1的点开始DFS
for (int i=0; i=rows || j<0 || j>=cols || grid[i][j] == 0) {
return 0;
}
// 当前位置置为0
grid[i][j] = 0;
int area = 1;
// 向上下左右四个方向继续DFS
for (int k=0; k<4; k++) {
area += dfsMaxArea(grid, i+dx[k], j+dy[k], rows, cols);
}
return area;
} 3.岛屿周长
https://leetcode-cn.com/problems/island-perimeter/
给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
网格中的格子 水平和垂直 方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
由题目可知 图中有且只有一个岛屿,观察岛屿周长的分部,当某个点为1 并且四周是0的边 并且四周不是1的边即为岛屿周长。
之前在遍历过程中会将访问的顶点1变为0 避免重复访问,这里为了避免统计周长重复 将访问过的1置为2 只统计访问过程中顶点1的四周是0的边数 如果是2 说明是岛屿内部 不是周长 直接跳过。
/**
* 给定一个 row x col 的二维网格地图 grid ,其中:grid[i][j] = 1 表示陆地, grid[i][j] = 0 表示水域。
* 网格中的格子 水平和垂直 方向相连(对角线方向不相连)。
* 整个网格被水完全包围,但其中恰好有一个岛屿(或者说,一个或多个表示陆地的格子相连组成的岛屿)。
* 岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。
* 格子是边长为 1 的正方形。网格为长方形,且宽度和高度均不超过 100 。计算这个岛屿的周长。
* */
public int islandPerimeter(int[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
int rows = grid.length;
int cols = grid[0].length;
int perimeter = 0;
// 从每个顶点为1的点开始DFS
// 在搜索过程中 对于搜索到的1 观察其四周非1的个数 即为边数
// 只有为1的点四周才会出现周长 因此遍历过程中对于每一个1的点都需要观察其四周是否是周长
// 当某个顶点1访问之后 不能标记为0 这样会与海洋0重复 这里标记为2
for (int i=0; i=rows || j<0 || j>=cols || grid[i][j] == 0) {
return 1;
}
if (grid[i][j] == 2) {
return 0;
}
// 当前位置置为0
grid[i][j] = 2;
int area = 0;
// 向上下左右四个方向继续DFS
for (int k=0; k<4; k++) {
area += dfsPerimeter(grid, i+dx[k], j+dy[k], rows, cols);
}
return area;
} 4.封闭岛屿数量
https://leetcode-cn.com/problems/number-of-closed-islands/
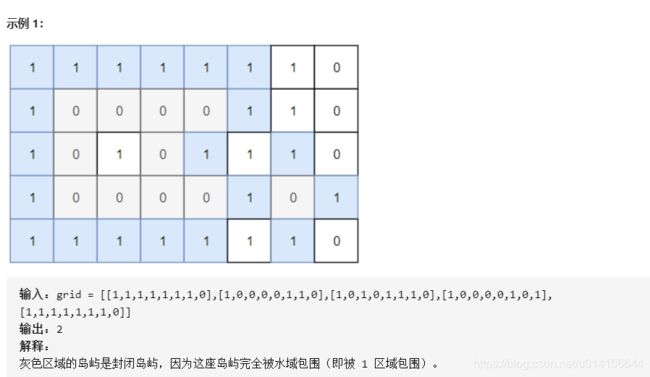
有一个二维矩阵 grid ,每个位置要么是陆地(记号为 0 )要么是水域(记号为 1 )。
我们从一块陆地出发,每次可以往上下左右 4 个方向相邻区域走,能走到的所有陆地区域,我们将其称为一座「岛屿」。
如果一座岛屿 完全 由水域包围,即陆地边缘上下左右所有相邻区域都是水域,那么我们将其称为 「封闭岛屿」。
请返回封闭岛屿的数目。
从i=1 j=1开始DFS搜索 到i=rows-1 j=cols-1结束
对于每一个0开始DFS 其可能会出现一个封闭岛屿 其条件是DFS搜索过程中四周全为1 或者说搜索到的0都不在边界上。
private static int[] dx = new int[]{1, -1, 0, 0};
private static int[] dy = new int[]{0, 0, -1, 1};
private int var = 0;
/**
* 有一个二维矩阵 grid ,每个位置要么是陆地(记号为 0 )要么是水域(记号为 1 )。
* 我们从一块陆地出发,每次可以往上下左右 4 个方向相邻区域走,能走到的所有陆地区域,我们将其称为一座「岛屿」。
* 如果一座岛屿 完全 由水域包围,即陆地边缘上下左右所有相邻区域都是水域,那么我们将其称为 「封闭岛屿」。
* 请返回封闭岛屿的数目。
* */
public int closedIsland(int[][] grid) {
if (grid == null || grid.length < 3 || grid[0].length < 3) {
return 0;
}
int rows = grid.length;
int cols = grid[0].length;
int result = 0;
for (int i=1; i=rows || j<0 || j>=cols) {
var = 0;
return;
}
// 如果当前位置为1 直接返回 继续DFS
if (grid[i][j] == 1) {
return;
}
grid[i][j] = 1;
// 向上下左右四个方向继续DFS
for (int k=0; k<4; k++) {
dfsClosedIsland(grid, i+dx[k], j+dy[k], rows, cols);
}
} 4.不同岛屿的数量
https://leetcode-cn.com/problems/number-of-distinct-islands/
5.岛屿数量II
https://leetcode-cn.com/problems/number-of-islands-ii/
6.被围绕的区域
https://leetcode-cn.com/problems/surrounded-regions/