2023.4.22PTA树1
文章目录
- 一,PTA树1
-
- 1.题目
- 2.
- 3.
一,PTA树1
1.题目
作者 严冰
单位 浙大城市学院
对以下算法功能最准确的描述是()。
int fun1(BTreeNode *BT, ElemType e){
int n1, n2;
if (BT==NULL) return 0;
if (BT->data==e) return 1;
n1 = fun1(BT->left, e);
if (n1>=1) return n1+1;
n2 = fun1(BT->right, e);
if (n2>=1) return n2+1;
return 0;
}
A.
判断二叉树根结点值是否为e
B.
判断二叉树是否存在值为e结点
C.
求二叉树中值为e结点的层次
D.
求二叉树值为e的结点的个数
选C,查找到值为e的结点就返回并从底层到上层每层递增1。
2.
分数 1
作者 严蔚敏
单位 清华大学
二叉树的形态
由 3 个结点可以构造出 ▁▁▁▁▁ 种不同形态的二叉树。
A.
2
B.
3
C.
4
D.
5
选d,可推出5种。
3.
分数 2
作者 王俊玲
单位 集美大学
一棵度为4的树T中,若有20个度为4的结点,10个度为3的结点,1个度为2的结点,10个度为1的结点,则树T的叶子结点个数是( )。
A.
41
B.
82
C.
113
D.
122
选b,由公式204+103+2+10+1-41=82.
##4.
分数 1
作者 张泳
单位 浙大城市学院
一棵二叉树中有7个叶子节点和5个单分支节点,其总共有( )个节点
A.
16
B.
18
C.
12
D.
31
选b,二叉树中每个双分支结点都会增加一个叶子结点,一共7个叶子结点即有6个双分支结点。
分数 1
作者 张泳
单位 浙大城市学院
深度为5的二叉树至多有 ( )个节点
A.
16
B.
32
C.
31
D.
10
选c,满二叉树一共2n-1个结点。
分数 1
作者 张泳
单位 浙大城市学院
一棵完全二叉树中有501个叶子节点,则至少有 ( ) 个节点
A.
501
B.
502
C.
1001
D.
1002
选c,已知n0=501,则n0=n2+1,得n2=500,因为完全二叉树里至多有1个n1结点,而题目里问至少有几个结点,则不需要n1,答案为1001个。
一棵高度为8的完全二叉树至少有( )叶子节点
A.
63
B.
64
C.
127
D.
128
选b,8层二叉树叶子结点最少时,第八层只有一个结点,实际双分支结点有27-1个,即叶子节点个数为27个。
一棵满二叉树中127个节点,其中叶子节点的个数是( )
A.
63
B.
64
C.
65
D.
不确定
选b,满二叉树中127个节点,既有26-1个双分支结点,所以就有26个叶子结点。
若一棵二叉树具有10个度为2的结点,5个度为1的结点,则度为0的结点个数是( )
A.
9
B.
11
C.
15
D.
不确定
选,度为0即为叶子结点,即为度为2结点数加1,为11.
Which one of the following statement is FALSE about a tree?
A.
When converting a tree into a binary tree using FirstChild-NextSibling representation, the root of the binary tree must be of degree 1.
B.
Every node in a nonempty tree is the root of some subtree.
C.
The degree of a tree is equal to the depth of the tree.
D.
Sibling nodes share the same parent.
翻译题,选b
A binary tree with 1325 nodes must have a height ____. (Assume the height of a single node tree is 0.)
A.
in the range [10, 1324]
B.
in the range [9, 1324]
C.
in the range [10, 1325]
D.
in the range [11, 662]
翻译题,选a。
若三叉树 T 中有 244 个结点(叶结点的高度为 1 ), 则 T 的高度至少是
A.
8
B.
7
C.
6
D.
5
选c,三叉数不过是把公式中底数改成3了,变成3n.
含n个结点的3次树的最小高度是( ),最大高度是( )。
A.
log3(2n-1),n-2
B.
log3(2n+1),n-1
C.
log3(2n-1),n-1
D.
log3(2n+1),n-2
选d,把n=4套入
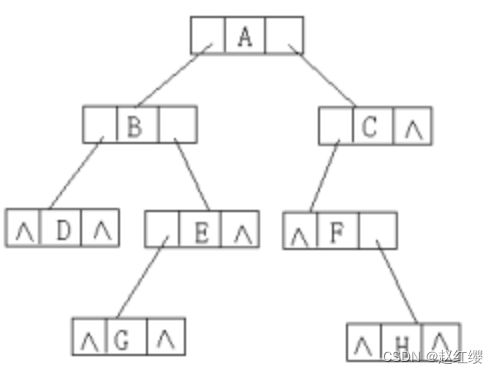
对于图所示二叉树,试给出:
QQ20190414-123721@2x.png
它的顺序存储结构
A.
ABCDEF^^^G^^H
B.
ABD^^EG^^^CF^H
C.
DBGE^A^FHC
D.
DGE^B^HFC^A
把一棵树转换为二叉树后,这棵二叉树的形态是( )。
A.
唯一的
B.
有多种
C.
有多种,但根结点都没有左孩子
D.
有多种,但根结点都没有右孩子
选a,操作肯定是唯一的,要不然怎么还原
利用二叉链表存储树,则根结点的右指针是( )。
A.
指向最左孩子
B.
指向最右孩子
C.
空
D.
非空
选c,以二叉链表作树的存储结构,即用孩子兄弟表示法来表示树,链表中结点的两个链域分别指向该结点的第一个孩子结点和下一个兄弟结点,根结点没有兄弟结点,所以右指针是空的
在下列存储形式中,( )不是树的存储形式。
A.
双亲表示法
B.
孩子链表表示法
C.
孩子兄弟表示法
D.
顺序存储表示法
选d,顺序存储只能用于二叉树,要不然无法对应双亲和兄弟结点。
Given a tree of degree 3. Suppose that there are 8 leaf nodes and 2 nodes of degree 3. Then the number of degree 2 nodes must be ____.
A.
0
B.
1
C.
2
D.
3
选d。
一棵高度为h的并且只有h个结点的二叉树,采用顺序存储结构存放在R[1…n]中,则n应该至多是( )。
A.
2h
B.
2h-1
C.
2h
D.
2h-1
选d,这个是网上查的,真不太会。
关于二叉树的存储结构,以下说法正确的是( )
A.
二叉树只有顺序存储结构
B.
二叉树只有链式存储结构
C.
二叉树既有顺序存储结构,又有链式存储结构
D.
二叉树的链式存储结构中只有一个指针域
根据定义,明显选C
一个深度为k的,具有最少结点数的完全二叉树按层次(同层次从左到右)用自然数依此对结点编号,则编号最大的非叶子的序号是( )。
A.
2^(k-2)
B.
2^(k-2)+1
C.
2^(k-1)+1
D.
2^(k-1)
编号最小的叶子结点序号是:2k-2+1 ,结点i所在的层次号为 [log2i]+1
用二叉链表表示具有n个结点的二叉树时,值为空的指针域的个数为( )
A.
n-1
B.
n
C.
n+l
D.
2n
选C
由n=n0+n1+n2,n0=n2+1,得n=n1+2n2+1;
因为二叉树,所以n1为0或1;
1)当n1为0时,n2=(n-1)/2,空指针:2n-2*(n-1)/2=n+1;
2) 当n1为1时,n2=(n-2)/2,空指针:2n-2*(n-2)/2-1=n+1.
某森林 F 对应的二叉树为 T,若 T 的先序遍历序列是 a, b, d, c, e, g, f,中序遍历序列是 b, d, a, e, g, c, f,则 F 中的树的棵树是:
A.
1
B.
2
C.
3
D.
4
选c。
给二叉树的结点编号
对一棵二叉树的结点从 1 开始顺序编号。要求每个结点的编号小于其左、右孩子的编号,且左孩子的编号小于右孩子的编号。可采用 ▁▁▁▁▁ 实现编号。
A.
先序遍历
B.
后序遍历
C.
中序遍历
D.
层次遍历
选c,不可采用层次遍历的原因是层次遍历顺序不一样 ,不遵守先左孩子后右孩子。
有关二叉树下列说法正确的是( )
A.
二叉树的度为2
B.
一棵二叉树的度可以小于2
C.
二叉树中至少有一个结点的度为2
D.
二叉树中任何一个结点的度都为2
明显选c。