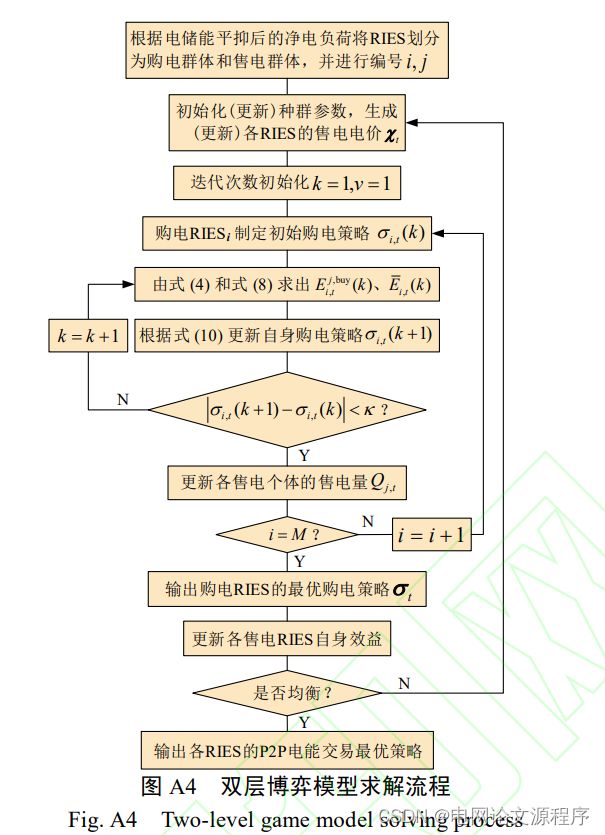
文章解读与仿真程序复现思路——电力自动化设备EI\CSCD\北大核心《氢耦合区域综合能源系统集群双层博弈随机优化调度策略》
这个标题涉及到复杂的领域,主要包括氢能源、能源系统集群、双层博弈、随机优化和调度策略。我将分步解读这个标题:
-
氢耦合区域综合能源系统集群:
- 氢能源: 这指的是使用氢作为能源的系统,可能是指氢燃料电池等。
- 区域综合能源系统集群: 这可能是指在特定地区集成和协调多种能源系统,包括但不限于电力、热能、氢能等,形成一个综合的能源系统网络。
-
双层博弈:
- 双层: 这可能指的是有两个层次或者水平的决策或竞争实体。
- 博弈: 这表示涉及决策者之间相互影响、相互竞争的情境,通常用于描述策略性的决策过程。
-
随机优化:
- 随机: 表示存在随机性或不确定性。
- 优化: 指的是通过调整参数或者变量,以使某个系统或过程达到最佳状态。
-
调度策略:
- 调度: 是指在一定的规则或策略下,安排和分配资源,使得系统能够有效地运行。
- 策略: 涉及选择和制定合适的行动计划,以达到特定的目标。
综合起来看,这个标题似乎描述了一个关于氢能源系统在某个区域中,通过综合能源系统集群的方式进行优化调度的问题,其中涉及到多层次的决策者(双层博弈),而优化过程中存在一定的随机性。这可能是一个复杂而涉及多个领域知识的研究课题。
摘要:为促进区域综合能源系统(regional integrated energy system,RIES)集群的高比例新能源就地消纳,实施新能源的RIES内部消纳、RIES间互补消纳及氢能转换调节消纳策略,解决RIES多购售主体电能交易模式、氢能耦合高效应用和源荷不确定性调度风险等关键问题,提出了RIES集群的三阶段调度随机优化模型。第一阶段,基于电储能调节的RIES新能源电力波动平抑模型,提升电能质量。第二阶段,基于演化博弈的RIES间新能源互补交易调度模型,优化制定购电选择主体策略。第三阶段,采用电转氢及混氢技术,消纳互补交易后的过剩新能源,实现电能时移和电-气、电-热转移的氢能调节;考虑源荷不确定性的随机优化模型,获得兼顾经济性和鲁棒性的调度策略。通过仿真算例验证了方法的有效性。
这段摘要涉及到区域综合能源系统(RIES)集群中新能源的消纳问题,主要包括了解决多个关键问题的三阶段调度随机优化模型。让我们逐步解读:
-
背景和目标:
- 摘要的起始部分提到为了促进区域综合能源系统集群的高比例新能源就地消纳。这意味着有一个关注如何更有效地利用和整合新能源的问题。
-
调度策略的三个阶段: a. 第一阶段:
- 基于电储能调节的新能源电力波动平抑模型。这表明在第一阶段,采用电储能技术来平抑新能源电力波动,以提升电能质量。
b. 第二阶段:
- 基于演化博弈的新能源互补交易调度模型。这意味着在第二阶段,通过演化博弈的方式来优化不同综合能源系统之间的新能源互补交易,优化购电选择主体策略。
c. 第三阶段:
- 采用电转氢及混氢技术,消纳互补交易后的过剩新能源。这表明第三阶段主要涉及使用氢技术,将过剩的新能源转化为氢能,实现电能的时移和电-气、电-热转移的氢能调节。
-
调度模型的特点:
- 该模型考虑了源荷不确定性,使用随机优化模型来获得兼顾经济性和鲁棒性的调度策略。这表明在考虑能源系统中存在的不确定性情况下,采用了随机优化方法来制定具有经济性和鲁棒性的调度方案。
-
方法验证:
- 最后,通过仿真算例验证了该方法的有效性。这意味着作者通过模拟具体情境来证明他们提出的三阶段调度随机优化模型在实际情况中的有效性。
综合来看,这段摘要描述了一个针对区域综合能源系统集群中新能源就地消纳的研究,通过引入三阶段的调度随机优化模型来解决相关的关键问题,并通过仿真验证了该方法的有效性。
关键词:氢耦合区域综合能源系统;质子交换膜电解槽;点对点交易;演化博弈;条件风险价值;
-
氢耦合区域综合能源系统:
- 这个关键词表明涉及到将氢能源与区域综合能源系统相互整合的系统。可能包括使用氢能源作为能源系统的一部分,以实现更全面、高效的能源利用。
-
质子交换膜电解槽:
- 指的是一种电解槽技术,通常用于水电解制氢。在这里,质子交换膜电解槽可能是指使用质子交换膜作为电解槽的一部分,用于将水分解为氢气和氧气。
-
点对点交易:
- 这表示能源系统中的直接交易,可能是指能源的直接买卖,而不涉及中间环节。在这个背景下,可能涉及到直接的能源交易,例如从一个产生能源的点直接向另一个需要能源的点交易。
-
演化博弈:
- 这表明涉及到一个博弈论中的概念,可能是指在一段时间内各方策略的不断演变和调整。在能源系统中,演化博弈可能指的是各个参与者策略的动态变化和相互影响。
-
条件风险价值:
- 这个术语可能涉及到在一定条件下的风险价值评估。在能源系统的背景下,条件风险价值可能是指在特定条件下,特定能源系统或交易的风险价值。
这些关键词结合起来,似乎描述了一个涉及到氢能源的综合能源系统,可能包括质子交换膜电解槽技术的应用,采用点对点交易模式进行能源交易,并在其中考虑了演化博弈的动态和条件下的风险价值评估。这可能是一个研究能源系统中氢能源整合和交易模式优化的课题。
仿真算例:以西北某地区为例,选取 4 个 RIES 组成 RIES集群作为研究对象,其中 RIES2 为氢耦合 RIES。RIES2 的各元件参数及其他 RIES 的储能装置参数见附录 B 表 B1、B2;各 RIES 中的电、气、热负荷预测曲线见附录 B 图 B1;ADN 和天然气网的购、售电价格见附录 B 表 B3、B4[20]。取各 RIES 中的源荷数据计算得均值k ,并将 0.1k作为标准差m ,根据呈正态分布的预测误差生成场景集,采用概率距离削减法将场景集中的场景削减为 10 个典型场景,各场景的生成概率见附录 B 表 B5。设计了 4 种典型调度策略的算例情形进行仿真对比分析,验证本文方法的有效性及其优势。情形 1:不考虑源荷不确定性,不考虑氢耦合调节,集群内 4 个传统 RIES 进行本文三阶段优化调度,再通过系统内耦合设备实现异质能平衡。情形 2:考虑源荷不确定性,集群内有 3 个传统 RIES 和 1 个氢耦合 RIES,它们之间不进行电能售电交易,再通过各系统内的能源耦合设备平衡各自异质能,独自实现随机优化调度。情形 3:不考虑源荷不确定性,集群内 3 个传统 RIES 和 1 个氢耦合 RIES 进行本文三阶段优化调度,再通过系统内耦合设备实现异质能平衡。情形 4(本文方法):在情形 3 条件下,考虑源荷不确定性。
仿真程序复现思路:
这个问题涉及的仿真复现步骤和思路相当复杂,需要详细的数据和模型。以下是一种可能的思路和伪代码示例,但实际复现可能需要更多的详细数据和算法实现。
首先,我将尝试以伪代码的形式来表示这个仿真的思路,用一种简化的方式来表达:
第一阶段:电储能平抑新能源波动的优化模型
# 导入优化算法库
from optimization_library import FastNonDominatedSort
# 定义优化问题
def objective_function(x):
# 编写目标函数
# ...
# 设置算法参数
parameters = {
'population_size': 100,
'max_generations': 50,
# 其他参数
}
# 使用快速非支配多目标优化算法求解
result = FastNonDominatedSort(objective_function, parameters)
optimized_solution = result.run()
第二阶段:P2P 电能交易双层博弈模型
# 导入遗传算法库和Cplex求解器
from optimization_library import GeneticAlgorithm
from cplex_solver import CplexSolver
# 定义双层博弈模型
def p2p_game_model(x):
# 编写双层博弈模型
# ...
# 设置遗传算法参数
ga_parameters = {
'population_size': 50,
'max_generations': 30,
# 其他参数
}
# 使用遗传算法嵌套Cplex求解器求解
genetic_algorithm = GeneticAlgorithm(p2p_game_model, ga_parameters)
cplex_solver = CplexSolver()
result = genetic_algorithm.run(solver=cplex_solver)
optimized_strategy = result.get_optimal_strategy()
第三阶段:CVaR的氢耦合RIES优化调度模型
# 导入Yalmip工具箱和Cplex求解器
import yalmip
from optimization_library import CplexSolver
# 定义CVaR的氢耦合RIES优化调度模型
def cvar_ries_model(x):
# 编写CVaR的氢耦合RIES优化调度模型
# ...
# 设置优化器和求解器
optimizer = yalmip.Optimizer()
solver = CplexSolver()
# 使用Yalmip和Cplex求解器求解
optimizer.add_variable(x)
optimizer.add_constraint(cvar_ries_model(x) <= 0)
optimizer.set_objective(your_objective_function)
# 求解最优化问题
optimizer.solve(solver=solver)
optimized_schedule = optimizer.get_variable_value(x)
请注意,上述代码是伪代码,具体的实现细节和参数设置需要根据具体问题和使用的工具库进行调整。这里使用的库和工具是虚构的,你需要根据你的具体需求选择适当的库和工具。