神经网络常用激活函数详解
个人主页: https://zhangxiaoshu.blog.csdn.net
欢迎大家:关注+点赞+评论+收藏⭐️,如有错误敬请指正!
未来很长,值得我们全力奔赴更美好的生活!
前言
神经网络的激活函数是在每个神经元的输出上应用的非线性函数。激活函数的引入是为了给神经网络引入非线性特性,从而增强网络的表达能力,使其能够学习和表示更为复杂的关系。这篇文章主要介绍一些常见的神经网络激活函数,包括sigmoid、tanh、ReLU、Leoky ReLU、ReLU6和Softmax。
文章目录
- 前言
- 一 、sigmoid
-
- 1.表达式及其图像:
- 2. Sigmoid激活函数的优缺点:
- 3. 使用场景:
- 4. PyTorch代码:
- 二、tanh
-
- 1. 表达式以及图像:
- 2. Tanh激活函数的优缺点:
- 3. 使用场景:
- 4. PyTorch代码:
- 三、ReLU
-
- 1.表达式及其图像:
- 2. ReLU激活函数的优缺点:
- 3. 使用场景:
- 4. PyTorch代码:
- 四、Leoky ReLU
-
- 1.表达式及其图像:
- 2. Leoky ReLU激活函数的优缺点:
- 3. 使用场景:
- 4. PyTorch代码:
- 五、ReLU6
-
- 1.表达式及其图像:
- 2. ReLU6激活函数的优缺点:
- 3. 使用场景:
- 4. PyTorch代码:
- 六、Softmax
-
- 1.表达式及其图像:
- 2. Softmax激活函数的优缺点:
- 3. 使用场景:
- 4. PyTorch代码:
- 总结
一 、sigmoid
1.表达式及其图像:
Sigmoid激活函数是一种常用的非线性激活函数,通常用于神经网络的输出层,特别是在二分类问题中。其主要特点是将输入值映射到一个在 (0, 1) 范围内的输出,其数学表达式为:
σ ( x ) = 1 1 + e − x \sigma(x)=\frac{1}{1+e^{-x}} σ(x)=1+e−x1
其中, e e e 是自然对数的底。函数的图像呈 S 形曲线,中心点在 x = 0 x=0 x=0 处,输出值在 x x x接近正无穷和负无穷时分别趋近于 1 和 0。
2. Sigmoid激活函数的优缺点:
优点:
- 输出范围在 (0, 1): Sigmoid函数的输出范围在 (0, 1) 之间,可以被解释为概率值,特别适用于二分类问题,如判断一个样本属于某一类的概率。
- 平滑性: Sigmoid函数是光滑的、可导的函数,这在梯度下降等优化算法中很有用。
缺点:
- 梯度消失问题:Sigmoid函数在输入非常大或非常小的情况下,导数接近于零,可能导致梯度消失问题。在深度网络中,这可能影响训练的稳定性和速度。
- 输出非零均值: Sigmoid的输出均值接近于 0.5,这会导致下一层神经元得到的输入主要是正值,可能影响权重的更新效率。
- 计算复杂度:Sigmoid函数的计算涉及到指数运算,相对于一些计算简单的激活函数(如ReLU),计算复杂度较高。
3. 使用场景:
-
二分类问题:Sigmoid通常用于二分类问题的输出层,输出可以解释为样本属于某一类别的概率。 -
概率表示:当需要将神经网络的输出解释为概率值时,Sigmoid是一个合适的选择。 -
输出范围限制:在需要将输出限制在 (0, 1) 范围内的情况下,如图像生成等任务,Sigmoid可以确保输出在指定范围内。
尽管Sigmoid在过去被广泛使用,但由于其存在的梯度消失问题和其他缺点,近年来在深度学习中,一些其他激活函数如ReLU及其变体更受青睐。选择激活函数通常取决于具体的任务和网络结构。
4. PyTorch代码:
import torch
import torch.nn.functional as F
x = torch.randn(5, 5)
sigmoid_output = torch.sigmoid(x)
二、tanh
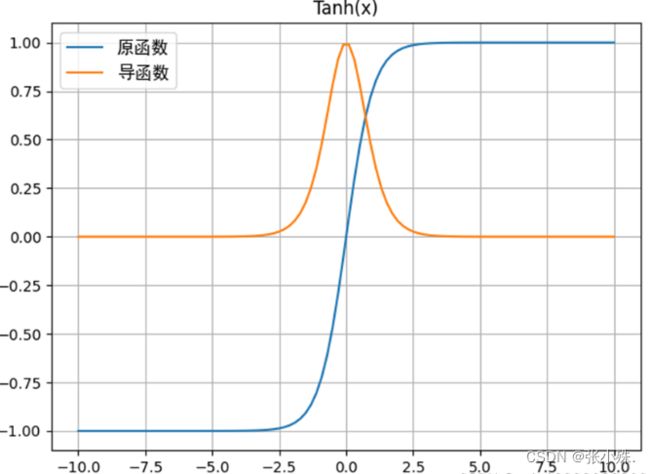
1. 表达式以及图像:
Tanh(双曲正切)激活函数是一种常用的非线性激活函数,其输出范围在 (-1, 1) 之间。其数学表达式为:
t a n h ( x ) = e x − e − x e x + e − x tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}} tanh(x)=ex+e−xex−e−x
Tanh函数在形状上类似于Sigmoid函数,但其输出范围更广,从 -1 到 1,均值接近于 0。与Sigmoid相比,Tanh对输入的响应更强烈,可以更好地处理具有负值的输入。
2. Tanh激活函数的优缺点:
优点:
-
归一化输出: Tanh的输出范围在(-1, 1)之间,相比于Sigmoid的(0, 1),输出更接近于零均值,有助于减小梯度消失问题,提高模型的训练稳定性。
-
激活强度较大: Tanh对输入的响应相对更强烈,这有助于模型学习更复杂的特征和表示,使其在某些任务上比Sigmoid更有效。
-
零中心化: Tanh的输出均值接近零,有助于减小下一层神经元接收到的输入的均值,有助于提高网络的拟合能力。
缺点:
-
梯度消失问题: 虽然相对于Sigmoid,Tanh缓解了梯度消失问题,但仍然可能在深度网络中存在。对于极端值的输入,Tanh函数的导数仍然会趋近于零。
-
计算复杂度: Tanh函数的计算同样涉及到指数运算,相对于一些计算简单的激活函数(如ReLU)而言,计算复杂度较高。
3. 使用场景:
-
中间层的激活函数:Tanh通常在神经网络的中间层中使用,特别是在循环神经网络(RNN)等结构中,有助于处理具有正负值的输入。 -
具有零均值要求的场景:当输入数据有零均值要求时,Tanh激活函数可能更适用,因为它的输出均值接近零。 -
二分类问题:在二分类问题中,Tanh可以用作输出层的激活函数,尤其是当输出需要在 (-1, 1) 范围内表示时。
总体而言,Tanh激活函数在某些场景下可以取代Sigmoid,并且相对于Sigmoid来说,具有更广的输出范围和更强的响应能力。然而,使用时需要注意梯度消失问题以及计算复杂度。在深度学习中,ReLU及其变体目前是更为常见的选择之一。
4. PyTorch代码:
import torch
import torch.nn.functional as F
x = torch.randn(5, 5)
tanh_output = torch.tanh(x)
三、ReLU
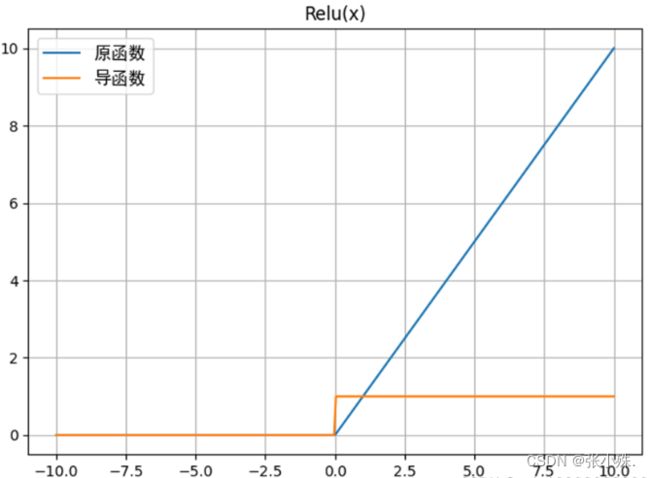
1.表达式及其图像:
ReLU(Rectified Linear Unit)是一种常用的非线性激活函数,其数学表达式为:
f ( x ) = m a x ( 0 , x ) f(x)=max(0,x) f(x)=max(0,x)
即,对于输入 x x x,如果 x x x 大于零,输出为 x x x;否则,输出为零。ReLU函数是一个简单而有效的激活函数,它在神经网络中被广泛使用。其特点是在正值区域上保持线性增长,同时在负值区域上输出为零。
2. ReLU激活函数的优缺点:
优点:
-
计算简单: ReLU函数的计算非常简单,只需要一个阈值比较和取最大值的操作,相比于Sigmoid和tanh等函数的指数运算,计算速度更快。
-
稀疏激活性: ReLU激活函数在正值区域上保持线性增长,有助于网络的稀疏激活性,即只有少数神经元被激活,使网络更加稀疏。
-
解决梯度消失问题: 相比于Sigmoid和tanh等激活函数,ReLU在正值区域上没有梯度饱和问题,可以缓解梯度消失问题,有助于训练深度网络。
缺点:
-
死亡神经元问题: 在训练过程中,某些神经元可能永远不会被激活,称为“死亡神经元”问题。如果某个神经元在训练过程中对于所有样本都是负的,那么该神经元的权重将永远不会被更新。
-
不适合所有情况: 对于一些数据分布特殊的任务,ReLU可能表现不佳。例如,在处理负值较多的数据时,可能导致大量神经元死亡。
3. 使用场景:
-
深度神经网络:ReLU在深度神经网络中广泛应用,特别是在卷积神经网络(CNN)和循环神经网络(RNN)等结构中,因为它有助于解决梯度消失问题。 -
计算资源受限的环境:由于ReLU的计算简单,适用于资源受限的环境,例如移动设备、嵌入式系统等。 -
稀疏激活性要求:当稀疏激活性是一个设计考虑因素时,ReLU是一个合适的选择,因为它更容易使网络保持稀疏性。
总体而言,ReLU是深度学习中常用的激活函数之一,尤其在解决梯度消失问题和提高计算效率方面表现优越。然而,需要注意一些可能出现的问题,如死亡神经元问题。在实际应用中,有时会采用ReLU的变体(如Leaky ReLU等)以缓解一些潜在问题。
4. PyTorch代码:
import torch
import torch.nn.functional as F
x = torch.randn(5, 5)
relu_output = F.relu(x)
四、Leoky ReLU
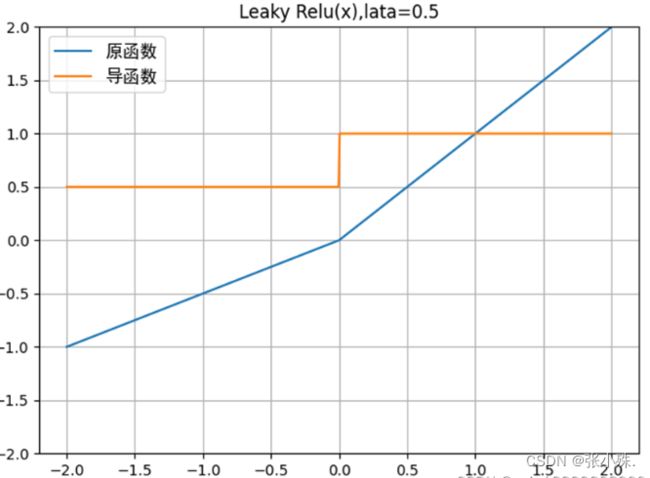
1.表达式及其图像:
Leaky ReLU是对标准ReLU激活函数的一种改进,旨在解决ReLU中可能出现的“死亡神经元”问题。Leaky ReLU允许在负值区域有一个小的斜率,而不是直接输出零。其数学表达式为:
f ( x ) = { x , if x > 0 α x , if x ≤ 0 f(x)=\left\{\begin{array}{ll} x, & \text { if } x>0 \\ \alpha x, & \text { if } x \leq 0 \end{array}\right. f(x)={x,αx, if x>0 if x≤0
其中, α \alpha α是一个小的正数,通常很小,比如 0.01。Leaky ReLU保留了负值区域,这有助于避免某些神经元在训练中变得“死亡”。
图像如下所示:
2. Leoky ReLU激活函数的优缺点:
优点:
-
避免死亡神经元问题: Leaky ReLU允许在负值区域有一个小的斜率,这有助于保持负值区域的梯度,避免神经元在训练过程中变得“死亡”。
-
简单计算: 与ReLU相比,Leaky ReLU的计算仍然相对简单,只需添加一个额外的斜率。
-
稀疏激活性: Leaky ReLU保持了一定的稀疏激活性,即仍然有神经元保持非零输出。
缺点:
-
不一定适用于所有情况: 尽管Leaky ReLU解决了死亡神经元问题,但它并不一定在所有任务中都表现得比标准ReLU更好。在某些数据分布下,Leaky ReLU可能仍然存在一些问题。
-
选择斜率的问题: 选择 α \alpha α的值通常是一个超参数,需要进行调优。选择不当可能导致一些问题,过小的 α \alpha α可能无法解决死亡神经元问题,而过大的 α \alpha α可能导致Leaky ReLU失去ReLU的优势。
3. 使用场景:
-
深度神经网络:Leaky ReLU在深度神经网络中被广泛应用,尤其是在解决死亡神经元问题方面。 -
需要稀疏激活性:当需要保持一定的稀疏激活性时,Leaky ReLU可以是一个合适的选择。 -
不确定数据分布:在处理不同数据分布的任务时,Leaky ReLU可能是一个更健壮的激活函数选择,相对于ReLU在某些情况下可能表现得更好。
总体而言,Leaky ReLU是对标准ReLU的一种改进,通过引入一个小的负斜率解决了死亡神经元问题。在实际应用中,可以根据具体任务和数据分布选择合适的激活函数。
4. PyTorch代码:
import torch
import torch.nn.functional as F
x = torch.randn(5, 5)
leaky_relu_output = F.leaky_relu(x, negative_slope=0.01) # 可根据需求调整负斜率
五、ReLU6
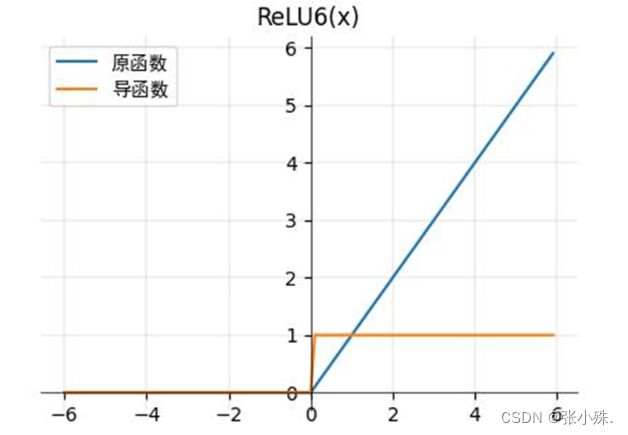
1.表达式及其图像:
ReLU6(Rectified Linear Unit 6)是对ReLU的一种变体,它在正值区域上仍然保持线性增长,但在负值区域上截断,并将负值限制在零以下。其数学表达式为:
f ( x ) = m i n ( m a x ( 0 , x ) , 6 ) f(x)=min(max(0,x),6) f(x)=min(max(0,x),6)
即,对于输入 x x x,如果 x x x大于零,输出为 x x x;如果 x x x 小于等于零,输出为零;如果 x x x大于6,输出为6。ReLU6的主要特点是在负值区域上的截断,将负值限制在零以下,并且在正值区域上允许线性增长,最大值限制为6。
图像如下所示:
2. ReLU6激活函数的优缺点:
优点:
-
抑制过大的激活值: 通过将激活值限制在6以下,ReLU6有助于抑制激活值的过大增长,使得网络的表示范围更受控制,尤其是在计算资源受限的环境中使用低精度的时候也能有很好的数值分辨率
(低精度的Float 16 / INT 8无法很好地精确大范围的数值)。 -
计算简单: 类似于ReLU,ReLU6的计算仍然相对简单,只需要比较和取最小值和最大值的操作。
缺点:
- 不适用于所有场景: ReLU6在一些任务和数据分布上可能表现不佳。对于一些特定的任务,可能有更适合的激活函数选择。
3. 使用场景:
-
限制激活值范围:当需要限制激活值的范围,避免过大的激活值对网络造成负面影响时,ReLU6可以作为一种选择。 -
计算资源受限的环境:由于ReLU6的计算仍然相对简单,适用于计算资源受限的环境,例如移动设备、嵌入式系统等。 -
对输入范围有要求的任务:当输入数据有特定的范围要求时,ReLU6可以用来限制输出在一个固定的范围内。
总体而言,ReLU6是对ReLU的一种变体,主要通过将激活值限制在6以下来抑制激活值的过大增长。在实际应用中,选择激活函数通常要根据具体的任务和网络结构进行调整。
4. PyTorch代码:
import torch
import torch.nn.functional as F
x = torch.randn(5, 5)
relu6_output = F.relu6(x)
六、Softmax
1.表达式及其图像:
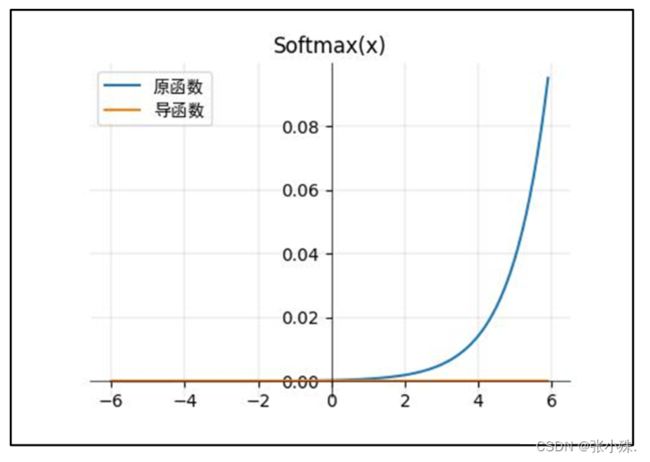
Softmax激活函数是一种常用于多分类问题的激活函数。它接受一个实数向量作为输入,并将其转换成一个概率分布。Softmax函数的数学表达式为:
S o f t m a x ( z ) i = e z i ∑ j = 1 K e z j Softmax(z)_i=\frac{e^{z_{i} }}{ {\textstyle \sum_{j=1}^{K}} e^{z_{j} }} Softmax(z)i=∑j=1Kezjezi
其中, z z z是输入向量的元素, K K K是类别的总数。Softmax函数对输入向量进行指数运算,然后进行归一化,使得输出的各个元素表示对应类别的概率,且概率之和为1。
图像如下所示:
2. Softmax激活函数的优缺点:
优点:
-
概率表示: Softmax将输入映射为概率分布,适用于多分类问题,输出的各个元素可以解释为对应类别的概率。
-
可导性: Softmax是可导的,这使得在使用梯度下降等优化算法进行训练时更容易处理。
缺点:
-
对输入敏感: Softmax对输入的敏感性较高,当输入中存在较大的值时,指数运算可能导致数值溢出(数值过大)或数值不稳定的问题。
-
类别之间相关性: Softmax假设各个类别是独立的,可能无法很好地处理类别之间的相关性。
-
标签不平衡: 在处理标签不平衡的情况下,Softmax可能导致模型更加关注样本较多的类别,而对样本较少的类别学习不足。
3. 使用场景:
-
多分类问题:Softmax主要用于解决多分类问题,其中需要将输入映射为各个类别的概率分布。 -
输出层激活函数:Softmax通常作为神经网络输出层的激活函数,特别适用于需要将网络输出解释为概率分布的场景。 -
需要概率表示的任务:当任务需要模型输出概率表示时,例如图像分类、语音识别等,Softmax是一个常用的选择。
总体而言,Softmax激活函数在多分类问题中表现出色,提供了一种将神经网络输出转换为概率分布的方式。然而,在一些特殊情况下,可能需要注意其对输入的敏感性以及类别之间的相关性问题。
4. PyTorch代码:
import torch
import torch.nn.functional as F
x = torch.randn(5, 5)
softmax_output = F.softmax(x, dim=1)
总结
在深度学习中,激活函数的选择对模型的性能和训练过程至关重要。以下是以上6种激活函数的简单总结及其使用建议:
Sigmoid激活函数:输出范围在 (0, 1),适用于二分类问题,但容易导致梯度消失问题。适用于二分类问题的输出层,不建议在隐藏层使用,可以考虑其他更有效的激活函数。
Tanh激活函数: 输出范围在 (-1, 1),零中心化,相对缓解了梯度消失问题。适用于隐藏层,特别是需要输出在 (-1, 1) 范围的任务。
ReLU激活函数:简单计算,解决了梯度消失问题,但可能导致死亡神经元问题。在隐藏层中广泛使用,特别适用于深度神经网络和计算资源受限的环境。
Leaky ReLU激活函数: 解决了死亡神经元问题,保持了稀疏激活性。用于隐藏层,尤其是在ReLU表现不佳时可以考虑使用,需要保持稀疏激活性的任务。
Softmax激活函数: 输出表示概率分布,适用于多分类问题。用于多分类问题的输出层,将网络输出映射为概率分布,例如图像分类、语音识别等。
ReLU6激活函数:对激活值进行限制,抑制过大的激活值。用于需要限制激活值范围的任务,例如计算资源受限的环境。
- 在
隐藏层,通常首选ReLU及其变体,如Leaky ReLU,因为它们计算简单且在实践中表现良好。 - 对于
二分类问题,Sigmoid仍然是一个合适的选择,但要注意梯度消失问题。 - 对于
需要输出概率分布的多分类问题,Softmax是一个自然的选择。 根据任务和实验结果,可以进行激活函数的调整和尝试,选择最适合特定情况的激活函数。
参考和图片来源:
小wu学cv:常用的激活函数合集(详细版)