算法设计与分析复习

ch1 绪论

算法：有穷性、确定性、能行性、有输入、有输出

ch2 数学基础

复杂性函数的阶

阶为复杂性函数的主导项
同阶函数 f(n)=θ(g(n))
∃c1 c2 >0 对∀n>n0 有 c1g(n)≤f(n)≤c2g(n)
保证高阶项相同即可 渐进紧界
低级函数 f(n)=O(g(n)) 渐进上界
高阶函数 f(n)=Ω(g(n)) 渐进下界

master定理

ch3 分治法

分治法的设计步骤

分解：将原问题划分为一些子问题，子问题与原问题形式一样（以便递归求解），只是规模更小
解决：递归的求解子问题，如果子问题的规模足够小则停止递归，直接求解
合并：将子问题的解组合为原问题的解
有时要求解与原问题形式不完全一样的问题，我们将这种情况看成合并的一部分

最大子数组问题

输入：数组A[]
输出：数组A的最大子数组
分治思想：为了求救数组A[]的最大子数组，我们把A[]从中间分成两部分 A的最大子数组就只有三种情况：在mid左，在mid右，跨过mid，前两个是原问题的子问题，第三个不是，所以我们需要解决第三个问题，解决后，即可很容易的完成此问题

最大值最小值问题

输入：数组A
输出：A的最大值和最小值
把A分成两部分，找这两部分中的Max和Min （递归情况）
直到划分后的数组大小为2或1（基本情况）

中位数（第i大的数）问题

输入：数组A
输出：数组A的中位数
分解：把A数组分解成若干的子数组，子数组的规模一般可以取5
找到这若干个子数组中位数
合并：求出若干子数组中位数的中位数，并按照此中位数m对数组A进行划分，小于m的在左，大于m的在右，划分后m的下表为k
如果k=i，返回A[k]
如果k>i，在左面那部分选择第i大的数
如果k

ch4 动态规划

设计步骤

1.刻画一个最优解的结构特征
2.递归的定义最优解的值
3.计算最优解的值，通常采用自底向上的方法
4.利用计算出的信息构造一个最优解

最优子结构
问题的最优解由相关子问题的最优解组合而成，而这些子问题可以独立求解
例：钢条切割问题中，把长度为n的钢条第一次切割后，出现两段钢条，原钢条的最大收益可由第一次切割后两段钢条的最大收益相加得到，且这两段钢条的最大收益可以独立求解
用反证法证明最优子结构

重复子问题
在问题的求解过程中很多子问题的解被重复使用

矩阵链乘问题—划分动态规划

1.分析优化解（最优解）结构—原问题最优解由子问题最优解组合而成、子问题最优解可以独立计算。在本题中Ai…j=Ai…k×Ak+1…j
可以说明重叠子问题
2.递归定义最优解
自底向上，按照最优解的结构进行定义

3.计算最优代价
自底向上进行计算，确定计算m[i,j]需要访问哪些表项

n=p.length-1
let m=[1..n,1..n] and s[1..n-1,2..n]be new table
for i=1 to n 
     m[i,i]=0 // 对角线上元素初始化为0
for l =2 to n
     for i =1 to n-l+1
           j=i+l-1
           m[i,j]=∞
           for k=i to j-1
           q=m[i,k]+m[k+1,j]+pi-1pkpj
           if q ＜m[i,j]
                m[i,j]=q
                s[i,j]=k

4.构造最优解

时间复杂性：三层循环，每层最多n次 O（n^3）

最长公共子序列问题—前缀动态规划

注意：只要求出现顺序相同，不要求连续出现
1.分析优化解结构

2.递归定义最优解
输入是两个串，为了刻画其特征，我们需要一个二维矩阵C[i,j]
根据优化子结构，写出其递归式

3.计算最优解即LCS的长度，自底向上

初始化i=0或j=0时，C[i,j]=0后，按行计算C[i,j]
为了刻画最优解，我们仍需一个矩阵B存储信息，存储指针表明每步的选择

递归的打印，因为首先出现的是LCS最后面的元素

时间复杂性 O（mn）

0-1背包

问题定义：给定n种物品和一个背包，物品i的重量是wi，价值vi，背包容量为C, 问如何选择装入背包的物品，使装入背包中的物品的总价值最大？

1.优化子结构
对一个物品，我们有选或者不选两个选择，所以从原问题，到原问题的子问题，我们进行的选择是第一个物品选或者不选，所以子问题就是选第一个物品，即容量被重新定义，不选第一个物品，容量无需更新，这两种情况下，收益较高的那种，即

2. 递归定义最优解
建立递归方程

3.自底向上计算最优解

ch5 贪心算法

设计步骤

1.将最优化问题转化为这样的形式：对其做出一次选择后，只剩下一个子问题要求解
2.证明做出贪心选择后，原问题总是存在最优解，即贪心选择总是安全的
3.证明做出贪心选择后，剩余的子问题满足性质：其最优解与贪心选择组合后即可得到原问题的最优解，这样就得到了最优子结构

贪心选择性
我们可以通过做出局部最优（贪心）选择来构造全局最优解。
与动态规划不同，贪心算法再做出第一次选择前不求解任何子问题，贪心算法通常是自顶向下的，进行一次又一次的选择从而使子问题的规模越来越小

最优子结构
一个问题的最优解包含子问题的最优解
在贪心算法中，只需证明：将子问题最优解与贪心选择组合在一起可以构成原问题的最优解

任务安排问题

贪心思想： 每次选择结束时间最早的活动

哈夫曼编码

贪心思想： 每次选择出现频率最低的两个字符作为左右儿子构造编码树

ch6 树搜索

基础–深度优先与广度优先

广度优先–利用队列先进先出、后进后出

深度优先–利用栈后进先出

爬山法

深度优先搜索中，经常遇到多个节点可扩展，爬山法用启发式测度来排序节点扩展的顺序
即框架与深度有优先相同，显示根确定的单元素栈S，如果栈顶时目标节点停止，否则弹出栈顶S,S的子节点按照其启发式测度由大到小的顺序压入S

例：8-puzzle问题

用错误位置的方块数定义启发式函数

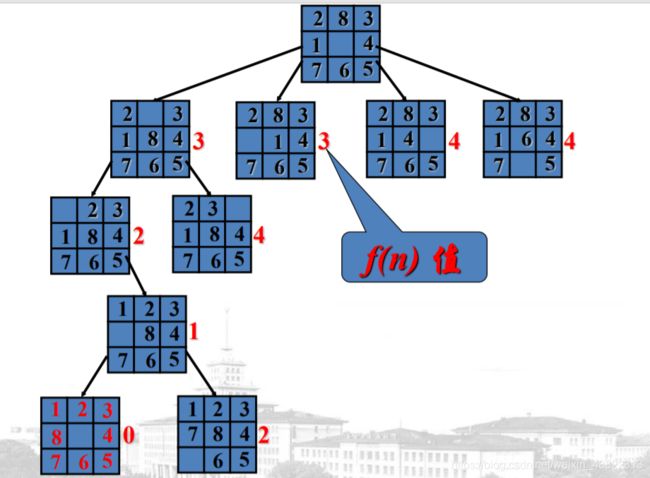
所以定义启发式测度函数是爬山法的关键，该函数决定了搜索的顺序，我们要找离我们想找的东西更近似的答案，以他作为新的起点进行搜索

Best-First

在目前产生的所有节点中，选择有最小评价函数值的节点进行扩展
具有全局优化观念，爬山法仅有局部优化的观念
每次选的不是当前路径的，而是所有节点中有最小评价函数值的节点

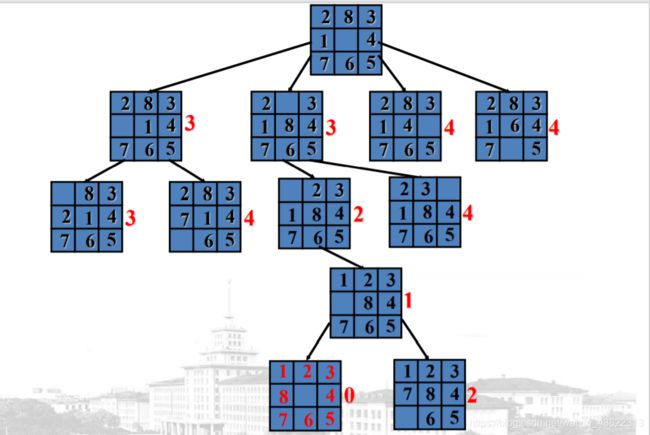
此处的评价函数与爬山法解决此问题时的启发式测度函数相同

分支界限

利用上述策略找到一个界限，利用此界限剪除不可能优化的分支，从而降低搜索的时间复杂度

拓扑排序
依次选择没有父亲的节点，把它删掉

用分支界限解决问题的例子

人员安排问题

输入

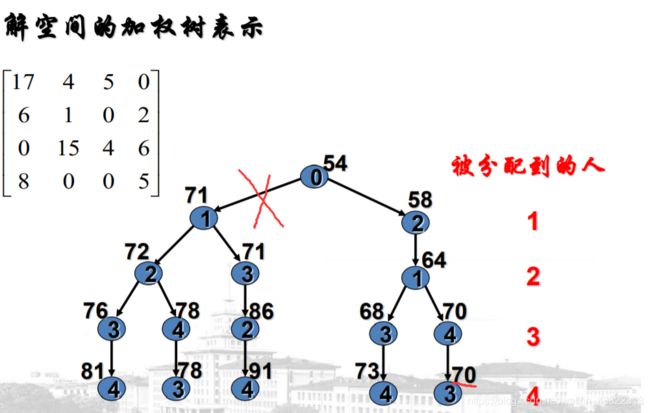
问题的解空间：所有可能的拓扑排序序列生成的二叉树

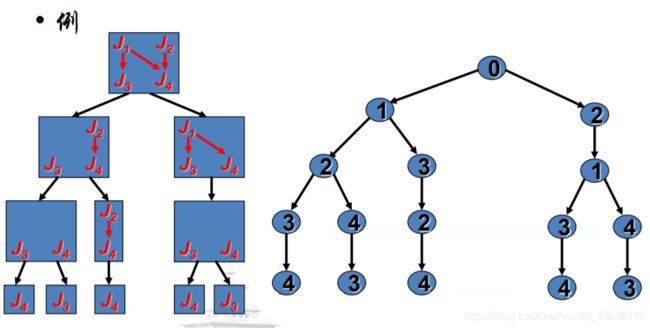
处理代价矩阵，得到更好的下界，从而更容易剪枝

旅行商问题

问题描述：无向连通图，非负加权边，寻找一条从任意节点开始，经过每个节点一次，最后返回开始节点的路径，且路径的代价（加权和）最小。

利用边来划分，即某条边是否在我们所选的路径中，从而得到二叉树，从而每次剪枝可以剪掉1/2而不是1/n

剪枝策略为：不断发现优化解的上界a，从而一旦有子节点的代价下界超过a，则终止该结点的扩展

所以类似于上面的人员分配问题，我们首先处理代价矩阵

为了实现上述剪枝策略，我们选处理后为代价（即路径长）为0的变中，去掉此边后，从此边所在位置的行和列中各选一个最小值–即如果不选这个边ij则必有一个从i出去的边（在行中）也必有一个进入j的边（在列中）选取他们的和最小，即为下界

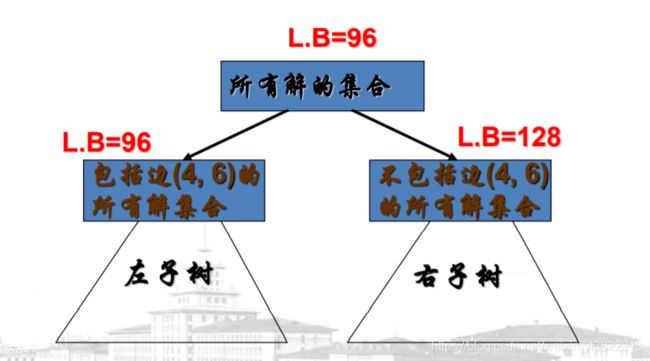
递归的构造左右子树
其中左子树包含的边所在行列去掉，ji设为∞
如果更改后存在行或列不含0，则减去最小得到0，并更新左子树下界

右子树ij设为无穷
如果更改后存在行或列不含0，则减去最小得到0，并更新右子树下界

递归的继续做，得到可行解后 剪枝

A*算法

分支界限算法的关键是界限，有了界限就可以剪枝，但是不知道什么时候获得最优解
A算法的核心是在某些情况下，我们得到的解一定是最优解因此算法可以停止
利用best-first搜索策略
关键–代价函数
对于任意节点n：g(n)=从树根到n的代价，h(n)=从n到目标结点的优化路径代价，f*(n)=g(n)+h*(n)是经过结点n到达目标结点的代价。

由于h*(n)是我们不知道的，我们只需要保证：

1. 使用任何方法去估计h*(n), 用h(n)表示h*(n)的估计
2. h(n)≤h*(n)总成立
3. f(n)=g(n)+h(n)≤g(n)+h*(n)=f*(n)定义为n的代价

以最短路径问题为例

可以理解为保守的估计h*(n)从而保证一旦获得解即为最优解

使用best-first策略进行扩展
到结束时，所有可扩展点中T的代价时最小的，从而肯定为最优解

ch7 平摊分析

关注一系列操作上的时间复杂度

聚集方法

证明对所有n，一个n个操作的序列最坏情况下花费的总时间为T(n)
所以所有操作有相同的平摊代价T(n)/n

从更加广义的角度，取看待操作序列的某些性质：比如栈操作中，栈为空n个操作最多有n个元素入栈，比如二进制计数器+1操作中，n次操作，第n位最多变换n/(2的n次幂) 次

会计方法

一个操作序列中有很多不同的操作，不同类型的操作代价可能不同，我们为每个操作分配一个平摊代价，只要保证“存款”（每次操作积累的多余）总是>0，那么n次操作的平摊代价的和就是n次操作总的代价的上界
例如，在栈操作中，push的平摊代价设为2，pop的平摊代价设为0，multipop的平摊代价也设为0，因为栈中的元素个数总是>=0的，即栈中没有元素时不能进行pop和multipop操作，所以可以保证我们的“存款”总是>=0的
二进制计数器中，0->1设平摊代价为2，1->0设平摊代价为0，因此我们的“存款”即为计数器中1的个数，始终>=0 所以所有翻转操作的平摊代价和是这个操作序列代价的上界

势能方法

方法引入
在会计方法中，我们把余额与数据对象相连，在势能方法中我们把余额与整个数据结构关联，所有的余额的和构成势能

设计思想
首先保证势函数在D0处为0，其余情况势函数大于0 则总的平摊代价就是总的实际代价的一个上界
在较昂贵操作前，势能应该较大，经历昂贵操作后，势变到最小，在后面的操作中再逐渐提高势能
可以考虑在一系列操作中，是哪个操作花费时间较高，那这个操作引起的某个量的变化就可能作为势
例如在栈操作中，用栈中元素个数作为势能，保证了势能始终>=0
具体分析每个操作，每个操作的平摊代价=实际代价+势能差

动态表—3n

动态表用数组实现，每当数组装满时，重新分配一个大小为原数组两倍大的数组。
聚集分析

会计方法

势能方法

ch8 网络流–最大流和最小割

最大流问题
在不违反任何流量限制下，计算出从源点s运送物料到汇点t的最大速率
流网络
G=（V,E）是一个有向图，图中每个边(u,v)∈E，有一个容量c(u,v)≥0
如果存在边(u,v)则不存在其反向边(v,u)
每个结点都在从s到t的路径上
G中的流是一个实值函数 f：V×V->R 满足：
容量限制
对所有的结点u,v 都有0≤f(u,v)≤c(u,v)
流量守恒
流入=流出

增广路径：从s到t的一条简单（不含环）路径

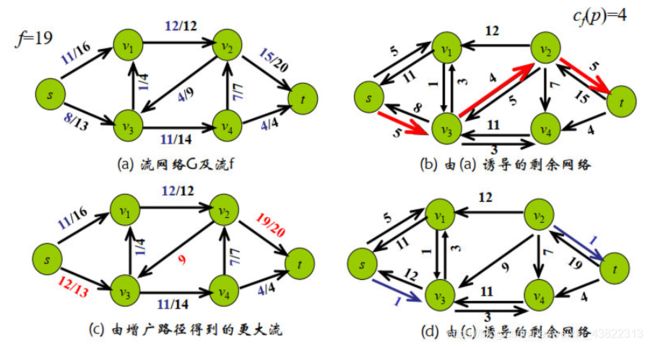
残余网络
残余网络（余图）中的一个流给我们指出的是一条路线图：如何在原
来的流网络中增加流

算法过程：
对随便选取的一条从s到t的路径创建余图，余图与原图点集相同，边的
大小取决于c(uv)边的容量和f(uv)当前此边的流量有关，正向边等于前者
减去后者（如果减完大于0）否则没有，反向边等于f(uv)
在此余图中继续寻找一条s到t的路径，按上述规则更新余图，直到找不
到s到t的一条路径算法结束
如果选择的不好可能找不到最大流
一个流是最大流当且仅当其残余网络（余图）不包含任何增广路径

时间复杂度
时间O(mC) C是最大流的值，所以C是最多的迭代次数 m是边数

流网络的切割
为了知道在算法终止时是否找到了最大流，引入网络流中的切割概念

最小割：网络流中容量最小的切割

切割：把结点分成S和T=V-S S包含s，T包含t，（S,T）的容量c(S,T)是
从u属于S到v属于T的所有边uv的容量之和

有定理 对给定流f，横跨任何切割的净流量都等于|f|

最大流最小割定理
1.f是G的一个最大流
2.残存网络（余图）不包含任何增广路径
3.|f|=c(S,T)，其中（S,T）是流网络的某个切割
123等价

二分图匹配：使用最大流算法
加入一个源s和一个汇t

ch9 字符串匹配

Rabin-karp算法

分析

KMP算法

前缀函数


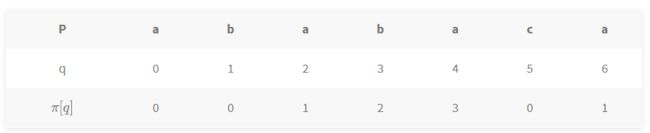
分析：
最差运行时间O（n+m）
计算前缀表：O（m）
主算法O（n）

BMH算法

逆向匹配
思想：不匹配的概率总是更大的