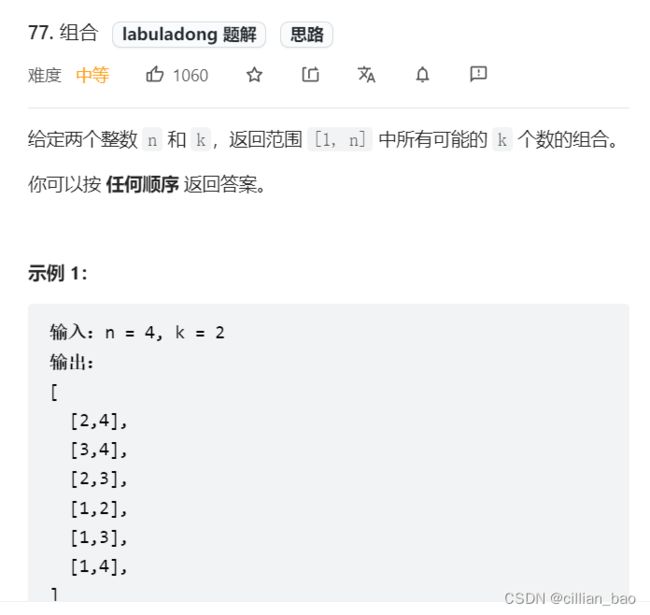
回溯算法详解之排列组合
一、前言
回溯算法本质上是递归函数在不同条件下的运作。程序自动进行压栈与出栈的操作,从细节上来说比较难理解(可以结合IDE按步调试去理解)。回溯算法、深度优先遍历、递归这三者的共同点都在于先进后出。
回溯法的本质:采用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现,在反复重复上述的步骤后可能出现两种情况:
找到一个可能存在的正确的答案;
在尝试了所有可能的分步方法后宣告该问题没有答案。
回溯算法中强调选择与选择列表,在选择列表中每一步要操作的元素叫做选择,已经操作过的叫做路径。
在真正做回溯算法的时候,千万不能进入死胡同,对于其中的每一步细节进行分析,因为我们的脑子压不了几个栈,除非一笔一划写在纸上,记录每一步的状态以及所有与其相关的变量,让其回溯得时候跳到相应得状态时有相应的状态作为依据。
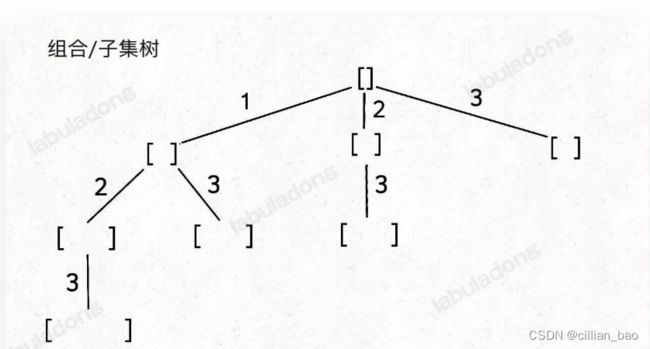
二、序列的排列、组合、子集生成问题
按照给定数组中的元素是否存在重复的值,是否可以重复选择可以将排列、组合、子集的生成问题进行分类。
分类的具体情况如下:
- 无重复值不可复选
- 有重复值不可复选
- 无重复值可复选
以上的三种分类与排列、组合、子集问题形成笛卡尔积,共有9种不同的类型。再加上在此大框架下的各种限制条件,所以能够形成很多种问题。
对于解决上面的问题,最重要的是能够画出回溯树并在树的基础上合理的剪枝。
其实在代码中,我们最多需要考虑的问题是我们的代码好像没有显式的递归结束条件,会不会进入死循环,其实不会,一旦进入不了for循环,也就没有了递归,递归也就自动结束了。
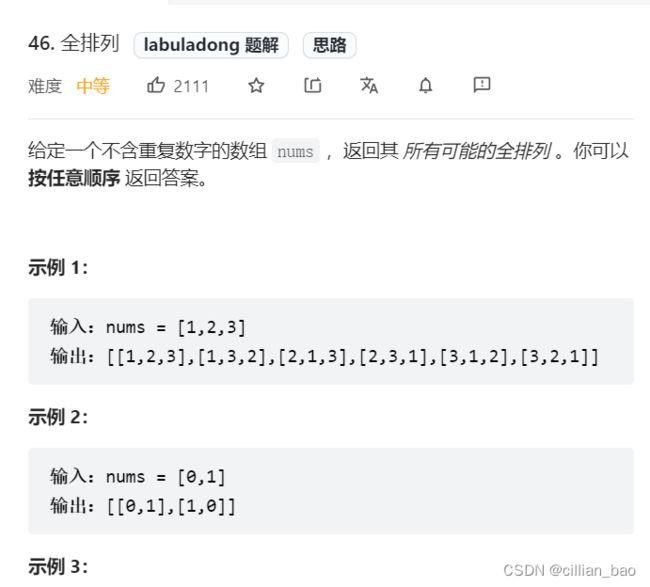
1. 无重复不可复选的排列问题
全排列
class Solution {
List<List<Integer>> ret=new LinkedList<>();
public List<List<Integer>> permute(int[] nums) {
boolean [] used=new boolean[nums.length];
LinkedList<Integer> track=new LinkedList<>();
backtrack(nums,used,track);
return ret;
}
public void backtrack(int []nums,boolean []used,LinkedList<Integer> track)
{
if(track.size()==nums.length)
{
ret.add(new LinkedList(track));
}
for(int i=0;i<nums.length;i++)
{
if(used[i])
{
continue;
}
track.add(nums[i]);
used[i]=true;
backtrack(nums,used,track);
used[i]=false;
track.removeLast();
//下面的也可
//track.remove(track.size()-1);
}
}
}
从这个简单的全排列中可以学习到的是整个回溯算法的核心框架
for 选择 in 选择列表
选择是否合法判断
做选择
将选择从选择列表中移除
路径中添加选择
回溯
撤销选择
路径中删除该选择
将该选择加入选择列表
值得注意的是在全排列这道题中,对于将选择从选择列表中移除这一步,我们采用了偷懒的做法,使用标记数组完成这一步。
代码中的一个需要注意的点:add(new LinkedList(track)),由于Java语言的特性
2、 无重复不可复选的子集问题

在排列问题提取出来的回溯算法的基础上,对于子集问题,额外需要考虑的就是其中的无序性。[2,1]与[1,2]一样,[1,2,3]与[3,1,2]一样等等。那样怎么样保证其无序性,重点在于其中元素的有序。我们使得取值的时候永远是从前向后取就可以。
class Solution {
List<List<Integer>> ret=new LinkedList<>();
public List<List<Integer>> subsets(int[] nums) {
LinkedList<Integer> track=new LinkedList<>();
backtrack(nums,0,track);
return ret;
}
public void backtrack(int []nums,int index, LinkedList<Integer> track)
{
ret.add(new LinkedList<>(track));
for(int i=index;i<nums.length;i++)
{
track.add(nums[i]);
backtrack(nums,i+1,track);
track.removeLast();
}
}
}
在代码中,我们利用了index参数控制树枝的生长避免产生重复的子集。
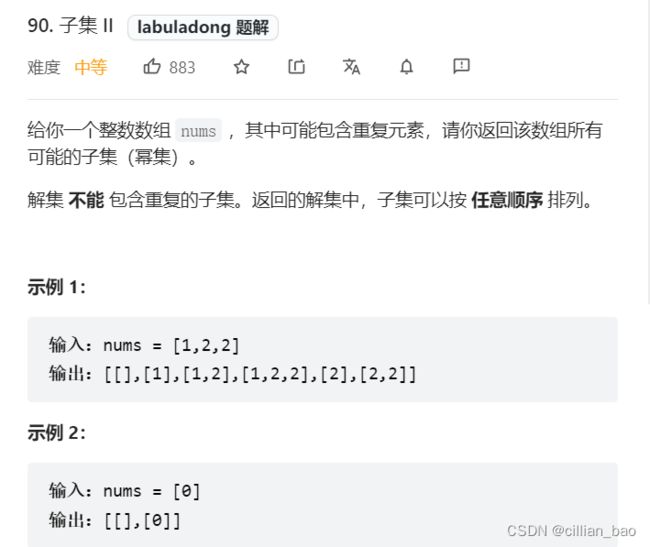
3、有重复值不可复选的子集问题
这道题在无重复不可复选的子集基础上加了一个限制条件,起初我认为这样的限制条件是没有用的,但是通过实践发现,确实会造成重复的问题。后来我想到的解决方法是在将track容器加入ret中的时间,利用List容器的contains方法判断是否有重复的,这个时候需要我们对contains方法有清晰的了解,它内部的原理是调用相应的equals方法进行判断。而对于List的equals方法十分苛刻,需要list的长度、以及各个位置上的元素相等。

所以对于这道题来说,我们正好用contains这样的方法来解决。
class Solution {
List<List<Integer>> ret=new LinkedList<>();
public List<List<Integer>> subsetsWithDup(int[] nums) {
LinkedList <Integer> track=new LinkedList<>();
Arrays.sort(nums);
backtrack(nums,0,track);
return ret;
}
public void backtrack(int []nums,int index,LinkedList<Integer> track)
{
if(!ret.contains(track))
{
ret.add(new LinkedList<>(track));
}
for(int i=index;i<nums.length ;i++)
{
track.add(nums[i]);
backtrack(nums,i+1,track);
track.removeLast();
}
}
}
那么我们联想我们之前在数组的双指针题目中我们做过一道题叫做
删除有序数组中的重复项。其实这道题有借鉴这种去重的思想,就是数组中如何去重。要先排序,后用双指针。
按照上面的理论,我们的代码可以写为:
class Solution {
List<List<Integer>> ret=new LinkedList<>();
public List<List<Integer>> subsetsWithDup(int[] nums) {
LinkedList <Integer> track=new LinkedList<>();
Arrays.sort(nums);
backtrack(nums,0,track);
return ret;
}
public void backtrack(int []nums,int index,LinkedList<Integer> track)
{
ret.add(new LinkedList<>(track));
for(int i=index;i<nums.length ;i++)
{
if (i > index && nums[i] == nums[i - 1])
{
continue;
}
track.add(nums[i]);
backtrack(nums,i+1,track);
track.removeLast();
}
}
}
注意,上面的剪枝条件只有在回溯的时候才会有用
if (i > index && nums[i] == nums[i - 1])
{
continue;
}
遍历一遍数组的时候,其中的所有值都会进入track中,并且由于进入ret没有判断条件,ret中会依次有[],[1],[1,2],[1,2,2]并且这些都不会触发nums[i]==nums[i-1]的比较,因为他们的index都等于i。只有在回溯的时候出现i>index的情况,才会进行剪枝。这个剪枝的时刻发生在当我们”归“到track中只剩下[1,2]的时候,这个时候其实i=1,我们返回到track.removeLast()这一步,并且将2删除,只剩下1,这时候进入for循环i+1=2,那么这时候我们将重复的2看作2’,这时候如果没有nums==nums[i-1]的限制,那么就会出现将2‘加入track中,然后再次进入for循环将track=[1,2’]加入ret中,就会出现重复;另外必须有i>inex的限制存在,因为我们在“递”的情况下,是都要的,如果没有这个限制,则[1,2,2’]会被认为是不符合条件的。
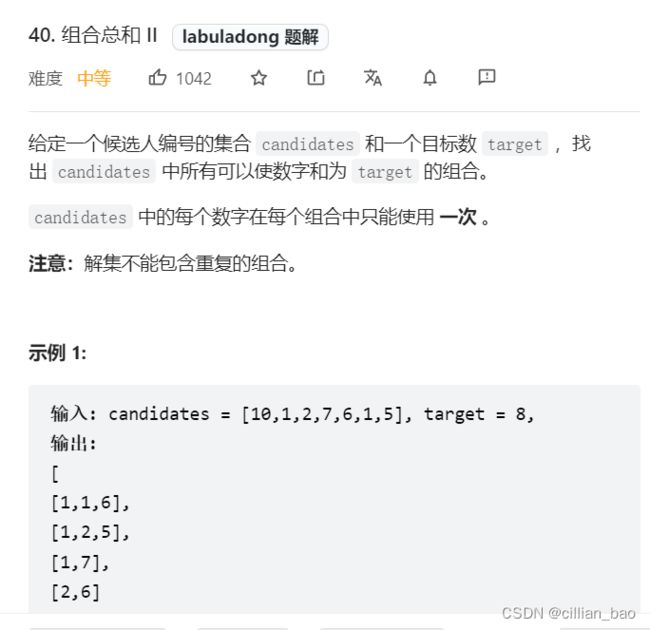
4、带限制条件的有重复值不可复选的组合问题
这道题逻辑十分简单,在有重复值的子集题目基础上,我们只需要加一个限制条件,track中的数字和=target即可。
方法1:自治List的求和函数
class Solution {
List<List<Integer>> ret=new LinkedList<>();
LinkedList<Integer> track=new LinkedList<>();
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
backtrack(candidates,target,0);
return ret;
}
public void backtrack(int []candidates,int target,int index)
{
if(listsum(track)==target)
{
ret.add(new LinkedList<>(track));
// return;
}
for(int i=index;i<candidates.length;i++)
{
if(i>index && candidates[i]==candidates[i-1])
{
continue;
}
track.add(candidates[i]);
backtrack(candidates,target,i+1);
track.removeLast();
}
}
public int listsum(LinkedList<Integer> track)
{
Iterator iter=track.iterator();
int sum=0;
while(iter.hasNext())
{
sum+=(int)iter.next();
}
return sum;
}
}
方法2:利用trackSum记录路径上的和
class Solution {
List<List<Integer>> ret=new LinkedList<>();
LinkedList<Integer> track=new LinkedList<>();
int trackSum=0;
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
backtrack(candidates,target,0);
return ret;
}
public void backtrack(int []candidates,int target,int index)
{
if(trackSum==target)
{
ret.add(new LinkedList<>(track));
return;
}
if(trackSum>target)
{
return;
}
for(int i=index;i<candidates.length;i++)
{
if(i>index && candidates[i]==candidates[i-1])
{
continue;
}
track.add(candidates[i]);
trackSum+=candidates[i];
backtrack(candidates,target,i+1);
track.removeLast();
trackSum-=candidates[i];
}
}
}
5、 有重复元素不可复选的排列问题
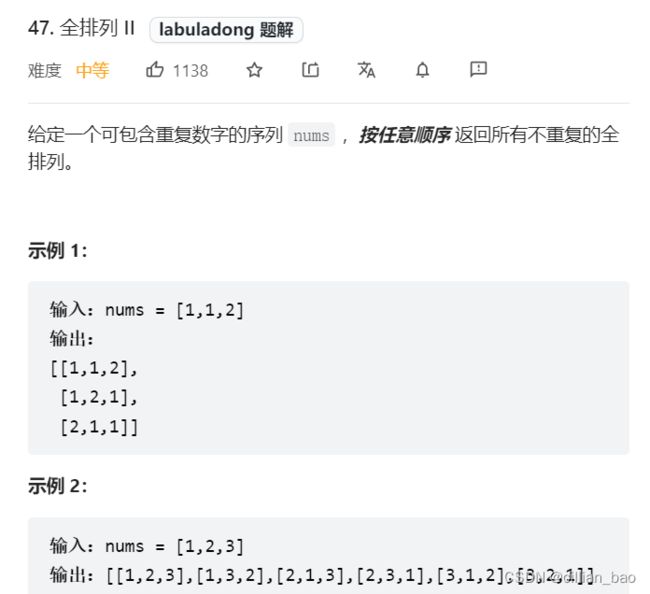
这道题我一开始拿到的时候,我认为和有重复值不可复选的组合问题,剪枝条件一样,主要的问题就是把for循环的初始条件改一下,把前面的index换成0并且增加used标记数组不就行了,但是发现我们的结果是错的,拿到的ret中为空,原因在于我们在排列问题中向ret加入的条件为
track中的数目等于nums的长度。因为里面有重复值,如果我们简单的利用nums[i]==nums[i-1]进行剪枝,那么track中的数目永远都不会达到nums的长度。
原因在于这样的剪支条件不是不够,而是太强,需要我们额外的削弱,我们使用used[i-1]进行保证,让其
原理:标准全排列算法之所以出现重复,是因为把相同元素形成的排列序列视为不同的序列,但实际上它们应该是相同的;而如果固定相同元素形成的序列顺序,当然就避免了重复。当出现重复元素时,比如输入 nums = [1,2,2’,2’‘],2’ 只有在 2 已经被使用的情况下才会被选择,同理,2’’ 只有在 2’ 已经被使用的情况下才会被选择,这就保证了相同元素在排列中的相对位置保证固定。
class Solution {
List<List<Integer>> res = new LinkedList<>();
LinkedList<Integer> track = new LinkedList<>();
boolean[] used;
public List<List<Integer>> permuteUnique(int[] nums) {
// 先排序,让相同的元素靠在一起
Arrays.sort(nums);
used = new boolean[nums.length];
backtrack(nums);
return res;
}
void backtrack(int[] nums) {
if (track.size() == nums.length) {
res.add(new LinkedList<>(track));
return;
}
for (int i = 0; i < nums.length; i++) {
if (used[i]) {
continue;
}
// 新添加的剪枝逻辑,固定相同的元素在排列中的相对位置
if (i > 0 && nums[i] == nums[i - 1] && !used[i-1]) {
continue;
}
track.add(nums[i]);
used[i] = true;
backtrack(nums);
track.removeLast();
used[i] = false;
}
}
}
组合(带限制条件的组合问题)
class Solution {
List<List<Integer>> ret=new LinkedList<>();
public List<List<Integer>> combine(int n, int k) {
//有无序,又有限制
LinkedList<Integer> track=new LinkedList<>();
backtrack(n,1,track,k);
return ret;
}
public void backtrack(int n,int index,LinkedList<Integer> track,int k)
{
if(track.size()==k)
{
ret.add(new LinkedList<>(track));
}
for(int i=index;i<=n;i++)
{
track.add(i);
backtrack(n,i+1,track,k);
track.removeLast();
}
}
}
分割回文串(带限制条件的组合问题)

这道题经过上面的几道题对框架的提炼以及对基本限制条件怎么写的学习,我们基本对这道题有个思路,但是实际操作过程中不知道怎么处理“分割”这个动作,我的第一思路是使用StringBuilder进行辅助操作,应该说是能做的。但是对于分割线的最好办法是做substring,这样能够通过下标控制分割的字符。
class Solution {
List<List<String>> ret=new LinkedList<>();
public List<List<String>> partition(String s) {
LinkedList<String> track=new LinkedList<>();
backtrack(s,0,track);
return ret;
}
public void backtrack(String s,int index,LinkedList<String> track)
{
//判断是否把所有的字符都遍历了一遍,如果是,那么这个track中肯定是一个正确答案。
if(index>=s.length())
{
ret.add(new LinkedList<>(track));
}
for(int i=index;i<s.length();i++)
{
if(check(s,index,i))
{
track.add(s.substring(index,i+1));
}
//一定要有下面的跳过,否则没有加上的也会在后面delete
else {
continue;
}
backtrack(s,i+1,track);
track.removeLast();
}
}
//这个回文串的判断相对来说,比较简单一些,运用了双指针的技巧
public boolean check(String s,int start,int end)
{
for(int i=start,j=end;i<j;i++,j--)
{
if(s.charAt(i)!=s.charAt(j)) {
return false;
}
}
return true;
}
}
分割线的理解,index是上一层已经确定了的分割线,i是这一层试图寻找的新分割线。
首先在递归还没有进入归的时候,会把单个字符逐一的加到track后,当进入归后,则会扩大分割字串的范围,使得寻找完所有的可能情况。
其实上面的在回溯算法中进行回文串的判断,时间复杂度相当的高。所以我们可以尝试用不同的方法进行优化。
解法2:动态规划优化回文串判断+回溯
class Solution {
List<List<String>> ret=new LinkedList<>();
LinkedList<String> track=new LinkedList<>();
public List<List<String>> partition(String s) {
int n=s.length();
boolean [][]dp=new boolean[n][n];
for(int i=0;i<n;i++)
{
Arrays.fill(dp[i],true);
}
//只有1个字符的时候肯定是回文的
for(int i=0;i<n;i++)
{
dp[i][i]=true;
}
//因为判断s(i,j),i必须小于等于j,所以我们只需要对右上角进行赋值判断
for(int i=n-1;i>=0;i--)
{
for(int j=i+1;j<n;j++)
{
//本质上这是一种中心扩散的方式从中心向外扩散
dp[i][j]=dp[i+1][j-1] && (s.charAt(i)==s.charAt(j));
}
}
backtrack(s,0,track,dp);
return ret;
}
public void backtrack(String s,int index,LinkedList<String> track,boolean [][]dp)
{
//有一个值得注意的点就是怎么样我能认为,其完成了
if(index>=s.length())
{
ret.add(new LinkedList<>(track));
}
for(int i=index;i<s.length();i++)
{
if(dp[index][i])
{
track.add(s.substring(index,i+1));
}
else{
continue;
}
backtrack(s,i+1,track,dp);
track.removeLast();
}
}
}
注意上面的对于二维dp数组的初始化为true很重要,因为我们在遍历右上角元素的时候会用到右下角的元素来计算出相应的值,举个例子:
dp[1][2]=dp[2][1]&&(s.charAt(1)==s.charAt(2))
用到了dp[2][1],这是因为我们的遍历方式的问题。我们可以采取对角线依次遍历的方式解决。
解法3:记忆化搜索+回溯
这个做法的时间复杂度并没有降低,只是换了一种思路,将整个字符串的各种可能的分割结果,这些结果是不是回文串的判断保存在了一个二维数组中。
class Solution {
int[][] dp;
List<List<String>> ret = new ArrayList<List<String>>();
List<String> track = new ArrayList<String>();
int n;
public List<List<String>> partition(String s) {
n = s.length();
dp= new int[n][n];
dfs(s, 0);
return ret;
}
public void dfs(String s, int i) {
if (i == n) {
ret.add(new ArrayList<String>(track));
return;
}
for (int j = i; j < n; ++j) {
if (isPalindrome(s, i, j) == 1) {
track.add(s.substring(i, j + 1));
dfs(s, j + 1);
track.remove(track.size() - 1);
}
}
}
// 记忆化搜索中,f[i][j] = 0 表示未搜索,1 表示是回文串,-1 表示不是回文串
public int isPalindrome(String s, int i, int j) {
if (dp[i][j] != 0) {
return f[i][j];
}
if (i >= j) {
dp[i][j] = 1;
} else if (s.charAt(i) == s.charAt(j)) {
dp[i][j] = isPalindrome(s, i + 1, j - 1);
} else {
dp[i][j] = -1;
}
return dp[i][j];
}
}
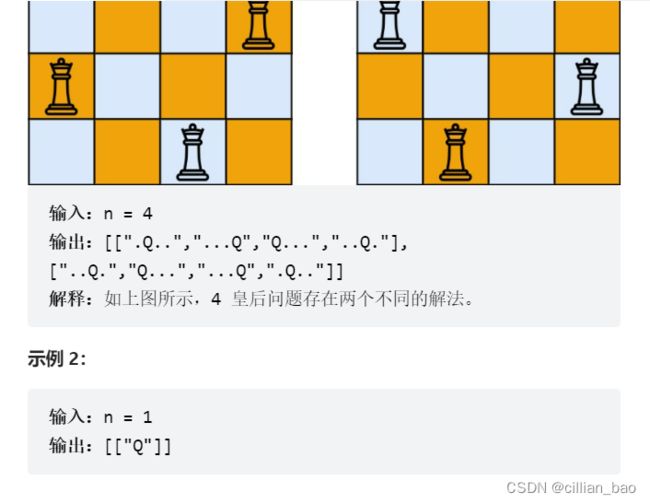
N皇后(带限制条件的排列问题)
class Solution {
List<List<String>> ret=new LinkedList<>();
public List<List<String>> solveNQueens(int n) {
List<String> track=new LinkedList<>();
StringBuilder sb=new StringBuilder();
for(int i=0;i<n;i++)
{
sb.append(".");
}
for(int i=0;i<n;i++)
{
track.add(sb.toString());
}
backtrack(0,track,n);
return ret;
}
public void backtrack(int row,List<String> track,int n)
{
if(row==n)
{
ret.add(new LinkedList<>(track));
}
for(int col=0;col<n;col++)
{
if(!isValid(row,col,track))
{
continue;
}
StringBuilder sb=new StringBuilder(track.remove(row));
sb.replace(col,col+1,"Q");
track.add(row,sb.toString());
backtrack(row+1,track,n);
StringBuilder sbu=new StringBuilder(track.remove(row));
sbu.replace(col,col+1,".");
track.add(row,sbu.toString());
}
}
public boolean isValid(int row,int col,List<String> track)
{
//同一
int n=track.size();
//同一列
for(int i=0;i<row;i++)
{
if(track.get(i).charAt(col)=='Q')
{
return false;
}
}
for(int i=row-1,j=col-1;i>=0 && j>=0;i--,j--)
{
if(track.get(i).charAt(j)=='Q')
{
return false;
}
}
for(int i=row-1,j=col+1;i>=0 && j<n;i--,j++)
{
if(track.get(i).charAt(j)=='Q')
{
return false;
}
}
return true;
}
}
子集划分问题
3、划分为k个相等的子集

这个问题本质上拿来我是没有思路的,不知道怎么做。这道题不是传统意义上的排列组合问题,而是套壳的排列组合问题。
在我们的思路中一道真正的排列组合问题的场景如下:有n个小球与k个桶,每个桶里装一个小球,有多少种方法?我们假设这种排列组合问题的符号表达为P(n,k)
这道题可以分为两种不同的视角:
视角1:从球的视角去看,每个球可以选择k个桶中的任意一个,那么第一个球的选择有两种,第一种是入桶,入桶的话,第一个球有k个选择,剩下n-1个球,可以用剩下的k-1个桶进行考虑,种类有kP(n-1,k-1)。第二种是不入桶,不入桶的话,是用剩下的n-1个球将k个桶装满,种类有p(n-1,k).故问题的总答案为kP(n-1,k-1)+p(n-1,k)。
视角二:从桶的视角来把握,这个视角比较简单,因为每个桶都要装满,不会出现,上面的进入不进入的问题,所以问题的答案显而易见的为n*p(n-1,k-1)。
有了上面的排列组合题目作为铺垫,那么可以将次问题可视化为桶和球的问题,比如说,题目中的k个子集就可以看作k个桶,那么将nums中的数装入到k个桶中,并且满足一定的限制条件(每个桶中的数的和一致)。
同样的,这道题可以有两个视角去做,第一种从数的视角去做,第二种从桶的角度去做。
两种思路,可能导致截然不同的解题效果。两者都需要考虑一个数进入一个桶中就不能进入另一个桶中。
视角1:从数的角度
回溯算法,回溯算法能不能用for循环去做呢?其实这个问题就是在说,递归能不能都用for循环去做,有的for循环是可以的,有的for循环是不行的
class Solution {
public boolean canPartitionKSubsets(int[] nums, int k) {
if(k>nums.length)
{
return false;
}
int sum=0;
for(int num:nums)
{
sum+=num;
}
if(sum%k!=0)
{
return false;
}
int [] bucket=new int[k];
return backtrack(nums,bucket,0,sum/k);
}
boolean backtrack(int [] nums,int [] bucket,int index,int target)
{
if(index==nums.length)
{
for(int i=0;i<bucket.length;i++)
{
if(bucket[i]!=target)
{
return false;
}
}
return true;
}
for(int i=0;i<bucket.length;i++)
{
if(bucket[i]+nums[index]>target)
{
continue;
}
if(i > 0 && bucket[i] == bucket[i-1]){
continue;
}
bucket[i]+=nums[index];
if(backtrack(nums,bucket,index+1,target))
{
return true;
}
bucket[i]-=nums[index];
if(bucket[i]==0)
{
return false;
}
}
return false;
}
}
视角2:从桶的视角去看
从代码的角度去看的话,最大的不同是代码中出现了两次递归的调用,第一次在一个桶满转移到下一个桶时,第二次在同一个桶中选择下一个数字时。由于两次递归的存在,故我们需要对
nums中的数字进行标记,防止两次递归时都使用了同一个数字,那样就造成了一个数字出现在两个桶中,引起这个问题的本质在于我们在转移到下一个桶时,不知道数组中的数字应该从那个开始,我们确实也无法得知这时候数组中的具体清况,所以还是从0开始,并且额外使用标记数组used[i]防止一个数字装入多个桶中。
为了更进一步加快代码的剪枝效果,我们使用备忘录的方法,去除不必要的回溯,比如说现在
一个数组为nums=[1,2,3,4,4,6],k=4,那么每个桶中的和应该是5,但是我们可以发现最终是无法凑出来的,但是回溯算法会怎么买解决这个问题呢?会先将1,4放入第一个桶,再将2,3放入第二个桶,然后下去发现不行,回溯后,会将2,3放入第一个桶,1,4放入第二个桶,后面发现还是不行,再来,依次不行之后,最终返回false。但是我们发现上面的第一个桶和第二个桶完全属于相同的情况,所以我们需要每一保存状态,每一次判断状态,有相应的状态之后直接返回即可。
class Solution {
HashMap<Integer,Boolean> map=new HashMap<>();
public boolean canPartitionKSubsets(int[] nums, int k) {
//特殊情况的处理
if(k>nums.length)
{
return false;
}
int sum=0;
for(int ele:nums)
{
sum+=ele;
}
if(sum%k!=0)
{
return false;
}
int used=0;
return backtrack(0,k,0,nums,sum/k,used);
}
//下面的代码就表示第k个桶在当前循环中
public boolean backtrack(int bucket,int k,int index,int []nums,int target,int used)
{
if(k==0)
{
return true;
}
if(bucket==target)
{
boolean res=backtrack(0,k-1,0,nums,target,used);
map.put(used,res);
return res;
}
if(map.containsKey(used))
{
return map.get(used);
}
for(int i=index;i<nums.length;i++)
{
if (((used >> i) & 1) == 1) { // 判断第 i 位是否是 1
// nums[i] 已经被装入别的桶中
continue;
}
if(bucket+nums[i]>target)
{
continue;
}
bucket+=nums[i];
used |= 1 << i; // 将第 i 位置为 1
if(backtrack(bucket,k,i+1,nums,target,used))
{
return true;
}
// 撤销选择
used ^= 1 << i; // 使用异或运算将第 i 位恢复 0
bucket-=nums[i];
}
return false;
}
}
值得一提的是我们在代码中使用了位图的概念,使用一个数used答题了used数组。