5. 树与二叉树
考纲内容
（多考选择题，偶尔涉及树遍历相关的算法题）
- 树的基本概念
- 二叉树
- 二叉树的定义及其主要特征
- 二叉树的顺序存储结构和链式存储结构
- 二叉树的遍历
- 线索二叉树的基本概念和构造
- 树、森林
- 树的存储结构
- 森林与二叉树的转换
- 树和森林的遍历
- 树与二叉树的应用
- 二叉排序树
- 平衡二叉树
- 哈夫曼树和哈夫曼编码
1. 树的基本概念
- 性质
- 树的结点数等于所有结点的度数加1
- 度为m的树中第i层上至多有 m i − 1 m^{i-1} mi−1个结点（i ≥ \ge ≥ 1）
- 高度为h的m叉树至多有 m h − 1 m − 1 \frac{m^h-1}{m-1} m−1mh−1个结点，至少有h个结点
- 具有n个结点的m叉树的最小高度为 ⌈ l o g m ( n ( m − 1 ) + 1 ) ⌉ \lceil log_m(n(m-1)+1) \rceil ⌈logm(n(m−1)+1)⌉，最大高度为n-m+1
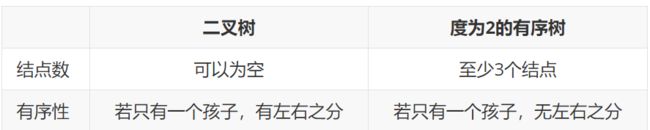
2. 二叉树
1. 二叉树的定义及其主要特性
- 特性
- 二叉树是有序树，左右子树不可颠倒
- 区别
2. 几个特殊的二叉树
- 满二叉树
- 定义：高度为h，且含有 2 h − 1 2^h-1 2h−1个结点的二叉树
- 特点
- 只有最后一层有叶子结点
- 不存在度为1的结点
- 按层序编号（1开始），编号为i的结点
- 若有双亲，则为 ⌊ i 2 ⌋ \lfloor \frac{i}{2} \rfloor ⌊2i⌋
- 若有左孩子，则为2i
- 若有右孩子，则为2i+1
- 所在层次(深度)为 ⌊ l o g 2 i ⌋ + 1 \lfloor log_2i\rfloor+1 ⌊log2i⌋+1
- 完全二叉树
- 定义：高为h、有n个结点的二叉树，其每个结点都与高度为h的满二叉树中编号为1~n的结点一一对应
- 特点
- 若 i > n 2 i > \frac{n}{2} i>2n，则结点i为叶子结点，否则为分支结点
- 叶子结点只可能在最后两层出现
- 最多只有一个度为1的结点
- 按层序编号后，若编号为i的结点为叶子结点或只有左孩子，则大于i的结点均为叶子结点
- n为奇数，每个分支结点都有左右孩子；n为偶数，编号为 n 2 \frac{n}{2} 2n结点只有左孩子
- 二叉排序树
- 定义：左子树上所有结点的关键字均小于根结点的关键字；右子树上的所有结点的关键字均大于根结点的关键字；左子树和右子树又各是一棵二叉排序树
- 平衡二叉树
- 定义：树上任一结点的左子树和右子树的深度之差不超过1
3. 性质（重点）
- （非空二叉树）叶子结点数 = 度为2的结点数+1，即 n 0 = n 2 + 1 n_0 = n_2 +1 n0=n2+1且 n 0 + n 2 n_0+n_2 n0+n2必为奇数， n 1 n_1 n1=1或0
- 第k层最多有 2 k − 1 2^{k-1} 2k−1个结点（ k ≥ 1 k \ge 1 k≥1）
- 高度为h的二叉树最多有 2 h − 1 2^h-1 2h−1个结点（ h ≥ 1 h \ge 1 h≥1）
- 具有n个结点的完全二叉树的高度为 ⌈ l o g 2 ( n + 1 ) ⌉ \lceil log_2(n+1)\rceil ⌈log2(n+1)⌉或 ⌊ l o g 2 n ⌋ + 1 \lfloor log_2n\rfloor+1 ⌊log2n⌋+1
- 二叉树的前、中和中、后两对遍历序列都可以唯一确定一棵二叉树，而前、后遍历序列不能唯一确定
4. 存储结构
1. 顺序存储结构
- 定义：用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素
- 注意
- 从数组下标1开始存储结点，不存在的结点可用0区分
2. 链式存储结构
- 注意
- 含有n个结点的二叉链表中，含有n+1个空链域
- 存储结构
typedef struct BTNode { ElemType data; struct BTNode *lchild, *rchild; }BTNode;
3. 二叉树的遍历和线索二叉树
1. 二叉树的遍历
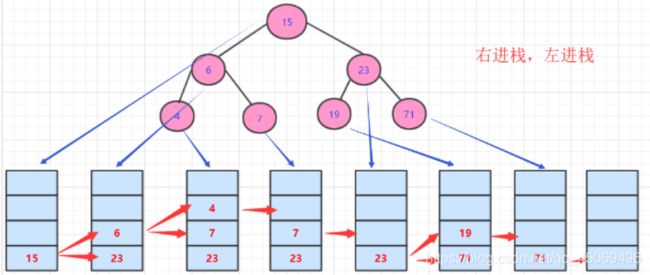
1. 先序遍历（PreOrder）
-
步骤
- 访问根结点
- 先序遍历左子树
- 先序遍历右子树
-
算法实现
- 递归实现
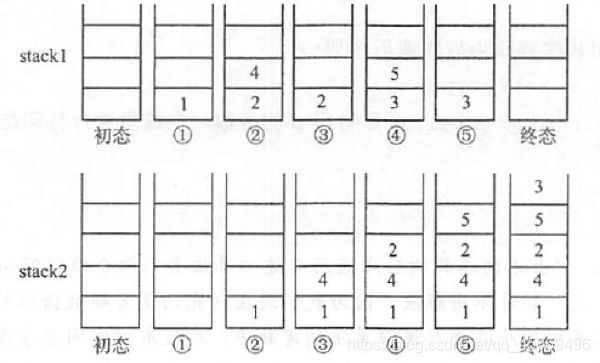
void PreOrder(BTNode *T) { if(T != NULL) { visit(T); PreOrder(T->lchild); PreOrder(T->rchild); } }- 非递归实现
void PreOrderNonrecursion(BTNode *bt) { if(bt != NULL) { BTNode *Stack[maxSize]; //定义一个栈 int top = -1; //初始化栈 BTNode *p; Stack[++top] = bt; //根结点入栈 while(top != -1) //栈空循环退出，遍历结束 { p = Stack[top--]; //出栈并输出栈顶结点 visit(p); if(p->rchild != NULL) //右孩子存在，则入栈 Stack[++top] = p->rchild; if(p->lchild != NULL) //左孩子存在，则入栈 Stack[++top] = p->lchild; } } }
2. 中序遍历（InOrder）
-
步骤
- 中序遍历左子树
- 访问根结点
- 中序遍历右子树
-
算法实现
- 递归实现
void InOrder(BTNode *T) { if(T != NULL) { InOrder(T->lchild); visit(T); InOrder(T->rchild); } }- 非递归实现
void InOrderNonrecursion(BTNode *bt) { if(bt != NULL) { BTNode *Stack[maxSize]; int top = -1; BTNode *p; p = bt; while(top != -1 || p != NULL) { while(p !=NULL) //左孩子存在，则入栈 { Stack[++top] = p; p = p->lchild; } if(top != -1) { p = Stack[top--]; visit(p); p = p->rchild; } } } }
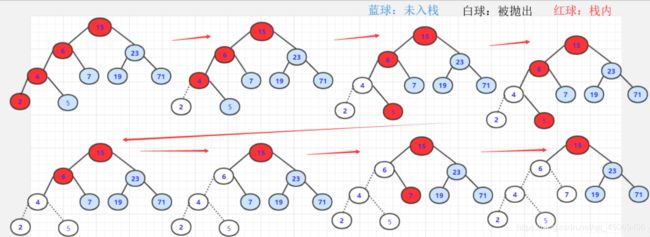
3. 后序遍历（PostOrder）
- 步骤
- 后序遍历左子树
- 后序遍历右子树
- 访问根结点
- 算法实现
- 递归实现
void PostOrder(BTNode *T) { if(T != NULL) { PostOrder(T->lchild); PostOrder(T->rchild); visit(T); } }- 非递归实现
void PostOrder(BTNode *T) { if(bt != NULL) { BTNode *Stack1[maxSize]; int top1 = -1; BTNode *Stack2[maxSize]; int top2 = -1; BTNode *p = NULL; Stack1[++top1] = bt; while(top1 != -1) { p = Stack1[top--]; Stack2[++top2] = p; if(p->lchild != NULL) Stack1[++top1] = p->lchild; if(p->rchild != NULL) Stack2[++top2] = p->rchild; } while(top2 != -1) //出栈序列即为后序遍历序列 { p = Stack2[top2--]; visit(p); } } }
4. 层次遍历
- 算法思想：建立一个循环队列，将二叉树头结点入队，然后出队，访问该结点，若它有左子树，则将左子树的根结点入队；若它有右子树，则将右子树的根结点入队。然后出队，访问出队结点。重复直到队空。
- 算法实现
void level(BTNode *p) { int front, rear; BTNode *que[maxSize]; //定义一个循环队列，用来记录将要访问的层次上的结点 front = rear = 0; BTNode *q; if(p != NULL) { rear = (rear + 1) % maxSize; que[rear] = p; //根结点入队 while(front != rear) //队列不空的时候进行循环 { front = (front + 1) % maxSize; q = que[front]; //队头结点出队（front指向队头元素前一个位置） visit(q); if(q->lchild != NULL) //左子树不空，则其根结点入队 { rear = (rear + 1) %maxSize; que[rear] = q->lchild; } if(q->rchild != NULL) //右子树不空，则其根结点入队 { rear = (rear + 1) %maxSize; que[rear] = q->rchild; } } } }
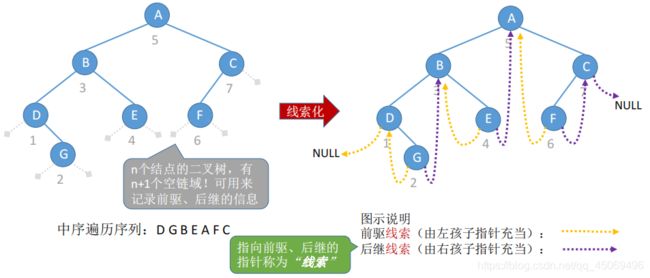
2. 线索二叉树
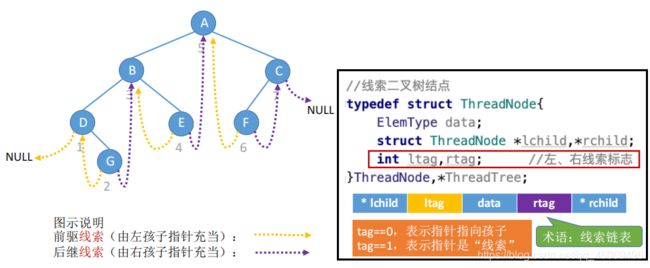
1. 定义
- 若无左子树，令lchild指向其前驱结点；若无右子树，令rchild指向其后继结点（n个结点的二叉树会有n+1个空指针）。还需增加两个标志域标识指针域是指向左（右）孩子还是前驱（后继）
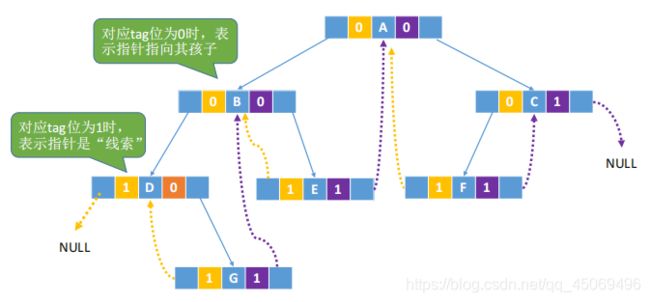
2. 存储结构
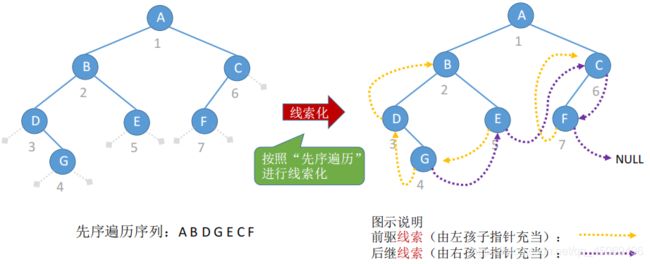
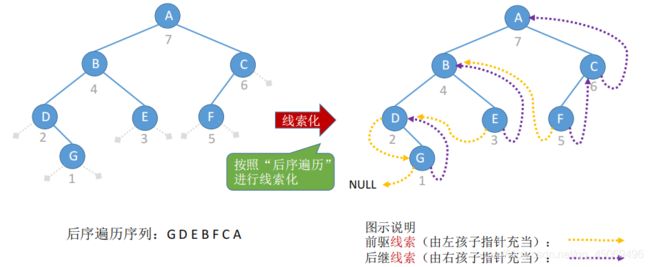
3. 线索化过程（手工模拟）
- 先序线索二叉树
- 先序线索化：将二叉树按先序遍历序列进行线索化（添加前驱和后继）
- 存储
- 先序线索化：将二叉树按先序遍历序列进行线索化（添加前驱和后继）
- 中序线索二叉树
-
中序线索化：将二叉树按中序遍历序列进行线索化（添加前驱和后继）
-
存储
-
- 后序线索二叉树
- 后序线索化：将二叉树按后序遍历序列进行线索化（添加前驱和后继）
- 存储
- 后序线索化：将二叉树按后序遍历序列进行线索化（添加前驱和后继）
4. 算法实现（了解即可）
- 结构体定义
typedef struct TBTNode { char data; int ltag, rtag; struct TBTNode *lchild; struct TBTNode *rchild; }TBTNode;
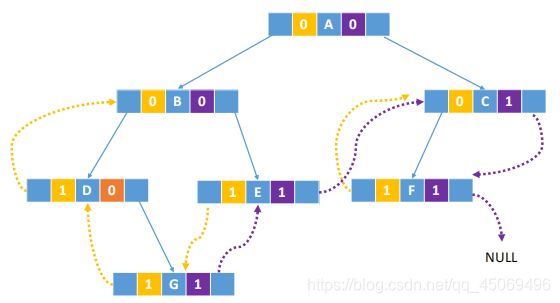
1. 中序线索二叉树（重点）
- 构造
//通过中序遍历对二叉树线索化的递归算法 void InThread(TBTNode *p, TBTNode *&pre) { if(p != NULL) { InThread(p->lchild, pre); //递归，左子树线索化 if(p->lchild == NULL) { //建立当前结点的前驱线索 p->lchild = pre; p->ltag = 1; } if(pre != NULL && pre->rchild == NULL) { //建立前驱结点的后继线索 pre->rchild = p; pre-rag = 1; } pre = p; InThread(p->rchild, pre); //递归，右子树线索化 } } //建立中序线索二叉树 void createInThread(TBTNode *root) { TBTNode *pre = NULL; if(root != NULL) { InThread(root, pre); pre->rchild = NULL; pre->rtag = 1; } } - 遍历
//求以p为根的中序线索二叉树中，中序序列下的第一个结点 TBTNode *First(TBTNode *p) { while(p->ltag == 0) p = p->lchild; //最左下结点（不一定是叶子结点） return p; } //求结点p在中序下的后继结点 TBTNode *Next(TBTNode *p) { if(p->rtag == 0) return First(p->rchild); else return p->rchild; //rtag == 1，直接返回线索 } //遍历 void InOrder(TBTNode *root) { for(TBTNode *p = First(root); p != NULL; p = Next(p)) visit(p); }
2. 前序线索二叉树
- 线索化
//通过前序遍历对二叉树线索化的递归算法 void PreThread(TBTNode *p, TBTNode *&pre) { if(p != NULL) { if(p->lchild == NULL) { //建立当前结点的前驱线索 p->lchild = pre; p->ltag = 1; } if(pre != NULL && pre->rchild == NULL) { //建立前驱结点的后继线索 pre->rchild = p; pre-rag = 1; } pre = p; if(p->ltag == 0) //左右指针不是线索才继续递归 PreThread(p->lchild, pre); if(p->rtag == 0) PreThread(p->rchild, pre); } } - 构造及遍历
//建立前序线索二叉树并遍历 void PreOrder(TBTNode *root) { if(root != NULL) { TBTNode *p = root; while(p != NULL) { while(p->ltage == 0)//左指针不是线索，则边访问边左移 { visit(p); p = p->lchild; } } visit(p); //此时p左指针比为线索，但还没有被访问 p = p->rchild; //此时p左孩子不存在，则右指针若非空，则不论是否为线索都指向其后继 } }
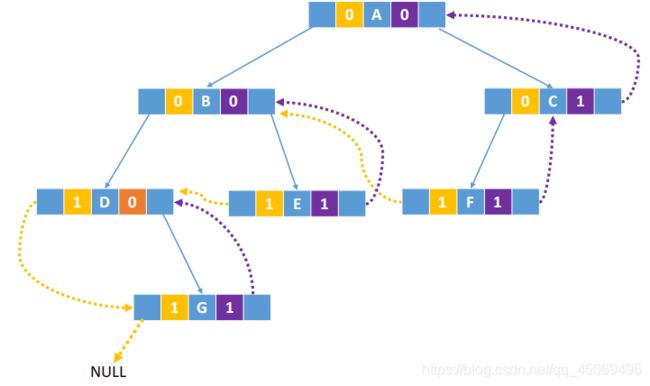
3. 后序线索二叉树
- 线索化
//通过后序遍历对二叉树线索化的递归算法 void PostThread(TBTNode *p, TBTNode *&pre) { if(p != NULL) { PostThread(p->lchild, pre); PostThread(p->rchild, pre); if(p->lchild == NULL) { //建立当前结点的前驱线索 p->lchild = pre; p->ltag = 1; } if(pre != NULL && pre->rchild == NULL) { //建立前驱结点的后继线索 pre->rchild = p; pre-rag = 1; } pre = p; } } - 找后继
- 若结点x是二叉树的根，则其后继为空
- 若结点x是其双亲的右孩子，或是其双亲的左孩子且其双亲没有右子树，则其后继即为双亲结点
- 若结点x是其双亲的左孩子，且其双亲有右子树，则其后继为双亲右子树上按后序遍历出的第一个结点
3. 算法应用
- 程序模板
void trave(BTNode *p) { if(p != NULL) { //(1) //若为先序遍历相关操作，则在该处添加相应代码 trave(p->lchild); //(2) //若为中序遍历相关操作，则在该处添加相应代码 trave(p->rchild); //(3) //若为后序遍历相关操作，则在该处添加相应代码 } }
1. 表达式(a-(b+c)*(d/e)存储在一颗以二叉链表为存储结构的二叉树中（二叉树结点的data域为字符型），编写程序求表达式的值（表达式的操作数都是一位数的整数）
- 算法思想：先遍历左子树求得左子树值，再遍历右子树得右子树值，最后访问根结点。因此采用后序遍历。
- 算法实现
int op(int a, int b, char ch) { if(ch == '+') return a+b; if(ch == '-') return a-b; if(ch == '*') return a*b; if(ch == '/') { if(b == 0) return 0; else return a/b; } } int comp(BTNode *p) { int A, B; if(p != NULL) { if(p->lchild != NULL && p->rchild != NULL) //如果当前结点的左右子树都非空，则为表达式 { A = comp(p->lchild); B = comp(p->rchild); return op(A, B, p->data); } else return p->data-'0'; } else return 0; }
2. 写一个算法求一棵二叉树的深度，二叉树以二叉链表为存储方式
- 算法思想：先求左子树深度，再求右子树深度，然后返回两者之中的最大值加1就是这棵树的深度
- 算法实现
- 递归实现
int getDepth(BTNode *p) { int LD, RD; if(p == NULL) return 0; //如果是空树，返回0 else { LD = getDepth(p->lchild); //求左子树深度 RD = getDepth(p->rchild); //求右子树深度 return (LD > RD ? LD : RD)+1; //即求整棵树的深度 } } - 非递归实现
int getDepth(BTNode *p) { if(!p) return 0; int front = -1, rear = -1; int last = 0, level = 0; //last指向当前层的最右结点 BTNode *Q[maxSize]; //设置队列Q，元素是二叉树结点指针且容量足够 Q[++rear] = p; BTNode *q; while(front < rear) { q = Q[++front]; //队列元素出队，即正在访问的结点 if(p->lchild) Q[++rear] = p->lchild; if(p->rchild) Q[++rear] = p->rchild; if(front == last) //某层元素遍历结束 { ++level; //层数加1 last = rear; } } return level; }
- 递归实现
3. 在一棵以二叉链表为存储结构的二叉树中，查找data域值等于key的结点是否存在（找到在任何一个满足要求的结点即可），如果存在，则将q指向该结点，否则q赋值为NULL，假设data为int型
- 算法思想：遍历整颗树，与将每个结点与key值对比
- 算法实现
void search(BTNode *p, BTNode *&q, int key) { if(p != NULL) //如果树为空，则什么都不做，q保持NULL值 { if(p->data == key) q = p; else { search(p->lchild, q, key); if(q == NULL) //左子树中没找到才到右子树中查找 search(p->rchild, q, key); } } }
4. 二叉树采用二叉链表存储结构存储，编写一个程序，输出先序遍历序列中第k个结点的值，假设k不大于总的结点数（结点data域为char型）
- 算法实现
int n = 0; //定义全局变量n，将结点计数初值设为0 void trave(BTNode *p, int k) { if(p != NULL) { ++n; //第一次来到一个结点就进行计数，表示这是第n个结点 if(k == n) //判断是不是第k个结点 { cout<<p->data<<endl; return; } trave(p->lchild, k); trave(p->rchild, k); } }
5. 假设二叉树采用二叉链表存储结构，设计一个算法，求出该二叉树具有结点数最多的那一层上结点个数
- 算法实现
typedef struct { BTNode *p; //结点指针 int lno; //结点所在层号 }St; int maxNode(BTNode *b) { St que [maxSize]; int front, rear; //定义非循环队列 int Lno = 0, i, j, n, max = 0; front = rear = 0; //将队列置空 BTNode *q; if(b != NULL) { ++rear; que[rear].p = b; //树根入队 que[rear].lno = 1; //树根所在层次号设为1 while(front != rear) { ++front; q = que[front].p; Lno = que[front].lno; //Lno用来存取当前结点的层次号 if(q->lchild != NULL) { ++rear; que[rear].p = q->lchild; que[rear].lno = Lno+1; //根据当前结点的层次号推知其孩子的层次号 } if(q->rchild != NULL) { ++rear; que[rear].p = q->rchild; que[rear].lno = Lno+1; } }//循环结束的时候，Lno中保存的是这棵二叉树的最大层数 max = 0; for(i = 1; i <= Lno; ++i) { n = 0; for(j = 0; j < rear; ++j) if(que[j].lno == i) ++n; if(max < n) max = n; } return max; } else return 0; }
6. 试给出二叉树的自下而上、从右到左的层次遍历方式
- 算法思想：利用原有的层次遍历算法，出队的同时将各结点指针入栈，在所有结点入栈后再从栈顶开始依次访问即为所求算法
- 算法实现
void invertLevel(BTNode *p) { int front, rear, top; BTNode *que[maxSize], *stack[maxSize]; //定义一个循环队列和一个栈 front=rear=0, top=-1; BTNode *q; if(p != NULL) { rear = (rear+1) % maxSize; que[rear] = p; while(front != rear) //队不空的时候循环 { front = (front+1) % maxSize; q = que[front]; stack[++top] = q; if(q->lchild != NULL) //若左子树不空，则左子树的根结点入栈 { rear = (rear+1) % maxSize; que[rear] = q->lchild; } if(q->rchild != NULL) //若右子树不空，则右子树的根结点入栈 { rear = (rear+1) % maxSize; que[rear] = q->rchild; } } while(top != -1) //依次访问栈中元素 visit(stack[top--]->data); } }
7. 设一棵二叉树中各结点的值互不相同，其先序遍历序列和中序遍历序列分别存于两个一维数组A[1···n]和B[1···n]中，试编写算法建立该二叉树的二叉链表
- 算法思想：根据先序序列确定树的根结点，根据根结点在中序序列中划分出二叉树的左右子树，然后根据左右子树结点在先序序列中的次序确定子树的根结点，直到每棵子树仅有一个结点为止
- 算法实现
BTNode *preInCreate(ElemType A[], ElemType B[], int LA, int RA, int LB, int RB) { root = (BTNode *)malloc(sizeof(BTNode)); //创建根结点 root->data = A[LA]; for(i = LB; B[i] != root->data; ++i); //根结点在中序序列的位置 Llen = i-LB; //左子树长度 Rlen = RB-i; //右子树长度 if(Llen) root->lchild = preInCreate(A, B, LA+1, LA+Llen, LB, LB+Llen-1); else root->lchild = NULL; if(Rlen) root->rchild = preInCreate(A, B, RA-Rlen+1, LA, RB-Rlen+1, RB); else root->rchild = NULL; return root; }
8. 二叉树按二叉链表形式存储，判别给定二叉树是否是完全二叉树
- 算法思想：采用层次遍历，将所有节点加入队列（包括空结点）。遇到空结点时，查看其后是否有非空结点。若有，则二叉树不是完全二叉树
- 算法实现
bool IsComplete(BTNode *T) { int front=0, rear=0; if(!T) //空树为满二叉树 return true; BTNode *queue[maxSize]; //定义一个队列，且其空间足够长（或定义循环队列） queue[++rear] = T; BTNode *p; while(front != rear) //遍历整棵树 { p = queue[++front]; if(p) { queue[++rear] = p->lchild; queue[++rear] = p->rchild; //若左右子树为空，则空结点入队 } else //队列先进先出的特点，空结点出队 while(front != rear) //若后面有非空结点，则返回false { p = queue[++front]; if(p) return false; } } return true; }
9. 二叉树采用二叉链表存储，计算一棵给定二叉树的所有双分支结点个数
- 算法实现
int DsonNodes(BTNode *b) { if(b == NULL) return 0; else if(b->lchild != NULL && b->rchild != NULL) return DsonNodes(b->lchild) + DsonNodes(b->rchild) + 1; else return DsonNodes(b->lchild) + DsonNodes(b->rchild); }
10. 二叉树B采用链式存储，编写一个算法交换B中所有结点的左、右子树
- 算法实现
void swap(BTNode *b) { if(b) { swap(b->lchild); swap(b->rchild); temp = b->lchild; b->lchild = b->rchild; b->rchild = temp; } }
11. 二叉树采用二叉链表存储，求先序遍历序列中第k（1 ≤ \le ≤k ≤ \le ≤二叉树中结点个数）个结点的值
- 算法实现
int i = 1; //遍历序号的全局变量 ElemType PreNode(BTNode *b, int k) { if(b == NULL) return '#'; //空结点，则返回特殊字符 if(i == k) //相等，则当前结点即为第k个结点 return b->data; i++; ch = PreNode(b->lchild, k); //左子树中递归寻找 if(ch != '#') return ch; ch = PreNode(b->rchild, k); //右子树中递归查找 return ch; }
12. 二叉树采用二叉链表存储，编写算法，删去树中每个以元素值为x的结点为根的子树，并释放相应的空间
- 算法思想：删除值为x的结点，意味着应将其父结点的左（右）子女指针置空，用层次遍历易于找到某结点的父结点
- 算法实现
void DeleteXTree(BTNode *bt) //删除以bt为根的子树 { if(bt) { DeleteXTree(bt->lchild); //删除bt的左右子树 DeleteXTree(bt->rchild); free(bt); } } void Search(BTNode *bt, ElemType x) //在二叉树上查找所有以x为元素值的结点，并删除以其为根的子树 { int front = rear = 0; BTNode *p; BTNode *Q[maxSize]; //Q是存放二叉树结点指针的队列，容量足够大 if(bt) { if(bt->data == x) //若根结点值为x，则删除整棵树 { DeleteXTree(bt); exit(0); } Q[++rear] = bt; while( front != rear) { p = Q[++front]; if(p->lchild) //若左子女非空 if(p->lchild->data == x) //左子树值等于x则删除左子树 { DeleteXTree(p->lchild); p->lchild = NULL; //左子女置空 } else Q[++rear] = p->lchild; if(p->rchild) //若右子女非空 if(p->rchild->data == x) //右子树值等于x则删除右子树 { DeleteXTree(p->rchild); p->rchild = NULL; //右子女置空 } else Q[++rear] = p->rchild; } } }
13. 二叉树中查找值为x的结点，打印值为x的结点的所有祖先，假设值为x的结点不多于一个
- 算法实现
typedef struct { BTNode *t; int tag; //tag=0表示左子女被访问，为1表示右子女被访问 }stack; void Search(BTNode *bt, ElemType x) { stack s[maxSize]; //栈容量足够大 int top = 0; while(bt != NULL || top > 0) { while(bt != NULL && bt->data != x) //结点入栈 { s[++top].t = bt; s[top].tag = 0; bt = bt->lchild; //沿左分支向下 } if(bt->data == x) { printg("所查结点的所有祖先结点的值为：\n"); for(int i =1; i <= top; i++); printf("%d", t->data); //输出祖先值后结束 exit(1); } while(top != 0 && s[top].tag == 1) --top; //退栈（空遍历） if(top != 0) { s[top].tag = 1; bt = s[top].t->rchild; //沿右分支向下遍历 } } }
14. 设一棵二叉树的结点结构为{LLINK, INFO, RLINK}，ROOT为指向该二叉树根结点的指针，p和q分别为指向该二叉树中任意两个结点的指针，编写算法ANCESTOR{ROOT, p, q, r}，找到p和q最近的公共祖先结点r
- 算法思想：采用后序非递归算法，栈中存放二叉树结点的指针，当访问到某结点时，栈中所有元素均为该结点的祖先。先将栈复制到另一辅助栈中，继续遍历到结点q时，将栈中元素从栈顶开始逐个到辅助栈中去匹配，第一个匹配的元素就是q和p的最近公共祖先
- 算法实现
typedef struct { BTNode *t; int tag; //tag=0表示左子女已被访问，tag=1表示右子女已被访问 }stack; stack s[maxSize], s1[maxSize]; //容量足够大 BTNode *Ancestor(BTNode *root, BTNode *p, BTNode *q) { int top = 0; BTNode *bt = root; while(bt != NULL || top > 0) { while(bt != NULL && bt != p && bt != q) //结点入栈 { while(bt != NULL) { s[++top].t = bt; s[top].tag = 0; bt = bt->lchild; //沿左分支向下 } } while(top != 0 && s[top].tag == 1) //假设p在q的左侧，遇到p时，栈中元素均为p的祖先 { if(s[top].t == p) { for(int = 1; i <= top; i++) //将栈s的元素转入辅助栈s1保存 s1[i] = s[i]; top1 = top; } if(s[top].t == q) //找到q结点 { for(i = top; i > 0; i--) //将栈中元素的树结点到s1中去匹配 for(int j = top1; j > 0; j--) if(s1[j].t == s[i].t) return s[i].t; //p和q的最近公共祖先已找到 --top; //退栈 } } if(top != 0) { s[top].tag = 1; bt = s[top].t->rchild; //沿右分支向下遍历 } }//while return NULL; //p和q无公共祖先 }
15. 设有一棵满二叉树（所有结点值均不同），已知其先序序列为pre，设计一个算法求其后序序列post
- 算法实现
void PreToPost(ElemType pre[], int l1, int h1, ElemType post[], int l2, int h2) { int half; if(h1 >= l1) { post[h2] = pre[h1]; half = (h1-l1)/2; PreToPost(pre ,l1+1, l1+half, post, l2, l2+half-1); //转换左子树 PreToPost(pre ,l1+half+1, h1, post, l2+half, h2-1); //转换右子树 } }
16. 设计一个算法将二叉树的叶结点按从左到右的顺序连成一个单链表，表头指针为head。二叉树按二叉链表方式存储，链接时用叶结点的右指针域来存放单链表指针
- 算法思想
- 算法实现
LNode *head, *pre = NULL; LNode *InOrder(BTNode *bt) { if(bt) { InOrder(bt->lchild); //中序遍历左子树 if(bt->lchild == NULL && bt->rchild == NULL) //叶结点 if(pre == NULL) //处理第一个叶结点 { head = bt; pre = bt; } else { pre->rchild = bt; pre = bt; } InOrder(bt->rchild); //中序遍历右子树 pre->rchild = NULL; //设置链表尾 } return head; }
17. 试设计判断两棵二叉树是否相似的算法。所谓二叉树T1和T2相似，指的是T1和T2都是空的二叉树或只有一个根结点；或T1的左子树和T2的左子树是相似的，且T1的右子树和T2的右子树是相似的
- 算法实现
int similar(BTNode *T1, BTNode *T2) { int leftS, rightS; if(T1 == NULL && T2 == NULL) return 1; else if(T1 == NULL || T2 == NULL) return 0; else { leftS = similar(T1->lchild, T2->lchild); rightS = similar(T1->rchild, T2->rchild); return leftS && rightS; } }
18. 写出在中序线索二叉树里查找指定结点在后序的前驱结点的算法
- 算法实现
TBTNode * InPostPre(TBTNode *t, TBTNode *p) { TBTNode *q; if(p->rtag == 0) //若p有右子女，则右子女时其后序前驱 q = p->rchild; else if(p->ltag == 0) //若p只有左子女，则左子女时其后序前驱 q = p->lchild; else if(p->lchild == NULL) q = NULL; //p是中序序列第一结点，无后序前驱 else //顺左线索向上找p的祖先，若存在，再找祖先的左子女 { while(p->ltag == 1 && p->lchild != NULL) p = p->lchild; if(p->ltag == 0) q = p->lchild; //p结点的祖先的左子女是其后序前驱 else q = NULL; //仅有单支树（p是叶子），已到根结点，p无后序前驱 } return q; }
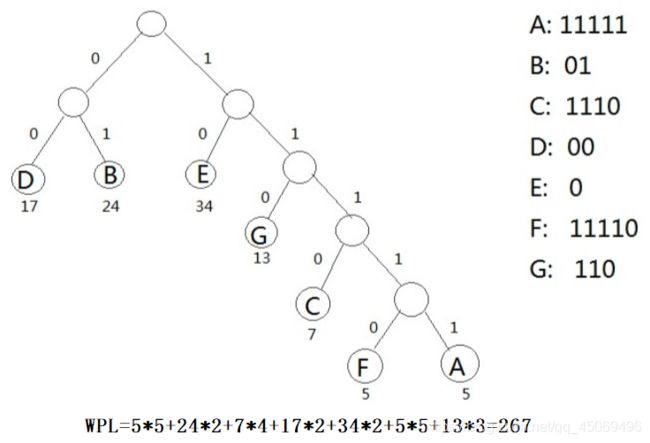
19. 二叉树的带权路径长度是二叉树中所有叶结点的带权路径长度之和。给定一棵二叉树T，采用二叉链表存储，结点结构为[left, weight, right]，其中叶结点的weight域保存该结点的非负权值。设root为指向T的根结点的指针，设计算法求T的WPL
- 算法思想
- 算法实现
typedef struct BTNode { int weight; struct BTNode *lchild, *rchild; }BTNode; //基于先序遍历的算法 int WPL(BTNode *root) { return wpl_PreOrder(root, 0); } int wpl_PreOrder(BTNode *root, int deep) { static int wpl = 0; //静态变量只初始化一次，以后每次调用仅改变其值 if(root->lchild == NULL && root->rchild == NULL)//若为叶结点，则累积wpl wpl += deep*root->weight; if(root->lchild != NULL) //若左子树不空，则递归遍历左子树 wpl_PreOrder(root->lchild, deep+1); if(root->rchild != NULL) //若右子树不空，则递归遍历右子树 wpl_PreOrder(root->rchild, deep+1); return wpl; } //基于层次遍历的算法 #define maxSize 100 //设置队列的最大容量 int wpl_LevelOrder(BTNode *root) { BTNode *q[maxSize]; //定义队列 int end1, end2; //end1队头指针，end2队尾指针 end1 = end2 = 0; //头指针指向队头元素，尾指针指向队尾的后一个元素 int wpl = 0, deep = 0; BTNode *lastNode; //lastNode用来记录当前层的最后一个结点 BTNode *newlastNode; //newlastNode用来记录下一层的最后一个结点 lastNode = root; //lastNode初始化为根结点 newlastNode = NULL; //newlastNode初始化为空 q[end2++] = root; //根结点入队 while(end1 != end2) //层次遍历，若队列不空则循环 { BTNode *t = q[end1++]; //拿出队列中的一个头元素 if(t->lchild == NULL && r->rchild == NULL) //若为叶结点，统计wpl wpl += deep*t->weight; if(t->lchild != NULL) //若非叶结点，把左结点入队 { q[end2++] = t->lchild; newlastNode = t->lchild; //设下一层的最后一个结点为该结点的左结点 } if(t->rchild != NULL) //处理叶结点 { q[end2++] = t->rchild; newlastNode = t->rchild; } if(t == lastNode) //若该结点为本层最后一个结点，则更新lastNode { lastNode = newlastNode; deep += 1; //层数加1 } } return wpl; }
20. 设计一个算法，将给定的表达式树（二叉树）转换为等价的中缀表达式（通过括号反应操作符的计算次序）并输出
- 算法思想
- 算法实现
typedef struct node { char data[10]; //存储操作数或操作符 struct node *left, *right; }BTree; void BTreeToE(BTNode *root) { BTreeToE(root, 1); //根的高度为1 } void BTreeToExp(BTNode *root, int deep) { if(root == NULL) return; //空结点返回 else if(root->left == NULL && root->right == NULL) printf("%s", root->data); //输出操作数，不加括号 else { if(deep > 1) printf("("); //若有子表达式则加1层括号 BTreeToExp(root->left, deep+1); printf("%s", root->data); //输出操作符 BTreeToExp(root->right, deep+1); if(deep > 1) printf(")"); //若有右表达式则加1层括号 } }
4. 树、森林
1. 树的存储结构
- 双亲表示法：采用一组连续空间来存储每个结点，同时在每个结点中增设一个伪指针，指示其双亲结点在数组中的位置
- 孩子表示法：将每个结点的孩子结点都用单链表链接起来形成一个线性结构，此时n个结点就有n个孩子链表（叶子结点的孩子链表为空表）
- 孩子兄弟表示法：左指针指向孩子结点，右指针指向兄弟结点
2. 树、森林与二叉树的转换
- 规则：每个结点左指针指向它的第一个孩子，右指针指向它在树中相邻的右兄弟（左孩子右兄弟）
3. 树和森林的遍历
1. 树的遍历
- 先根遍历：先访问根结点，再依次遍历根结点的每棵子树（等价于这棵树转化为二叉树的先序序列）
- 后根遍历：先依次遍历根结点的每棵子树，再访问根结点（等价于这棵树转化为二叉树的中序序列）
2. 森林的遍历
- 先序遍历森林：对每棵树依次进行先根遍历（等价于这个森林转化为二叉树的先序序列）
- 中（后）序遍历森林：对每棵树依次进行后根遍历（等价于这个森林转化为二叉树的中序序列）
3. 哈夫曼树与哈夫曼编码
- 相关概念
- 路径：从树中一个结点到另一个结点的分支所构成的路线
- 路径长度：路径上边的个数
- 树的路径长度：根到各个结点的路径长度之和
- 带权路径长度：从该结点到根之间的路径长度乘以结点的权值，就是该结点的带权路径长度
- 树的带权路径长度（WPL）：树中所有叶子结点的带权路径长度之和
- 哈夫曼树的构造
- 将n个结点分别作为n棵仅含一个结点的二叉树，构成森林F
- 构造一个新结点，从F中选取两棵根结点权值最小的树作为新结点的左右子树，并且将新结点的权值置为左右子树上根结点的权值之和
- 从F中删除刚才选出的两棵子树，同时将新得到的树加入F中
- 重复2、3两步，直到F中只剩下一棵树为止
- 哈夫曼树的特点
- 每个初始结点都是叶结点，且权值越小的结点到根结点的路径长度越大
- 结点总数为2n-1（终端结点n-1个）
- 不存在度为1的结点
- 不唯一，但各哈夫曼树的带权路径长度相同且最优
- 哈夫曼编码
- 前缀编码：没有一个编码是另一个编码的前缀
- 每条边由一位二进制位表示，左0右1，从根结点到叶子结点的路径的各条边依次用0、1表示即为该叶子结点的哈夫曼编码
4. 算法应用
1. 求以孩子兄弟表示法存储的森林的叶子结点数
- 算法实现
typedef struct BTNode { ElemType data; struct BTNode *fch, *nsib; //孩子域与兄弟域 }BTNode; int Leaves(BTNode *bt) { if(bt == NULL) //树空返回0 return 0; if(t->fch == NULL) //若结点无孩子，则该结点必是叶子 return 1+Leaves(bt->nsib); //返回叶子结点和其兄弟子树中的叶子结点数 else return Leaves(bt->fch) + Leaves(bt->nsib); //返回孩子子树和兄弟子树中叶子数之和 }
2. 以孩子兄弟链表为存储结构，涉及递归算法求树的深度
- 算法实现
int Height(BTNode *bt) { int hc, hs; if(bt == NULL) return 0; else { hc = Height(bt->fch); hs = Height(bt->nsib); if(hc+1 > hs) reutrn hc+1; else return hs; } }
3. 已知一棵树的层次序列及每个结点的度，编写算法构造此树的孩子兄弟链表
- 算法思想
- 算法实现
#define maxNode 15 void createGSTree_Degree(BTNode *&T, DateType e[], int degree[], int n) { BTNode *pointer = new BTNode[maxNodes]; int i, j, d, k=0; for(i = 0; i < n; ++i) { pointer[i]->data = e[i]; pointer[i]->lchild = pointer[i]->rchild = NULL; } for(i = 0; i < n; ++i) { d = degree[i]; //结点i的度数 if(d) { ++k; //k为子女结点序号 pointer[i]->lchild = pointer[k]; //建立i与子女k间的链接 for(j = 2; j <= d; ++j) pointer[(++k)-1]->rchild = pointer[k]; } } T = pointer[0]; delete[] pointer; //释放数组 }
5. 树与二叉树的应用
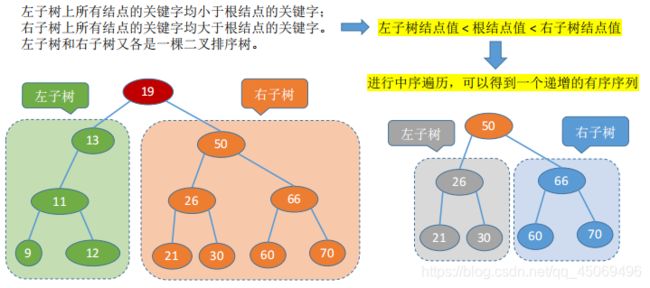
1. 二叉排序树（BST）
1. 定义(左 < 根 < 右)
2. 基本操作
- 查找
BSTNode *BST_Search(BTNode *T, ElemType key) { while(T != NULL && key != T->data) { if(key < T->data) T = T->lchild; else T = T->rchild; } return T; } - 插入
int BST_Insert(BTNode *&T, KeyType k) { if(T == NULL) //原树为空，新插入的记录为根结点 { T = (BTNode *)malloc(sizeof(BTNode)); T->key = k; T->lchild = T->rchild = NULL; return 1; //返回1，插入成功 } else if(k == T->key) //树中存在相同关键字的结点，插入失败 return 0; else if(k < T->key) //插入到T的左子树 return BST_Insert(T->lchild, k); else //插入到T的右子树 return BST_Insert(T->rchild, k); } - 构造
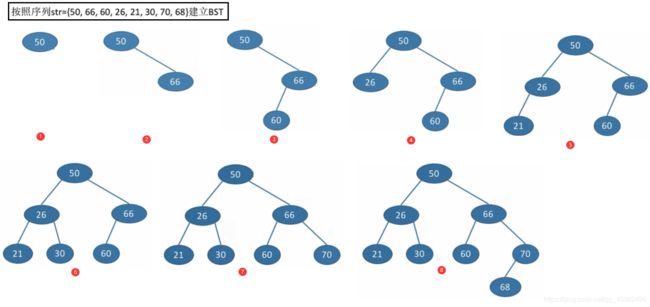
void Create_BST(BTNode *&T, KeyType str[], int n) { T = NULL; //初始时T为空树 int i = 0; while(i < n) //依次将每个关键字插入到二叉排序树中 { BST_Insert(T, str[i]); i++; } } - 删除
- 流程
- 若被删除结点z为叶结点，则让z的子树成为z父结点的子树，代替z的位置
- 若结点z只有一棵左子树或右子树，则让z的子树成为z父结点的子树，代替z的位置
- 若结点z有左、右两棵子树，则令z的直接后继（或直接前驱）替代z，然后从二叉排序树中删去这个直接后继（或直接前驱），这样就转换成了第一或第二种情况
- 注意
- 若先删除叶结点再插入该结点，则得到的二叉排序树和原来相同
- 若先删除非叶结点再插入该结点，则得到的二叉排序树和原来不同
- 流程
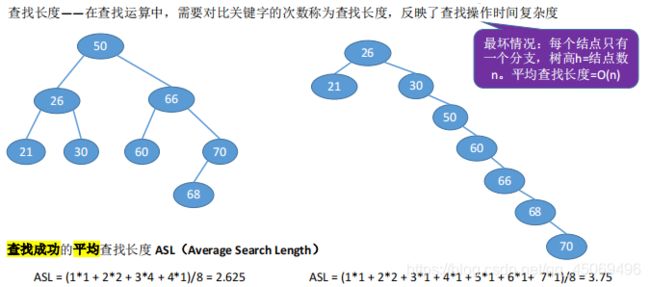
3. 查找效率分析
主要取决于树的高度
- 最坏情况
- 只有一个孩子的单支树：O(n)
- 最好情况
- 平衡二叉树：O( log 2 n \log_2 n log2n)
- 等概率情况
-
查找成功
-
查找失败
-
2. 平衡二叉树（AVL）
1. 定义
- 在插入和删除二叉树结点时，要保证任意节点的左、右子树高度差的绝对值不超过1
- 左子树域右子树的高度差为该结点的平衡因子（只能是-1、0、1）
2. 基本操作
-
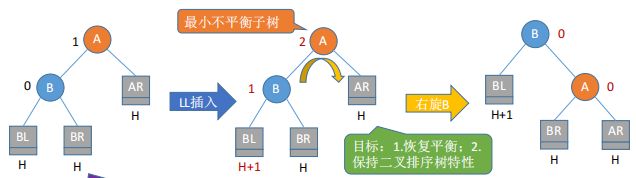
插入：首先检查其插入路径上的结点是否因为此次操作而导致了不平衡，若导致了不平衡，则先找到插入路径上离插入结点最近的平衡因子的绝对值大于1的结点A，再对以A为根的子树，在保持二叉排序树特性的前提下，调整各结点的位置关系，使之重新达到平衡
-
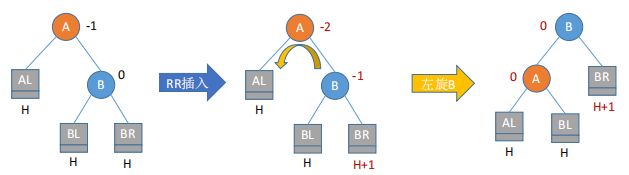
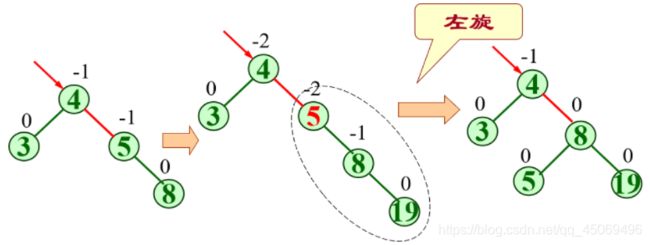
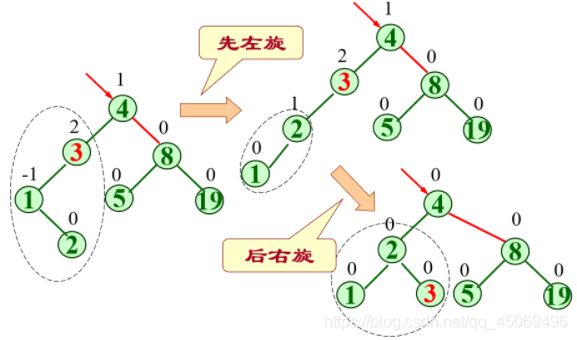
LL旋转：结点A的左孩子的左子树插入了新结点。
- A的左孩子B向右上旋转代替A成为根结点
- A向右下旋转成B的右子树的根结点
- B的原右子树作为A的左子树
-
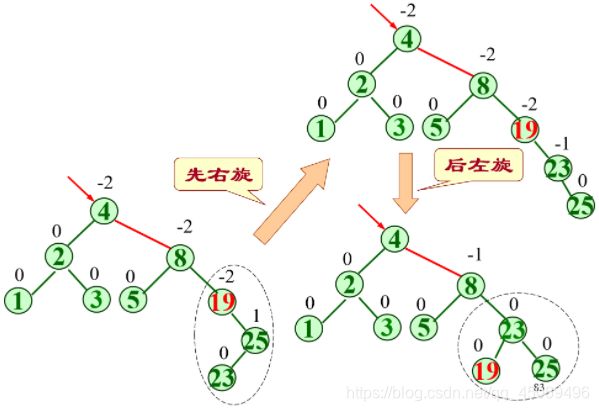
RR旋转：结点A的右孩子的右子树插入了新结点
- A的右孩子B向左上旋转代替A成为根结点
- A向左下旋转成为B的左子树的根结点
- B的原左子树则作为A的右子树
-
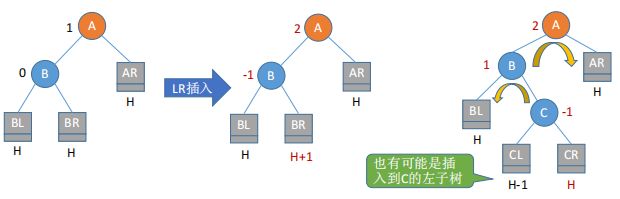
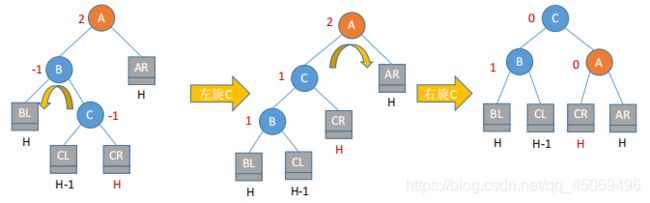
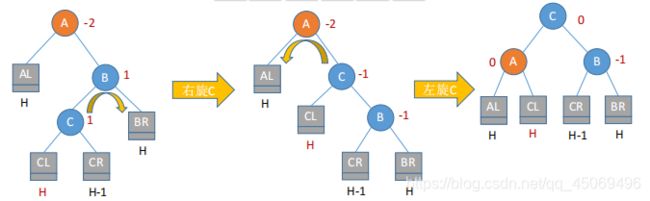
LR旋转：结点A的左孩子的右子树插入了新结点
- A的左孩子B的右子树的根结点C向左上旋转提升到B的位置
- C向右上旋转提升到A的位置
-
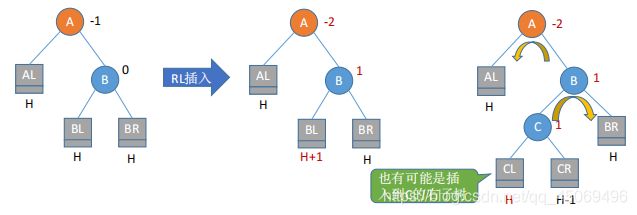
RL旋转：结点A的右孩子的左子树插入了新结点
- A的右孩子B的左子树的根结点C向右上旋转提升到B的位置
- C向左上旋转提升到A的位置
-
LR和RL旋转时，新结点究竟是插入C的左子树还是右子树不影响旋转过程
- 查找
- 与给定值比较的关键字个数不超过树的深度
- 含有n个结点的平衡二叉树的最大深度为O( log 2 n \log_2 n log2n)，平均查找长度为O( log 2 n \log_2 n log2n)
- 假设 n h n_h nh表示深度为h的平衡树中含有的最少结点数（求解给定结点数的平衡二叉树最多比较次数）
3. 并查集
- 思想：用集合中的一个元素代表一个集合
- 应用
- 求无向图的连通分量个数
- 最小公共祖先
- 实现Kruskar算法求最小生成树
- 判断有无环路
#define VERTICES 6
void initialise(int parent[], int rank[]){ //父结点数组、深度数组初始化
int i;
for(i = 0; i < VERETICES; i++){
parent[i] = -1;
rank[i] = 0;
}
}
int find_root(int x, int parent[]){ //找指定结点的根结点
int x_root = x;
while(parent[x_root] != -1)
x_root = parent[x_root];
return x_root;
}
/**
* 1---union successfully 俩结点不在同一集合时，合并
* 0---failed 否则不合并
*/
int union_vertices(int x, int y, int parent[], int rank[]){
int x_root = find_root(x, parent);
int y_root = find_root(y, parent);
if(x_root == y_root)
return 0;
else{
if(rank[x_root] > rank[y_root]){ //x根结点深度 > y根结点深度，y认x做老大
parent[y_root] = x_root;
}else if(rank[x_root] < rank[y_root]){ //x根结点深度 < y根结点深度，x认y做老大
parent[x_root] = y_root;
}else{ //x根结点深度 < y根结点深度，让x做老大，高度加1
rank[x_root]++;
parent[y_root] = x_root;
}
return 1;
}
}
int main(){
int parent[VERTICES] = {0};
int edges[6][2] = {
{0,1}, {1,2}, {1,3}，
{2,4}, {3,4}, {2,5}
};
initialise(parent);
int i;
for(i = 0; i < 6; i++){
int x = edges[i][0];
int y = edges[i][1];
if(union_vertices(x, y, parent) == 0){
printf("Cycle detected!"\n);
exit(0);
}
}
printf("No cycle found."\n);
}
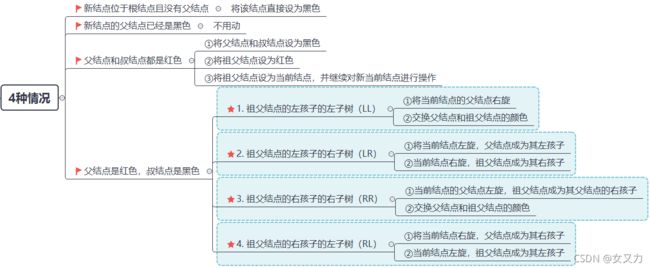
4. 红黑树
1. 性质和特点
- 五大性质
- 每个结点要么是红色要么是黑色
- 根结点为黑色
- 每个叶子结点是黑色的（叶子结点为空）
- 红色结点的子结点必为黑色结点（不能有两个连续的红结点）
- 从任意一个结点到其叶子的所有路径中，所包含的黑结点数量相同（没有一条路径会比其他路径长出两倍）
- 特点
- 插入删除最坏情况下时间复杂度为 O ( l o g 2 n ) O(log_2 n) O(log2n)
- 红黑树的高度最多为 2 l o g 2 ( n + 1 ) 2log_2(n+1) 2log2(n+1)
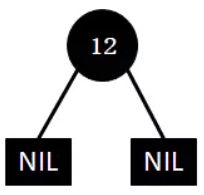
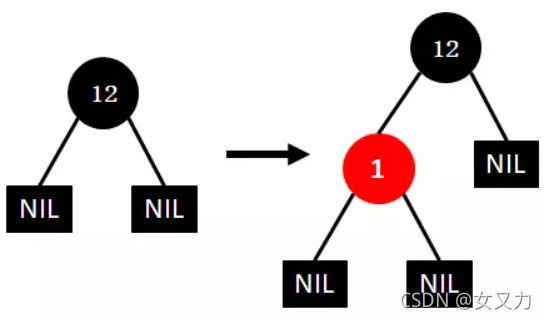
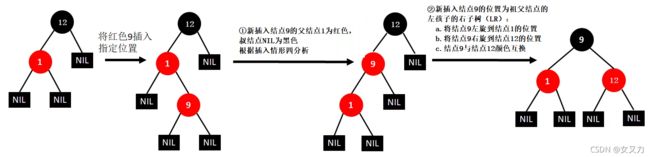
2. 插入规则
新插入结点默认为红色
①插入12
说明：插入的结点若是根结点，则直接置为黑色
②插入1
说明：插入结点默认为红色
③插入9
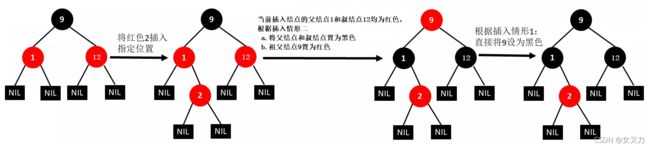
④插入2
⑤插入0
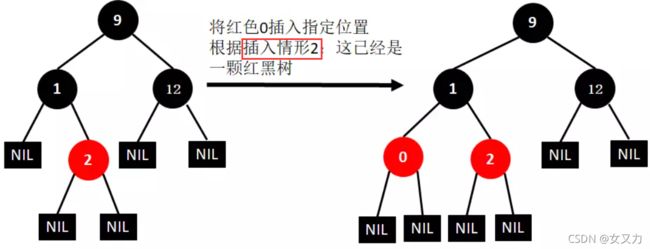
⑥插入11
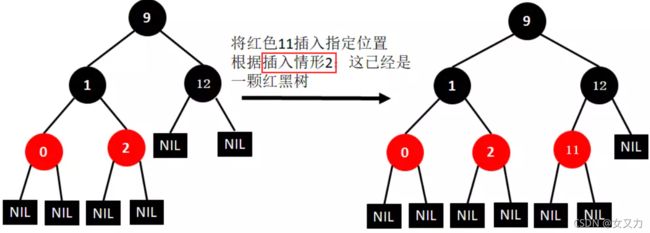
⑦插入7
⑧插入19
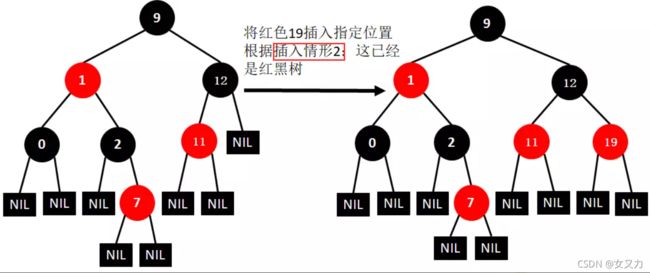
⑨插入4
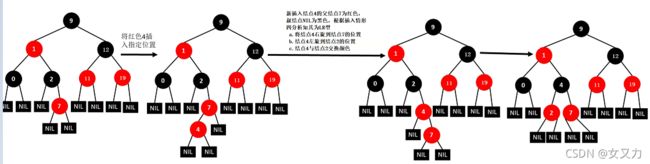
⑩插入15
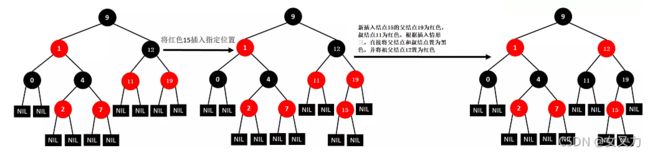
⑪插入18
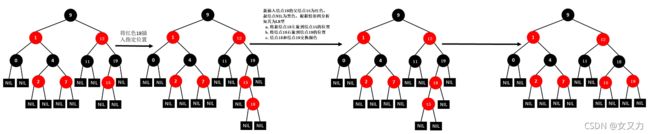
⑫插入5
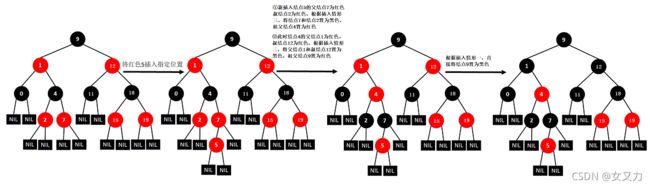
⑬插入14
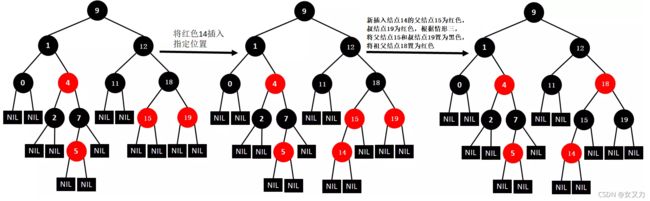
⑭插入13
⑮插入10
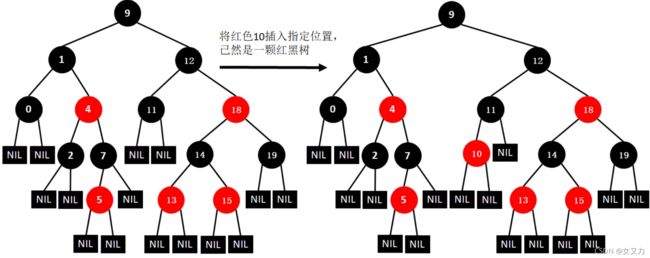
⑯插入16
⑰插入6
⑱插入3
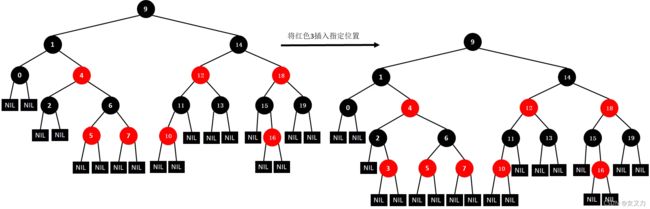
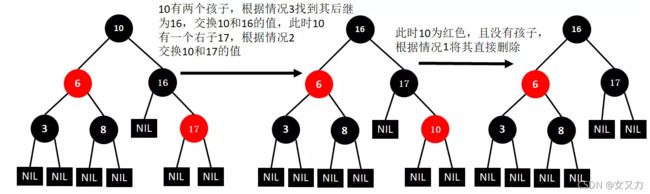
3. 删除规则
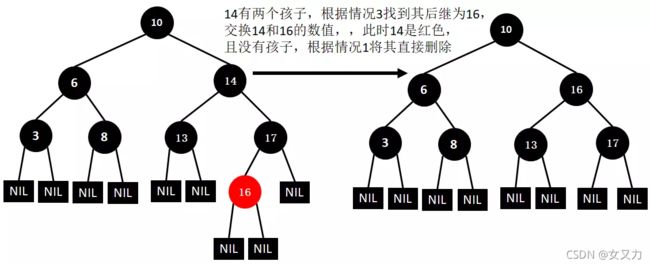
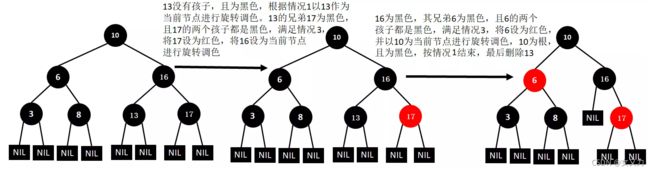
第一步：从树中删除结点X（以寻找后继结点的方式删除）
- 情况1：X没有孩子
- X为红色，直接删除
- X为黑色，以X为当前结点进行旋转调色
- 情况2：X有一个孩子C
- 交换X和C的数值，再对X进行删除
- 情况3：X有两个孩子
- 和后继中最小结点D交换数值，再对X进行删除
第二步：旋转调色
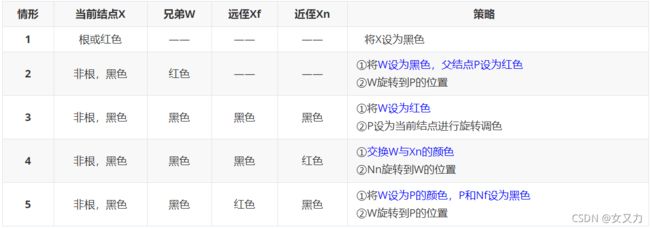
①删除12
②删除1
③删除9
④删除2
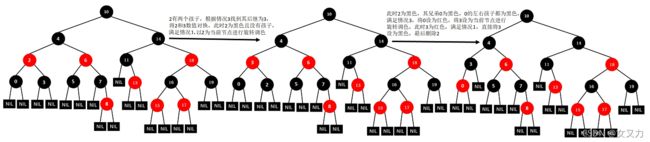
⑤删除0
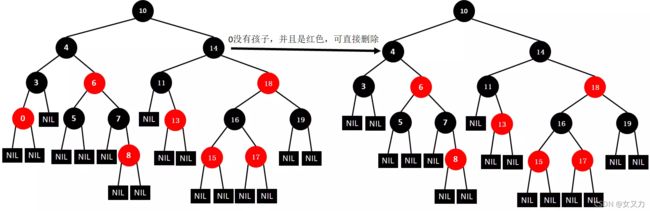
⑥删除11
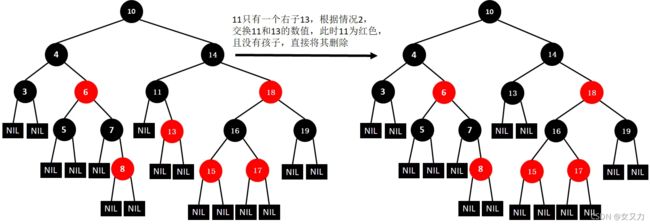
⑦删除7
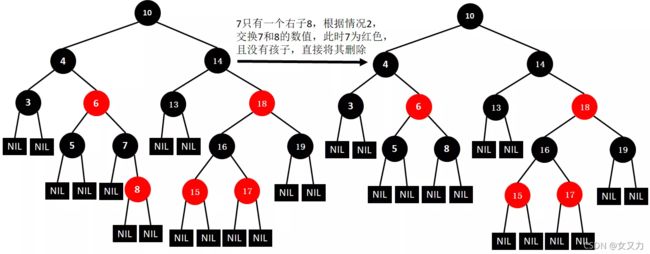
⑧删除19
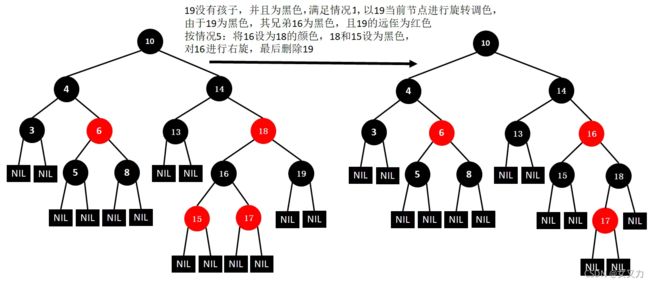
⑨删除4
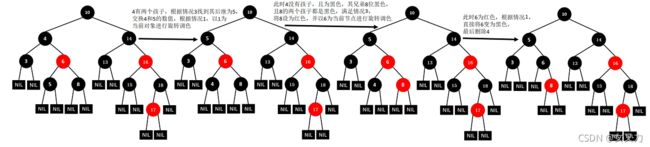
⑩删除15
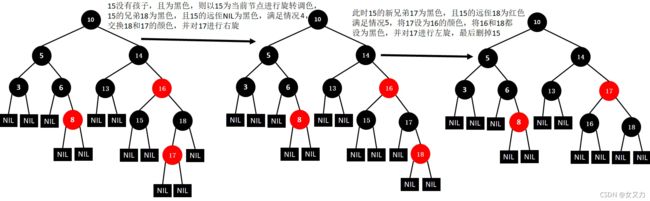
⑪删除18
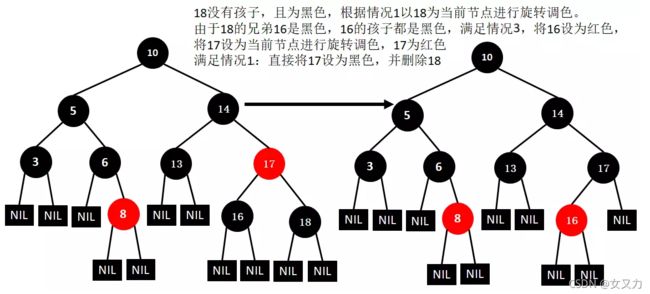
⑫删除5
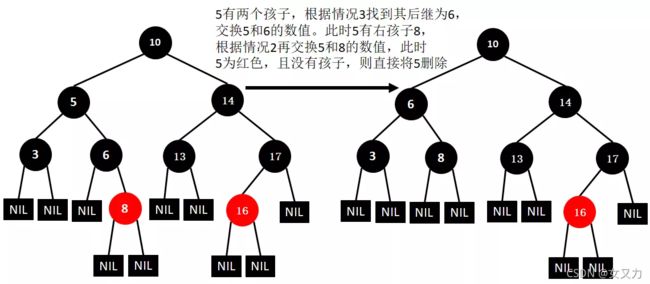
⑬删除14
⑭删除13
⑮删除10
