【数据结构】树及其应用

问题 A: DS树–二叉树高度

题目描述

给出一棵二叉树，求它的高度。二叉树的创建采用前面实验的方法。
注意，二叉树的层数是从1开始

输入

第一行输入一个整数t，表示有t个二叉树
第二行起输入每个二叉树的先序遍历结果，空树用字符‘0’表示，连续输入t行

输出

每行输出一个二叉树的高度

样例输入

1
AB0C00D00

样例输出

3

题解

#include
using namespace std;

typedef struct BTree_node {
	char data;
	struct BTree_node* LChild;
	struct BTree_node* RChild;
	int depth = 0;
}BTree;

class Btree {
public:
	BTree_node* root;
	int depth;
	int i;
	Btree() {
		root = NULL;
		depth = 0;
		i = 0;
	}
	void Create_BTree(BTree*& t)
	{
		char s;
		cin >> s;
		if (s == '0')
			t = NULL;
		else
		{
			t = new BTree_node;
			t->data = s;
			Create_BTree(t->LChild);
			Create_BTree(t->RChild);
		}
	}
	void cal_Depth(BTree* t,int i)
	{
		if (t)
		{
			i++;
			if (t->LChild == NULL && t->RChild == NULL)
			{
				if (depth < i)
					depth = i;
			}
			cal_Depth(t->LChild, i);
			cal_Depth(t->RChild, i);
		}
	}
};



int main() {
	int t;
	cin >> t;
	while (t--) {
		Btree tree;
		tree.Create_BTree(tree.root);
		tree.cal_Depth(tree.root, 0);
		cout << tree.depth << endl;
	}

	return 0;
}

---

问题 B: DS树–二叉树之最大路径

题目描述

给定一颗二叉树的逻辑结构（先序遍历的结果，空树用字符‘0’表示，例如AB0C00D00），建立该二叉树的二叉链式存储结构
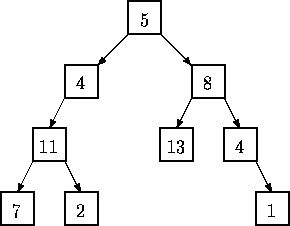
二叉树的每个结点都有一个权值，从根结点到每个叶子结点将形成一条路径，每条路径的权值等于路径上所有结点的权值和。编程求出二叉树的最大路径权值。如下图所示，共有4个叶子即有4条路径，
路径1权值=5 + 4 + 11 + 7 = 27
路径2权值=5 + 4 + 11 + 2 = 22
路径3权值=5 + 8 + 13 = 26
路径4权值=5 + 8 + 4 + 1 = 18
可计算出最大路径权值是27。
该树输入的先序遍历结果为ABCD00E000FG00H0I00，各结点权值为：
A-5，B-4，C-11，D-7，E-2，F-8，G-13，H-4，I-1

输入

第一行输入一个整数t，表示有t个测试数据
第二行输入一棵二叉树的先序遍历，每个结点用字母表示
第三行先输入n表示二叉树的结点数量，然后输入每个结点的权值，权值顺序与前面结点输入顺序对应
以此类推输入下一棵二叉树

输出

每行输出每棵二叉树的最大路径权值，如果最大路径权值有重复，只输出1个

样例输入

2
AB0C00D00
4 5 3 2 6
ABCD00E000FG00H0I00
9 5 4 11 7 2 8 13 4 1

样例输出

11
27

题解

#include
using namespace std;

typedef struct BTree_node {
	char data;
	struct BTree_node* LChild;
	struct BTree_node* RChild;
	int value;
}BTree;

class Btree {
public:
	BTree_node* root;
	int depth;
	int i;
	int MaxRoutine;
	Btree() {
		root = NULL;
		depth = 0;
		i = 0;
		MaxRoutine = 0;
	}
	void Create_BTree(BTree*& t)
	{
		char s;
		cin >> s;
		if (s == '0')
			t = NULL;
		else
		{
			t = new BTree_node;
			t->data = s;
			Create_BTree(t->LChild);
			Create_BTree(t->RChild);
		}
	}
	void cal_Depth(BTree* t, int i)
	{
		if (t)
		{
			i++;
			if (t->LChild == NULL && t->RChild == NULL)
			{
				if (depth < i)
					depth = i;
			}
			cal_Depth(t->LChild, i);
			cal_Depth(t->RChild, i);
		}
	}
	void set_value(BTree* t) {
		if (t) {
			cin >> t->value;
			set_value(t->LChild);
			set_value(t->RChild);
		}
	}
	void cal_MaxRoutine(BTree* t, int val) {
		if (t) {
			val += t->value;
			if (t->LChild == NULL && t->RChild == NULL) {
				if (val > MaxRoutine) {
					MaxRoutine = val;
				}
			}
			cal_MaxRoutine(t->LChild, val);
			cal_MaxRoutine(t->RChild, val);
		}
	}
};

int main() {
	int t;
	cin >> t;
	while (t--) {
		Btree tree;
		tree.Create_BTree(tree.root);
		int data;
		cin >> data;
		tree.set_value(tree.root);
		tree.cal_MaxRoutine(tree.root, 0);
		cout << tree.MaxRoutine << endl;
	}

	return 0;
}

---

问题 C: DS树–带权路径和

题目描述

计算一棵二叉树的带权路径总和，即求赫夫曼树的带权路径和。
已知一棵二叉树的叶子权值，该二叉树的带权案路径和APL等于叶子权值乘于根节点到叶子的分支数，然后求总和。如下图中，叶子都用大写字母表示，权值对应为：A-7，B-6，C-2，D-3
树的带权路径和 = 71 + 62 + 23 + 33 = 34
本题二叉树的创建参考前面的方法

输入

第一行输入一个整数t，表示有t个二叉树
第二行输入一棵二叉树的先序遍历结果，空树用字符‘0’表示，注意输入全是英文字母和0，其中大写字母表示叶子
第三行先输入n表示有n个叶子，接着输入n个数据表示n个叶子的权值，权值的顺序和前面输入的大写字母顺序对应
以此类推输入下一棵二叉树

输出

输出每一棵二叉树的带权路径和

样例输入

2
xA00tB00zC00D00
4 7 6 2 3
ab0C00D00
2 10 20

样例输出

34
40

题解

#include
using namespace std;

typedef struct BTree_node {
	char data;
	struct BTree_node* LChild;
	struct BTree_node* RChild;
	int value;
}BTree;

class Btree {
public:
	BTree_node* root;
	int depth;
	int i;
	int MaxRoutine;
	int value;
	Btree() {
		root = NULL;
		depth = 0;
		i = 0;
		MaxRoutine = 0;
		value = 0;
	}
	void Create_BTree(BTree*& t)
	{
		char s;
		cin >> s;
		if (s == '0')
			t = NULL;
		else
		{
			t = new BTree_node;
			t->data = s;
			Create_BTree(t->LChild);
			Create_BTree(t->RChild);
		}
	}
	void cal_Depth(BTree* t, int i)
	{
		if (t)
		{
			i++;
			if (t->LChild == NULL && t->RChild == NULL)
			{
				if (depth < i)
					depth = i;
			}
			cal_Depth(t->LChild, i);
			cal_Depth(t->RChild, i);
		}
	}
	void set_value(BTree* t) {
		if (t) {
			if (t->LChild == NULL && t->RChild == NULL)
				cin >> t->value;
			set_value(t->LChild);
			set_value(t->RChild);
		}
	}
	void cal_MaxRoutine(BTree* t, int val) {
		if (t) {
			val += t->value;
			if (t->LChild == NULL && t->RChild == NULL) {
				if (val > MaxRoutine) {
					MaxRoutine = val;
				}
			}
			cal_MaxRoutine(t->LChild, val);
			cal_MaxRoutine(t->RChild, val);
		}
	}
	void cal(BTree* t, int deep) {
		if (t) {
			if (t->LChild == NULL && t->RChild == NULL) {
				value += t->value * deep;
			}
			deep++;
			cal(t->LChild, deep);
			cal(t->RChild, deep);
		}
	}
};

int main() {
	int t;
	cin >> t;
	while (t--) {
		Btree tree;
		tree.Create_BTree(tree.root);
		int data;
		cin >> data;
		tree.set_value(tree.root);
		tree.cal(tree.root, 0);
		cout << tree.value << endl;		
	}

	return 0;
}

---

问题 D: DS二叉树–赫夫曼树的构建与编码（含代码框架）

题目描述

给定n个权值，根据这些权值构造huffman树，并进行huffman编码
参考课本算法，注意数组访问是从位置1开始
要求：赫夫曼的构建中，默认左孩子权值不大于右孩子权值
代码框架参考如下：

输入

第一行输入t，表示有t个测试实例
第二行先输入n，表示第1个实例有n个权值，接着输入n个权值，权值全是小于1万的正整数
依此类推

输出

逐行输出每个权值对应的编码，格式如下：权值-编码
即每行先输出1个权值，再输出一个短划线，再输出对应编码，接着下一行输入下一个权值和编码。
以此类推

样例输入

1
5 15 4 4 3 2

样例输出

15-1
4-010
4-011
3-001
2-000

题解

#include
#include
#include
using namespace std;

const int MaxW = 9999;
class HuffNode {
public:
	int weight;
	int parent;
	int leftchild;
	int rightchild;
};

class HuffMan {
private:
	void MakeTree();
	void SelectMin(int pos, int* s1, int* s2);
public:
	int len;
	int lnum;
	HuffNode* huffTree;
	string* huffCode;
	void MakeTree(int n, int wt[]);
	void Coding();
	void Destroy();
};

void HuffMan::MakeTree()
{
	int i, s1, s2;
	for (i = lnum + 1; i <= len; i++) {
		SelectMin(i - 1, &s1, &s2);
		huffTree[s1].parent = i;
		huffTree[s2].parent = i;
		huffTree[i].leftchild = s1;
		huffTree[i].rightchild = s2;
		huffTree[i].weight = huffTree[s1].weight + huffTree[s2].weight;
	}
}

void HuffMan::SelectMin(int pos, int* s1, int* s2)
{
	int w1, w2, i;
	w1 = w2 = MaxW;
	*s1 = *s2 = 0;
	for (i = 1; i <= pos; i++) {
		if (huffTree[i].weight < w1 && huffTree[i].parent == 0) {
			w2 = w1;
			*s2 = *s1;
			w1 = huffTree[i].weight;
			*s1 = i;
		}
		else if (huffTree[i].weight < w2 && huffTree[i].parent == 0) {
			w2 = huffTree[i].weight;
			*s2 = i;
		}
	}
}

void HuffMan::MakeTree(int n, int wt[])
{
	int i;
	lnum = n;
	len = 2 * n - 1;
	huffTree = new HuffNode[2 * n];
	huffCode = new string[lnum + 1];
	for (i = 1; i <= n; i++)
		huffTree[i].weight = wt[i - 1];
	for (i = 1; i <= len; i++) {
		if (i > n)
			huffTree[i].weight = 0;
		huffTree[i].parent = 0;
		huffTree[i].leftchild = 0;
		huffTree[i].rightchild = 0;
	}
	MakeTree();
}

void HuffMan::Coding()
{
	char* cd;
	int i, c, f, start;
	cd = new char[lnum];
	cd[lnum - 1] = '\0';
	for (i = 1; i <= lnum; ++i) {
		start = lnum - 1;
		for (c = i, f = huffTree[i].parent; f != 0; c = f, f = huffTree[f].parent) {
			if (huffTree[f].leftchild == c) {
				cd[--start] = '0';
			}
			else {
				cd[--start] = '1';
			}
		}
		huffCode[i].assign(&cd[start]);
	}
	delete[]cd;
}

void HuffMan::Destroy()
{
	len = 0;
	lnum = 0;
	delete[]huffTree;
	delete[]huffCode;
}

int main() {
	int t, n, i, j;
	int wt[800];
	HuffMan myhuff;
	cin >> t;
	for (i = 0; i < t; i++) {
		cin >> n;
		for (j = 0; j < n; j++)
			cin >> wt[j];
		myhuff.MakeTree(n, wt);
		myhuff.Coding();
		for (j = 1; j <= n; j++) {
			cout << myhuff.huffTree[j].weight << '-';
			cout << myhuff.huffCode[j] << endl;
		}
		myhuff.Destroy();
	}
	return 0;
}

---