深圳大学计软《数据结构》实验07--二叉树及其应用

问题 A: DS二叉树—二叉树构建与遍历（不含框架）

题目描述

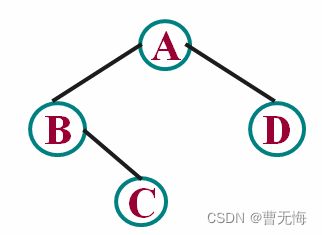
给定一颗二叉树的逻辑结构如下图，（先序遍历的结果，空树用字符‘#’表示，例如AB#C##D##），建立该二叉树的二叉链式存储结构，并输出该二叉树的先序遍历、中序遍历和后序遍历结果。

输入

第一行输入一个整数t，表示有t个二叉树

第二行起输入每个二叉树的先序遍历结果，空树用字符‘#’表示，连续输入t行。

输出

输出每个二叉树的先序遍历、中序遍历和后序遍历结果。

样例输入

2
AB#C##D##
AB##C##

样例输出

ABCD
BCAD
CBDA
ABC
BAC
BCA

AC代码

#include
using namespace std;

struct BTree_node
{
	char date;
	BTree_node* left, * right;
	void set(char c, BTree_node* l = NULL, BTree_node* r = NULL) { date = c; left = l; right = r; }
};

class BTree {
	BTree_node* root;
	void preorder_tra(BTree_node* node) {
		if (!node)
			return;
		cout << node->date;
		preorder_tra(node->left);
		preorder_tra(node->right);
	}
	void inorder_tra(BTree_node* node)
	{
		if (!node)
			return;
		inorder_tra(node->left);
		cout << node->date;
		inorder_tra(node->right);
	}
	void postorder_tra(BTree_node* node)
	{
		if (!node)
			return;
		postorder_tra(node->left);
		postorder_tra(node->right);
		cout << node->date;
	}
	void createTree(BTree_node*& node) {
		char ch;
		cin >> ch;
		if ('#' == ch) {
			node = NULL;
			return;
		}
		node = new BTree_node;
		node->set(ch);
		createTree(node->left);
		createTree(node->right);
	}
	void del_tree(BTree_node* node) {
		if (!node) {
			delete node;
			return;
		}
		del_tree(node->left);
		del_tree(node->right);
		delete node;
	}
public:
	BTree() { root = NULL; }
	void createTree() { createTree(root); }
	void preorder_tra() { preorder_tra(root); cout << endl; }
	void inorder_tra() { inorder_tra(root); cout << endl; }
	void postorder_tra() { postorder_tra(root); cout << endl; }
	~BTree() { del_tree(root); }
};


int main() {
	int n;
	cin >> n;
	while (n--) {
		BTree b;
		b.createTree();
		b.preorder_tra();
		b.inorder_tra();
		b.postorder_tra();
	}
	return 0;
}

问题 B: DS二叉树——二叉树之数组存储

题目描述

二叉树可以采用数组的方法进行存储，把数组中的数据依次自上而下,自左至右存储到二叉树结点中，一般二叉树与完全二叉树对比，比完全二叉树缺少的结点就在数组中用0来表示。，如下图所示
从上图可以看出，右边的是一颗普通的二叉树，当它与左边的完全二叉树对比，发现它比完全二叉树少了第5号结点，所以在数组中用0表示，同样它还少了完全二叉树中的第10、11号结点，所以在数组中也用0表示。

结点存储的数据均为非负整数

输入

第一行输入一个整数t，表示有t个二叉树

第二行起，每行输入一个数组，先输入数组长度，再输入数组内数据，每个数据之间用空格隔开，输入的数据都是非负整数

连续输入t行

输出

每行输出一个示例的先序遍历结果，每个结点之间用空格隔开

样例输入

3
3 1 2 3
5 1 2 3 0 4
13 1 2 3 4 0 5 6 7 8 0 0 9 10

样例输出

1 2 3
1 2 4 3
1 2 4 7 8 3 5 9 10 6

提示

注意从数组位置和二叉树深度、结点位置进行关联，或者父子结点在数组中的位置存在某种管理，例如i, i+1, i/2, i+1/2…或者2i, 2i+1…仔细观察哦

AC代码

#include
using namespace std;

class bTree {
	vector<int>node;
	void preorder(int index) {
		if (index >= node.size())
			return;
		if (node[index])
			cout << node[index] << " ";
		preorder(2 * index + 1);
		preorder(2 * index + 2);
	}
public:
	bTree() {
		int n;
		cin >> n;
		node.resize(n);
		for (int i = 0; i < n; i++)
			cin >> node[i];
	}
	void preorder() { preorder(0); cout << endl; }
};

int main() {
	int n;
	cin >> n;
	while (n--)
	{
		bTree b;
		b.preorder();
	}
	return 0;
}

问题 C: DS二叉树–叶子数量

题目描述

计算一颗二叉树包含的叶子结点数量。

提示：叶子是指它的左右孩子为空。

建树方法采用“先序遍历+空树用0表示”的方法，即给定一颗二叉树的先序遍历的结果为AB0C00D00，其中空节点用字符‘0’表示。则该树的逻辑结构如下图。

输入

第一行输入一个整数t，表示有t个测试数据

第二行起输入二叉树先序遍历的结果，空树用字符‘0’表示，输入t行

输出

逐行输出每个二叉树的包含的叶子数量

样例输入

3
AB0C00D00
AB00C00
ABC00D00E00

样例输出

2
2
3

AC代码

#include
using namespace std;

int main() {
	int n;
	cin >> n;
	while (n--)
	{
		string s;
		cin >> s;
		int index = 0;
		int cnt = 0;
		while (index < (int)s.length() - 2)
		{

			if (s[index] != '0' && s[index + 1] == '0' && s[index + 2] == '0')
			{
				index += 2;
				cnt++;
			}
			else index++;
		}
		cout << cnt << endl;
	}
	return 0;
}

问题 D: DS二叉树–左叶子数量

题目描述

计算一颗二叉树包含的叶子结点数量。

左叶子是指它的左右孩子为空，而且它是父亲的左孩子

提示：可以用三叉链表法，也可以用现有算法对两层结点进行判断

建树方法采用“先序遍历+空树用0表示”的方法

输入

第一行输入一个整数t，表示有t个测试数据

第二行起输入二叉树先序遍历的结果，空树用字符‘0’表示，输入t行

输出

逐行输出每个二叉树的包含的左叶子数量

样例输入

3
AB0C00D00
AB00C00
ABCD0000EF000

样例输出

0
1
2

AC代码

#include
using namespace std;

struct BTree_node
{
	char date;
	BTree_node* left, * right;
	void set(char c, BTree_node* l = NULL, BTree_node* r = NULL) { date = c; left = l; right = r; }
};

class BTree {
	BTree_node* root;
	void preorder_tra(BTree_node* node, int& cnt) {
		if (!node)
			return;
		//cout << node->date;
		if (node->left && node->left->left == NULL && node->left->right == NULL)
			cnt++;
		preorder_tra(node->left, cnt);
		preorder_tra(node->right, cnt);
	}
	void inorder_tra(BTree_node* node)
	{
		if (!node)
			return;
		inorder_tra(node->left);
		cout << node->date;
		inorder_tra(node->right);
	}
	void postorder_tra(BTree_node* node)
	{
		if (!node)
			return;
		postorder_tra(node->left);
		postorder_tra(node->right);
		cout << node->date;
	}
	void createTree(BTree_node*& node) {
		char ch;
		cin >> ch;
		if ('0' == ch) {
			node = NULL;
			return;
		}
		node = new BTree_node;
		node->set(ch);
		createTree(node->left);
		createTree(node->right);
	}
	void del_tree(BTree_node* node) {
		if (!node) {
			delete node;
			return;
		}
		del_tree(node->left);
		del_tree(node->right);
		delete node;
	}
public:
	BTree() { root = NULL; }
	void createTree() { createTree(root); }
	void preorder_tra() { int cnt = 0; preorder_tra(root, cnt); cout << cnt << endl; }
	void inorder_tra() { inorder_tra(root); cout << endl; }
	void postorder_tra() { postorder_tra(root); cout << endl; }
	~BTree() { del_tree(root); }
	void levelorder() {
		queue<BTree_node*>q;
		q.push(root);
		while (!q.empty()) {
			BTree_node* cur_node = q.front();
			q.pop();
			if (cur_node == NULL)
				continue;
			cout << cur_node->date;
			//if (cur_node->left)
			q.push(cur_node->left);
			//if (cur_node->right)
			q.push(cur_node->right);
		}
		cout << endl;
	}
};


int main() {
	int n;
	cin >> n;
	while (n--) {
		BTree b;
		b.createTree();
		b.preorder_tra();
		//b.inorder_tra();
		//b.postorder_tra();
		//b.levelorder();
	}
	return 0;
}

问题 E: DS二叉树–层次遍历

题目描述

层次遍历二叉树，是从根结点开始遍历，按层次次序“自上而下，从左至右”访问树中的各结点。

建树方法采用“先序遍历+空树用0表示”的方法

要求：采用队列对象实现，函数框架如下：

输入

第一行输入一个整数t，表示有t个测试数据

第二行起输入二叉树先序遍历的结果，空树用字符‘0’表示，输入t行

输出

逐行输出每个二叉树的层次遍历结果

样例输入

2
AB0C00D00
ABCD00E000FG00H0I00

样例输出

ABDC
ABFCGHDEI

AC代码

#include
using namespace std;

struct BTree_node
{
	char date;
	BTree_node* left, * right;
	void set(char c, BTree_node* l = NULL, BTree_node* r = NULL) { date = c; left = l; right = r; }
};

class BTree {
	BTree_node* root;
	void preorder_tra(BTree_node* node) {
		if (!node)
			return;
		cout << node->date;
		preorder_tra(node->left);
		preorder_tra(node->right);
	}
	void inorder_tra(BTree_node* node)
	{
		if (!node)
			return;
		inorder_tra(node->left);
		cout << node->date;
		inorder_tra(node->right);
	}
	void postorder_tra(BTree_node* node)
	{
		if (!node)
			return;
		postorder_tra(node->left);
		postorder_tra(node->right);
		cout << node->date;
	}
	void createTree(BTree_node*& node) {
		char ch;
		cin >> ch;
		if ('0' == ch) {
			node = NULL;
			return;
		}
		node = new BTree_node;
		node->set(ch);
		createTree(node->left);
		createTree(node->right);
	}
	void del_tree(BTree_node* node) {
		if (!node) {
			delete node;
			return;
		}
		del_tree(node->left);
		del_tree(node->right);
		delete node;
	}
public:
	BTree() { root = NULL; }
	void createTree() { createTree(root); }
	void preorder_tra() { preorder_tra(root); cout << endl; }
	void inorder_tra() { inorder_tra(root); cout << endl; }
	void postorder_tra() { postorder_tra(root); cout << endl; }
	~BTree() { del_tree(root); }
	void levelorder() {
		queue<BTree_node*>q;
		q.push(root);
		while (!q.empty()) {
			BTree_node* cur_node = q.front();
			q.pop();
			if (cur_node == NULL)
				continue;
			cout << cur_node->date;
			//if (cur_node->left)
			q.push(cur_node->left);
			//if (cur_node->right)
			q.push(cur_node->right);
		}
		cout << endl;
	}
};


int main() {
	int n;
	cin >> n;
	while (n--) {
		BTree b;
		b.createTree();
		//b.preorder_tra();
		//b.inorder_tra();
		//b.postorder_tra();
		b.levelorder();
	}
	return 0;
}

问题 F: DS二叉树–后序遍历非递归算法

题目描述

求一颗树的后序遍历的非递归算法
要求：必须是非递归算法，使用堆栈对象来实现
建树方法采用“先序遍历+空树用0表示”的方法
算法流程：

输入

第一行输入一个整数t，表示有t个测试数据

第二行起输入二叉树先序遍历的结果，空树用字符‘0’表示，输入t行

输出

逐行输出每个二叉树的后序遍历结果

样例输入

3
AB0C00D00
ABC00D00EF000
ABCD0000E0F00

样例输出

CBDA
CDBFEA
DCBFEA

AC代码

#include
using namespace std;

struct BTree_node
{
	char date;
	BTree_node* left, * right;
	void set(char c, BTree_node* l = NULL, BTree_node* r = NULL) { date = c; left = l; right = r; }
};

class BTree {
	BTree_node* root;
	void preorder_tra(BTree_node* node) {
		if (!node)
			return;
		if (!node->left && !node->right)
			cout << node->date << " ";
		preorder_tra(node->left);
		preorder_tra(node->right);
	}
	void fparent(BTree_node* node) {
		if (!node)
			return;
		fparent(node->left);
		fparent(node->right);
		if ((node->left && !node->left->left && !node->left->right))
			cout << node->date << " ";
		if (node->right && !node->right->left && !node->right->right)
			cout << node->date << " ";
	}

	void inorder_tra(BTree_node* node)
	{
		if (!node)
			return;
		inorder_tra(node->left);
		cout << node->date;
		inorder_tra(node->right);
	}
	void postorder_tra(BTree_node* node)
	{
		if (!node)
			return;
		postorder_tra(node->left);
		postorder_tra(node->right);
		cout << node->date;
	}
	void createTree(BTree_node*& node) {
		char ch;
		cin >> ch;
		if ('0' == ch) {
			node = NULL;
			return;
		}
		node = new BTree_node;
		node->set(ch);
		createTree(node->left);
		createTree(node->right);
	}
	void del_tree(BTree_node* node) {
		if (!node) {
			delete node;
			return;
		}
		del_tree(node->left);
		del_tree(node->right);
		delete node;
	}
public:
	BTree() { root = NULL; }
	void createTree() { createTree(root); }
	void preorder_tra() { preorder_tra(root); cout << endl; }
	void fparent() { fparent(root); cout << endl; }
	void inorder_tra() { inorder_tra(root); cout << endl; }
	void postorder_tra() { postorder_tra(root); cout << endl; }
	~BTree() { del_tree(root); }
	void postorder1() { 
		BTree_node* cur_node = root;
		stack<BTree_node*> search_queue;
		stack<bool> state;
		do {
			if (NULL!=cur_node) {
				search_queue.push(cur_node);
				state.push(0);
				cur_node = cur_node->left;
				continue;
			}

			if (!state.top()) {
				state.top() = 1;
				cur_node = search_queue.top()->right;
			}
			else {
				cout << search_queue.top()->date;
				search_queue.pop();
				state.pop();
				cur_node = NULL;
			}

		} while (!search_queue.empty());
		cout << endl;
	}
};


int main() {
	int n;
	cin >> n;
	while (n--) {
		BTree b;
		b.createTree();
		/*b.preorder_tra();
		b.fparent();*/
		//b.inorder_tra();
		//b.postorder_tra();
		b.postorder1();
	}
	return 0;
}

问题 G: DS二叉树——二叉树之父子结点

题目描述

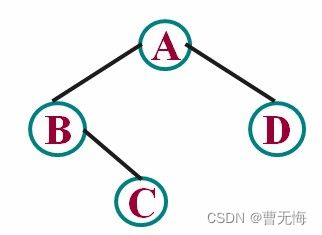
给定一颗二叉树的逻辑结构如下图，（先序遍历的结果，空树用字符‘0’表示，例如AB0C00D00），建立该二叉树的二叉链式存储结构。

编写程序输出该树的所有叶子结点和它们的父亲结点

输入

第一行输入一个整数t，表示有t个二叉树

第二行起，按照题目表示的输入方法，输入每个二叉树的先序遍历，连续输入t行

输出

第一行按先序遍历，输出第1个示例的叶子节点

第二行输出第1个示例中与叶子相对应的父亲节点

以此类推输出其它示例的结果

样例输入

3
AB0C00D00
AB00C00
ABCD0000EF000

样例输出

C D
B A
B C
A A
D F
C E

AC代码

#include
using namespace std;

struct BTree_node
{
	char date;
	BTree_node* left, * right;
	void set(char c, BTree_node* l = NULL, BTree_node* r = NULL) { date = c; left = l; right = r; }
};

class BTree {
	BTree_node* root;
	void preorder_tra(BTree_node* node) {
		if (!node)
			return;
		if (!node->left && !node->right)
			cout << node->date << " ";
		preorder_tra(node->left);
		preorder_tra(node->right);
	}
	void fparent(BTree_node* node) {
		if (!node)
			return;
		fparent(node->left);
		fparent(node->right);
		if ((node->left && !node->left->left && !node->left->right))
			cout << node->date << " ";
		if (node->right && !node->right->left && !node->right->right)
			cout << node->date << " ";
	}

	void inorder_tra(BTree_node* node)
	{
		if (!node)
			return;
		inorder_tra(node->left);
		cout << node->date;
		inorder_tra(node->right);
	}
	void postorder_tra(BTree_node* node)
	{
		if (!node)
			return;
		postorder_tra(node->left);
		postorder_tra(node->right);
		cout << node->date;
	}
	void createTree(BTree_node*& node) {
		char ch;
		cin >> ch;
		if ('0' == ch) {
			node = NULL;
			return;
		}
		node = new BTree_node;
		node->set(ch);
		createTree(node->left);
		createTree(node->right);
	}
	void del_tree(BTree_node* node) {
		if (!node) {
			delete node;
			return;
		}
		del_tree(node->left);
		del_tree(node->right);
		delete node;
	}
public:
	BTree() { root = NULL; }
	void createTree() { createTree(root); }
	void preorder_tra() { preorder_tra(root); cout << endl; }
	void fparent() { fparent(root); cout << endl; }
	void inorder_tra() { inorder_tra(root); cout << endl; }
	void postorder_tra() { postorder_tra(root); cout << endl; }
	~BTree() { del_tree(root); }
};


int main() {
	int n;
	cin >> n;
	while (n--) {
		BTree b;
		b.createTree();
		b.preorder_tra();
		b.fparent();
		//b.inorder_tra();
		//b.postorder_tra();
	}
	return 0;
}