C语言-操作符详解
编程不仅仅是关于写代码,它也涉及到了解代码背后的基础概念。操作符在告诉计算机我们想要它执行什么操作方面起着至关重要的作用。本篇博客将深入探讨不同类型的操作符以及它们的用途。
一、操作符的分类
二、二进制和进制转换
⽐如:数值15的各种进制的表⽰形式:15的2进制:111115的8进制:1715的10进制:1515的16进制:F
二进制是计算机科学和数字电子学中最基础的数制,因为它只使用两个不同的数字:0和1。每一个二进制位(bit)代表了2的幂次,在计算机中,它们是数据和指令的基本构建块。
1.原理
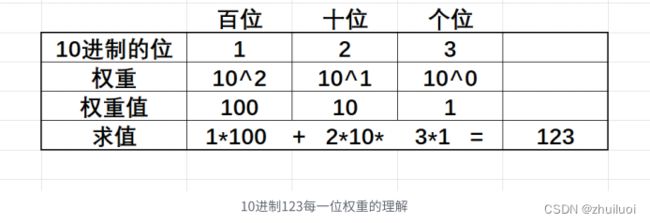
二进制的工作原理基于位权的概念,类似于我们熟悉的十进制系统。在十进制系统中,每一位的位权是10的幂次,例如:
- 个位(
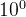 )
) - 十位(
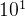 )
) - 百位(
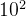 )
)
相应的,二进制的位权是2的幂次:
- 最右边的位(最低位)是

- 然后是
 ,
, ,以此类推
,以此类推
10进制中满10进1
10进制的数字每⼀位都是0~9的数字组成
2进制中满2进12进制的数字每⼀位都是0~1的数字组成
2. 为什么使用二进制
计算机使用二进制是因为它们通过电路来处理信息,而电路有两个明显的状态:通电和断电,这自然对应于1和0。使用二进制,计算机可以简单地通过开关状态来表示和存储数据。
3. 二进制与计算机硬件
在硬件层面,RAM(随机存取存储器)、CPU(中央处理单元)、GPU(图形处理单元)等都是通过二进制来存储和处理信息的。比如,一个位可以表示一个简单的是/否或者开/关状态;8位可以组成一个字节(byte),可以表示256种(2828)不同的状态或者值。
4. 二进制数的读写
(1)2进制转10进制
阅读二进制和写二进制都是基于上述位权原理。例如,二进制数1011表示为十进制是:
- 1×
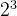 (8)
(8) - 0×
 (0)
(0) - 1×
 (2)
(2) - 1×
 (1)
(1)
相加就得到十进制数11。
(2)10进制转2进制数字
将十进制数字转换为二进制主要使用了“除2取余法”,即不断地将十进制数字除以2,并记录下每次除法操作后的余数,直到商为0为止。然后,将所有的余数倒序排列,这个倒序排列后的序列就是对应的二进制数。
以下是一个具体的转换步骤示例,我们以十进制数29转换为二进制数为例:
- 29 ÷ 2 = 14 余 1
- 14 ÷ 2 = 7 余 0
- 7 ÷ 2 = 3 余 1
- 3 ÷ 2 = 1 余 1
- 1 ÷ 2 = 0 余 1
然后将得到的余数从下到上倒序排列,得到:11101。
因此,十进制的29转换为二进制就是11101。
我们再来看一个更简单的例子,将十进制数5转换为二进制数:
- 5 ÷ 2 = 2 余 1
- 2 ÷ 2 = 1 余 0
- 1 ÷ 2 = 0 余 1
倒序排列余数得到:101。
因此,十进制的5转换为二进制就是101。
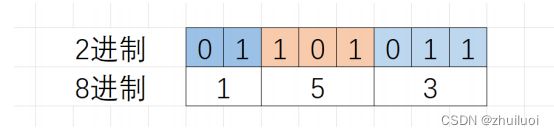
(3)2进制转8进制
如:2进制的01101011,换成8进制:0153,0开头的数字,会被当做8进制。
(4)2进制转16进制
如:2进制的01101011,换成16进制:0x6b,16进制表⽰的时候前⾯加0x
三、原码、反码、补码
原码、反码、补码是在计算机系统中用于表示有符号数值的三种不同形式,主要用于二进制数的表示和运算。它们的定义和转换在计算机科学特别是在位运算和算术运算的上下文中非常重要。
整数的2进制表⽰⽅法有三种,即原码、反码和补码有符号整数的三种表示⽅法均有符号位和数值位两部分,2进制序列中,最⾼位的1位是被当做符号位,剩余的都是数值位。符号位都是⽤0表示“正”,用1表示“负”。
1. 原码
原码是最直观的二进制数表示方式,用于表示带符号的二进制数。在原码表示法中,最左边的位用作符号位,通常是0表示正数,1表示负数。其余位表示数值的绝对值。
例如,用一个字节表示(假设在8位计算机架构中):
- +9 的原码:00001001
- -9 的原码:10001001
2. 反码
反码是将原码的数值位取反得到的。对于正数,反码与原码相同;对于负数,除了符号位保持不变,其余各位都取反。
以+9和-9为例,其反码表示如下:
- +9 的反码:00001001 (与原码相同)
- -9 的反码:11110110 (数值位取反)
3. 补码
补码是现代计算机中最常用的方式来表示有符号整数的。它解决了原码和反码表示法中的一些问题,例如在原码和反码中,+0和-0有两种表示,而在补码中只有一种。补码也简化了加法和减法运算。
补码是通过将原码取反(得到反码)后加1得到的。对于正数,补码与原码相同;对于负数,是其反码的基础上加1。
以+9和-9为例,其补码表示如下:
- +9 的补码:00001001 (与原码相同)
- -9 的补码:11110111 (反码11110110 + 1)
4. 为什么使用补码
补码的使用允许更简单的算术运算和更有效的硬件实现。它让加法和减法运算可以统一处理,无需为正数和负数分别设计电路。例如,在补码系统中,如果你想做减法,你可以简单地将一个数的补码加到另一个数上。
总结一下,原码是最直观的表示,反码是对原码除符号位外的取反,补码则是在反码的基础上加1。补码的普遍应用是由于它在计算机运算中的优势,特别是在执行算术运算时。
正整数的原、反、补码都相同。负整数的三种表示方法各不相同。原码:直接将数值按照正负数的形式翻译成⼆进制得到的就是原码。反码:将原码的符号位不变,其他位依次按位取反就可以得到反码。补码:反码+1就得到补码。补码得到原码也是可以使用:取反,+1的操作。
四、移位操作符
<<:左移位操作,按指定位数将一个数的所有位向左移动>>:右移位操作,按指定位数将一个数的所有位向右移动
注:移位操作符的操作数只能是整数。
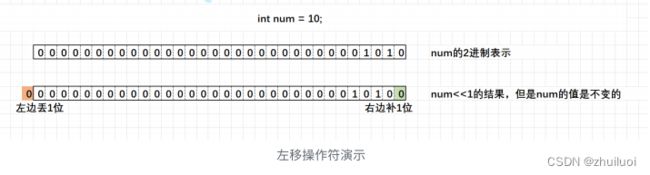
1. 左移操作符
#include
int main()
{
int num = 10;
int n = num<<1;
printf("n= %d\n", n);
printf("num= %d\n", num);
return 0;
} 2. 右移操作符
- 逻辑右移:左边⽤0填充,右边丢弃
- 算术右移:左边⽤原该值的符号位填充,右边丢弃
#include
int main()
{
int num = 10;
int n = num>>1;
printf("n= %d\n", n);
printf("num= %d\n", num);
return 0;
} 五、位操作符
&:按位与|:按位或^:按位异或
注:他们的操作数必须是整数。
#include
int main()
{
int num1 = -3;
int num2 = 5;
printf("%d\n", num1 & num2);
printf("%d\n", num1 | num2);
printf("%d\n", num1 ^ num2);
printf("%d\n", ~0);
return 0;
} 六、单目操作符
!:逻辑非++:自增--:自减&:取地址*:解引用+:正号-:负号~:按位取反sizeof:大小,返回数据类型或对象所占空间大小(类型):类型转换
七、逗号表达式
,:逗号操作符用于分隔表达式,并按顺序执行它们。
int a = 1;
int b = 2;
int c = (a>b, a=b+10, a, b=a+1);//逗号表达式 c是多少?这里的逗号操作符将会执行以下操作:
a>b:比较a和b的值,由于a不大于b,此表达式的结果是false(在C语言中通常用0表示),但这个结果被逗号操作符丢弃。a=b+10:将b的值加10赋给a,因此a现在变为12。a:简单地评估a的值,结果为12,但这个结果也被逗号操作符丢弃。b=a+1:将a的值加1赋给b,因此b现在变为13。最后一个表达式
b=a+1的结果是13,这是整个逗号表达式的值,因此变量c的最终值为13。
八、下标访问[]、函数调用()
1. 下标引用
[ ]:数组下标操作符,用于访问数组中的元素。
int arr[10];//创建数组
arr[9] = 10;//实⽤下标引⽤操作符。
[ ]的两个操作数是arr和9。2.函数调用
( ):函数调用操作符,用于调用函数。
#include
void test1()
{
printf("hehe\n");
}
void test2(const char *str)
{
printf("%s\n", str);
}
int main()
{
test1(); //这⾥的()就是作为函数调⽤操作符。
test2("hello bit.");//这⾥的()就是函数调⽤操作符。
return 0;
} 九、结构成员访问
1. 结构体
C语⾔已经提供了内置类型,如:char、short、int、long、float、double等,但是只有这些内置类型还是不够的,假设我想描述学⽣,描述⼀本书,这时单⼀的内置类型是不⾏的。描述⼀个学⽣需要名字、年龄、学号、⾝⾼、体重等;描述⼀本书需要作者、出版社、定价等。C语⾔为了解决这个问题,增加了结构体这种⾃定义的数据类型,让程序员可以⾃⼰创造适合的类型。
在编程中,特别是在C语言或C++中,结构体(Structures)是一种创建自己的数据类型的方式。结构体允许你将多个变量合并为一个单独的复合数据类型,这些变量(称为成员)可以是不同的数据类型。
(1)结构体的定义
结构体的定义以关键字 struct 开始,后跟结构体的名称和花括号内的成员列表,最后以分号结束。例如:
struct Person {
char name[50];
int age;
float salary;
};在这个例子中,Person 结构体有三个成员:一个字符数组 name,一个整型 age 和一个浮点型 salary。
(2)创建结构体变量
定义了结构体类型之后,就可以使用它来创建变量:
struct Person person1;上面的代码创建了一个 Person 类型的变量 person1。
2. 访问结构体成员
你可以使用点操作符(.)来访问结构体的成员:
strcpy(person1.name, "Alice");
person1.age = 30;
person1.salary = 58000.50;结构体指针
如果有一个指向结构体的指针,你需要使用箭头操作符(->)来访问结构体的成员:
struct Person *ptr = &person1;
ptr->age = 30; // 等同于 person1.age = 30;结构体作为函数参数
结构体可以作为函数的参数传递,传递方式可以是值传递也可以是引用传递(通常使用指针来避免结构体的复制,节省内存和时间)。
void printPerson(struct Person p) {
printf("Name: %s\n", p.name);
printf("Age: %d\n", p.age);
printf("Salary: %.2f\n", p.salary);
}
printPerson(person1); // 通过值传递结构体结构体数组
就像其他类型的数组一样,也可以创建结构体数组:
struct Person employees[5];这里创建了一个包含5个 Person 结构体的数组 employees。
3. typedef 和结构体
typedef 可以用来给结构体类型起一个新名字,使得在代码中不必重复使用 struct 关键字:
typedef struct Person {
char name[50];
int age;
float salary;
} Person;
Person person4;现在,Person 既是结构体的名称,也是该类型的新别名。可以直接使用 Person person4; 来定义一个新的结构体变量。
十、操作符的属性:优先级、结合性
在编程中,特别是在C、C++、Java和类似的语言中,每个操作符都有两个基本的属性:优先级和结合性。这些属性决定了复杂表达式中操作符的执行顺序。
1. 优先级(Precedence)
操作符的优先级决定了当表达式中有多个不同操作符时,哪些操作符会先被计算。优先级高的操作符会先被执行。比如,在表达式 3 + 4 * 5 中,乘法操作符(*)的优先级高于加法(+),因此先计算 4 * 5,然后将结果加到 3 上。
操作符的优先级是由语言的规范定义的,并且在大多数语言中,算术操作符的优先级高于比较操作符,比较操作符又高于逻辑操作符。例如,在C和C++中,* 和 / 的优先级高于 + 和 -。
2. 结合性(Associativity)
结合性决定了当表达式中有多个相同优先级的操作符时,它们的执行顺序。大多数操作符有左结合性,意味着这些操作符会从左到右顺序执行。例如,表达式 100 / 10 / 2 从左到右计算,先计算 100 / 10 得到 10,然后用 10 除以 2,结果为 5。
然而,也有一些操作符是右结合的,最典型的是赋值操作符(=)。在表达式 a = b = 5 中,先计算 b = 5,然后将 b 的新值赋给 a。
3. 示例
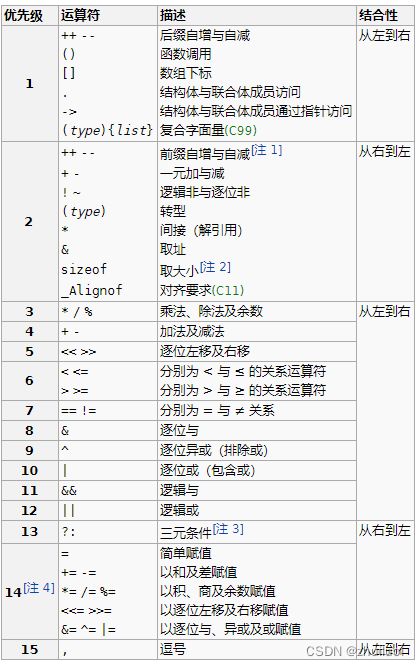
以C语言中的操作符为例,以下是一些常见操作符及其优先级和结合性:
- 操作符
()、[]、.、->有最高的优先级,左结合性。 - 单目操作符如
++、--、!、~紧随其后,有右结合性。 - 算术操作符
*、/、%的优先级高于+、-,都是左结合性。 - 关系操作符
>、<、>=、<=的优先级高于等于操作符==、!=,所有这些都是左结合性。 - 位操作符
&、^、|通常优先级较低,左结合性。 - 逻辑操作符
&&、||的优先级更低,左结合性。 - 赋值操作符
=、+=、-=等的优先级几乎是最低的,且是右结合的。 - 逗号操作符
,有最低的优先级,左结合性。
- 圆括号( ( ) )
为了正确理解和使用操作符,特别是在编写复杂的表达式时,了解每个操作符的优先级和结合性是非常重要的。
4. 表达式求值
使用优先级和结合性规则,我们可以不使用任何括号来计算复杂表达式的值。然而,为了提高可读性和避免错误,推荐在可能产生歧义的地方使用括号来明确指定操作的顺序。
(1)整型提升
整型提升(Integer Promotion)是编程语言中的一个概念,尤其是在C和C++语言中。它涉及到在表达式求值时,较小的整型数据(如 char 和 short)自动转换为较大的整型数据(通常是 int 或 unsigned int),以便进行算术运算。
整型提升发生的情况包括:
在运算中:当较小的整型数据类型参与运算时,例如与 int 类型一起,在执行运算之前,这些较小的数据类型会被提升为 int 类型。这是为了减少由于类型较小而可能导致的溢出问题,并且提高运算速度,因为大多数现代处理器都是优化来处理 int 大小的数据的。
函数参数传递:在C语言中,当函数的原型未被明确声明或者使用了变长参数列表时,比如使用 ...(如 printf 和 scanf 函数),较小的整型参数会被提升为 int 类型。
整型提升的规则如下:
char、signed char、unsigned char、short int和unsigned short int类型的值在参与表达式运算时,通常会被提升到int或unsigned int。- 如果
int能够表示所有可能的值,那么unsigned char或unsigned short int在表达式中会被提升到int。 - 如果
int不能表示所有的unsigned char或unsigned short int的值(例如,int是16位而unsigned short int也是16位),那么这些类型将被提升到unsigned int。 - 已经是
int或更大整数类型的值不会被提升。
举个例子:
char a = 10;
char b = 20;
int c = a + b;
在这个例子中,a 和 b 都是 char 类型的变量。在执行 a + b 运算时,a 和 b 的值首先被提升到 int 类型,然后进行加法运算,最后的结果赋给 int 类型的变量 c。
整型提升是自动发生的,编程时通常不需要程序员明确指出。然而,了解它的存在是很重要的,因为它可以影响程序中数值计算的结果。
如何进⾏整体提升呢?
1. 有符号整数提升是按照变量的数据类型的符号位来提升的2. ⽆符号整数提升,⾼位补0
//负数的整形提升
char c1 = -1; 变量c1的⼆进制位(补码)中只有8个⽐特位:
1111111
因为 char 为有符号的 char
所以整形提升的时候,⾼位补充符号位,即为1 提升之后的结果是:
11111111111111111111111111111111
//正数的整形提升
char c2 = 1; 变量c2的⼆进制位(补码)中只有8个⽐特位:
00000001
因为 char 为有符号的 char
所以整形提升的时候,⾼位补充符号位,即为0 提升之后的结果是:
00000000000000000000000000000001
//⽆符号整形提升,⾼位补0(2)算术转换
算术转换是编程中的一个概念,它指的是在执行算术运算时,如何将操作数转换为适当的共同类型以保证运算的正确性。这个过程也称为“寻常算术转换”(usual arithmetic conversions)。其目的是为了使运算符可以应用于多种类型的操作数,并得到一个合理的结果。
在C和C++语言中,这一过程遵循以下几个步骤:
-
整型提升:首先,所有小于
int类型的整型值都会提升到int或unsigned int。 -
无符号规则:如果一个操作数是无符号的,而另一个操作数具有相同或较小的类型,则较小的类型(或相同类型的有符号类型)将被转换为相应的无符号类型。
-
类型兼容性:如果操作数的类型不同,则转换会发生在较小的类型上,使其与较大的类型兼容。通常,较小的类型会转换为较大的类型。转换遵循以下的类型排列顺序(从低到高):
charshortintunsigned intlongunsigned longlong longunsigned long longfloatdoublelong double
-
浮点提升:如果任一操作数是浮点类型(
float、double或long double),则整数操作数将被转换为浮点类型。
例如,如果你有一个int类型和一个float类型的操作数,int会被转换为float,然后执行运算。这样保证了运算结果为float类型。
一个具体的例子:
int i = 5;
float f = 2.5;
double d = 3.5;
// i 提升为 float,然后与 f 相加,结果为 float
float result1 = i + f;
// result1 是 float,提升为 double,然后与 d 相加,结果为 double
double result2 = result1 + d;在这个例子中,首先int的i被提升为float,然后执行加法运算。在第二个表达式中,float的result1被提升为double,然后与double的d相加。
这些隐式转换在编写表达式时非常有用,因为它们允许不同类型的操作数在不必显式转换的情况下一起工作。然而,这也可能导致一些不明显的问题,比如精度丢失或溢出,尤其是涉及无符号整数时。因此,了解这些规则是非常重要的。